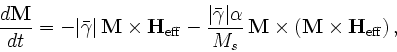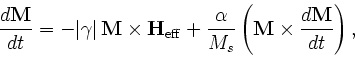- Specify Oxs_BoxAtlas:atlasname {
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- name regionname
- }
where xmin, xmax, ... are coordinates in meters, specifying the extents of the volume being defined. The regionname label specifies the name assigned to the region contained in the atlas. The name entry is optional; if not specified then the region name is taken from the object instance name, i.e., atlasname.
For situations requiring continuous variation in material parameters, the script field classes should be used in conjunction with the ReadFile MIF extension command. See the ColorField sample proc in the ReadFile documentation for an example of this technique.
The Oxs_ImageAtlas Specify block has the following form:
- Specify Oxs_ImageAtlas:name {
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- viewplane view
- image pic
- colormap {
}
- color-1 region_name
- color-2 region_name
- ...
- color-n region_name
- matcherror max_color_distance
- }
The xrange, yrange, zrange entries specify the extent of the atlas, in meters. The viewplane view value should be one of the 3 two-letter codes xy, zx or yz, which specify the mapping of the horizontal and vertical axes of the image respectively to axes in the simulation. The image is scaled as necessary along each dimension to match the atlas extents along the corresponding axes. The image is overlaid through the entire depth of the perpendicular dimension, i.e., along the axis absent from the viewplane specification. The Oxs_ImageAtlas class can be used inside a Oxs_MultiAtlas object to specify regions in a multilayer structure.
The image entry specifies the name of the image file to use. If the file path is relative, then it will be taken with respect to the directory containing the MIF file. The image format may be any of those recognized by any2ppm. The file will be read directly by Oxs if it is in the P3 or P6 PPM formats, otherwise any2ppm will be automatically launched to perform the conversion.
The colormap value is an even length list of color + region name pairs. The colors may be specified in any of several ways. The most explicit is to use one of the Tk numeric formats, #rgb, #rrggbb, #rrrgggbbb or #rrrrggggbbbb, where each r, g, and b is one hex digit (i.e., 0-9 or A-F) representing the red, green and blue components of the color, respectively. For example, #F00 is bright (full-scale) red, #800 would be a darker red, while #FF0 and #FFFF00 would both be bright yellow. Refer to the Tk_GetColor documentation for details. For shades of gray the special notation grayD or greyD is available, where D is a decimal value between 0 and 100, e.g., grey0 is black and grey100 is white. Alternatively, one may use any of the symbolic names defined in the oommf/config/colors.def file, such as red, white and skyblue. When comparing symbolic names, spaces and capitalization are ignored. The list of symbolic names can be extended by adding additional files to the Color filename option in the options.tcl customization file. Finally, one color in the colormap list may optionally be the special keyword ``default,'' which essentially represents all colors not in the colormap list.
Each of the specified colors should be distinct, but the region names are allowed to be repeated as desired. The region names may be chosen arbitrarily, except the special keyword ``universe'' is reserved for points not in any of the regions. This includes all points outside the atlas bounding box defined by the xrange, yrange, zrange entries, but may also include points inside that boundary.
Pixels in the image are assigned to regions by comparing the color of the pixel to the list of colors specified in colormap. If the pixel color is closer to a colormap color than max_color_distance, then the colors are considered matched. If a pixel color matches exactly one colormap color, then the pixel is assigned to the corresponding region. If a pixel color matches more than one colormap color, the pixel is assigned to the region corresponding to the closest match. If a pixel color doesn't match any of the colormap colors, then it is assigned to the default region, which is the region paired with the ``default'' keyword. If default does not explicitly appear in the colormap colors list, then universe is made the default region.
To calculate the distance between two colors, each color is first converted to a scaled triplet of floating point red, green, and blue values, (r, g, b), where each component lies in the interval [0, 1], with (0, 0, 0) representing black and (1, 1, 1) representing white. For example, (0, 0, 1) is bright blue. Given two colors in this representation, the distance is computed using the standard Euclidean norm with uniform weights, i.e., the distance between (r1, g1, b1) and (r2, g2, b2) and is
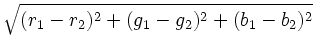 .
.
As explained above, two colors are considered to match if the distance
between them is less than the specified matcherror value. If
max_color_distance is sufficiently small, then it may easily
happen that a pixel's color does not match any of the specified region
colors, so the pixel would be assigned to the default region. On the
other hand, if max_color_distance is larger than
![]() , then all colors will match, and no pixels will be
assigned to the default region. If matcherror is not specified,
then the default value for max_color_distance is 3, which
means all colors match.
, then all colors will match, and no pixels will be
assigned to the default region. If matcherror is not specified,
then the default value for max_color_distance is 3, which
means all colors match.
The following example should help clarify these matters.
Specify Oxs_ImageAtlas:atlas {
xrange { 0 400e-9 }
yrange { 0 200e-9 }
zrange { 0 20e-9 }
image mypic.gif
viewplane "xy"
colormap {
blue cobalt
red permalloy
green universe
default cobalt
}
matcherror .1
}
Pixels with colors that are equidistant to and match more than one color in the colormap will be assigned to one of the closest color regions. The user should not rely on any particular selection, that is to say, the explicit matching procedure in this case is not defined.
The Oxs_MultiAtlas specify block has the form
- Specify Oxs_MultiAtlas:name {
- atlas atlas_1_spec
- atlas atlas_2_spec
- ...
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- }
Each atlas_spec may be either a reference to an atlas defined earlier and outside the current Specify block, or else an inline, embedded atlas definition. The bounding box xrange, yrange and zrange specifications are each optional. If not specified the corresponding range for the atlas bounding box is taken from the minimal bounding box containing all the sub-atlases.
If the atlases are not disjoint, then the regions as defined by an Oxs_MultiAtlas can be somewhat different from those of the individual component atlases. For example, suppose regionA is a rectangular region in atlasA with corner points (5,5,0) and (10,10,10), and regionB is a rectangular region in atlasB with corner points (0,0,0) and (10,10,10). When composed in the order atlasA, atlasB inside an Oxs_MultiAtlas, regionA reported by the Oxs_MultiAtlas will be the same as regionA reported by atlasA, but regionB as reported by the Oxs_MultiAtlas will be the ``L'' shaped volume of those points in atlasB's regionB not inside regionA. If the Oxs_MultiAtlas is constructed with atlasB first and atlasA second, then regionB as reported by the Oxs_MultiAtlas would agree with that reported by atlasB, but regionA would be empty.
NOTE: The attributes key label is not supported by this class.
- Specify Oxs_ScriptAtlas:name {
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- regions { rname_1 rname_2 ... rname_n }
- script_args { args_request }
- script Tcl_script
- }
Here xmin, xmax, ... are coordinates in meters, specifying the extents of the axes-parallel rectangular parallelepiped enclosing the total volume being identified. This volume is subdivided into n sub-regions, using the names as given in the regions list. The script is used to assign points to the various regions. Appended to the script are the arguments requested by script_args, in the manner explained in the User Defined Support Procedures section of the MIF 2.1 file format documentation. The value args_request should be a subset of {relpt rawpt minpt maxpt span }. If script_args is not specified, the default value relpt is used. When executed, the return value from the script should be an integer in the range 1 to n, indicating the user-defined region in which the point lies, or else 0 if the point is not in any of the n regions. Region index 0 is reserved for the implicit ``universe'' region, which is all-encompassing. The following example may help clarify the discussion:
proc Octs { cellsize x y z xmin ymin zmin xmax ymax zmax } {
global RegionArray
set xindex [expr {int(floor(($x-$xmin)/$cellsize))}]
set yindex [expr {int(floor(($y-$ymin)/$cellsize))}]
set zindex [expr {int(floor(($z-$zmin)/$cellsize))}]
set octant [expr {1+$xindex+2*$yindex+4*$zindex}]
if {$octant<1 || $octant>8} {
return 0
}
return $octant
}
Specify Oxs_ScriptAtlas:octant {
xrange {-20e-9 20e-9}
yrange {-20e-9 20e-9}
zrange {-20e-9 20e-9}
regions { VIII V VII VI IV I III II }
script_args { rawpt minpt maxpt }
script { Octs 20e-9 }
}
This atlas divides the rectangular volume between
(- 20, - 20, - 20) and
(20, 20, 20) (nm) into eight regions, corresponding to the standard
octants, I through VIII. The Octs Tcl procedure returns a
value between 1 and 8, with 1 corresponding to octant VIII and 8 to
octant II. The canonical octant ordering starts with I as the
+ x, + y, + z space, proceeds counterclockwise in the + z half-space, and
concludes in the - z half-space with V directly beneath I, VI beneath
II, etc. The ordering computed algorithmically in Octs
starts with 1 for the - x, - y, - z space, 2 for the + x, - y, - z space, 3
for the - x, + y, - z space, etc. The conversion between the two systems
is accomplished by the ordering of the regions list.

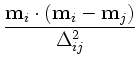
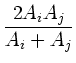 ,
,
![$\displaystyle {\frac{{\sigma\left[1-\textbf{m}_i\cdot\textbf{m}_j\right]
+\sig...
...\left[1-\left(\textbf{m}_i\cdot\textbf{m}_j\right)^2\right]
}}{{\Delta_{ij}}}}$](img12.gif)