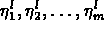 , where the subscripts
correspond to times
, where the subscripts
correspond to times 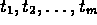 and the superscript
and the superscript
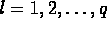 is the time series index.
Suppose that these data are to
be modeled by a system of
is the time series index.
Suppose that these data are to
be modeled by a system of 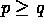 first order ODEs
first order ODEs
Bert W. Rust, ACMD
Robert W. Ashton, Chemical Science and Technology Laboratory
An important inverse problem in time series modeling is to fit a system of
ordinary differential equations (ODEs) to a set of observed time series
data which are corrupted by stochastic measuring errors.
Let the given data be one or more measured time series
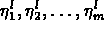 , where the subscripts
correspond to times
, where the subscripts
correspond to times 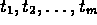 and the superscript
and the superscript
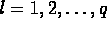 is the time series index.
Suppose that these data are to
be modeled by a system of
is the time series index.
Suppose that these data are to
be modeled by a system of 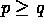 first order ODEs
first order ODEs
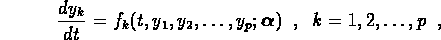
where q of the 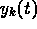 are to be fit to the
measured data, and
are to be fit to the
measured data, and
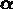 is an n-vector of parameter values to be determined by
fitting. If the initial measurements
is an n-vector of parameter values to be determined by
fitting. If the initial measurements 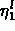 are corrupted by
measurement error, it
is necessary to also include the p-vector
are corrupted by
measurement error, it
is necessary to also include the p-vector 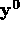 of initial
conditions
of initial
conditions
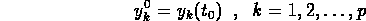
as fitting parameters in order not to bias the fit. In most cases the system of ODEs cannot be solved in closed form so it is necessary to combine a numerical integrator with parameter fitting program. This is accomplished by using David Kahaner's integrator SDRIV1 together with the Stanford nonlinear least squares code VARPRO to minimize
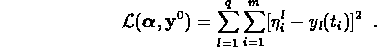
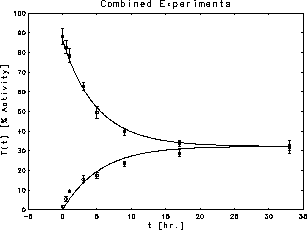
Figure 13: Simultaneous fits to the two thrombin
concentration time series
The least squares code also requires the partial derivatives of 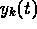 with respect to each of the fitting parameters. These can be computed
exactly by numerically integrating the system of variational equations
with respect to each of the fitting parameters. These can be computed
exactly by numerically integrating the system of variational equations
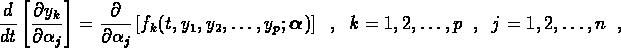
and
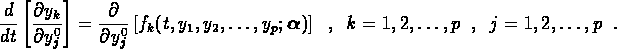
Since each of the 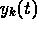 are implicit functions of all of the
are implicit functions of all of the 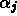 and all of the
and all of the 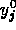 , the partial derivatives of the right hand sides
can become complicated and numerous.
, the partial derivatives of the right hand sides
can become complicated and numerous.
A recent biochemical application of this program at NIST arose in connection
with a study of the ability of anhydrothrombin (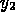 ), a derivative of the
enzyme thrombin (
), a derivative of the
enzyme thrombin (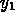 ), to compete with thrombin for the binding of a potent
thrombin inhibitor hirudin (
), to compete with thrombin for the binding of a potent
thrombin inhibitor hirudin (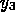 ). The system of ODEs describing the
kinetics of the reactions can be written
). The system of ODEs describing the
kinetics of the reactions can be written
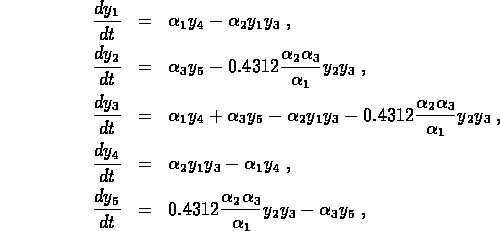
where 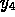 and
and 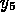 are the concentrations of the molecules
thrombin-hirudin complex and anhydrothrombin complex, respectively, and
are the concentrations of the molecules
thrombin-hirudin complex and anhydrothrombin complex, respectively, and
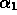 ,
, 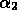 and
and 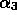 are parameters to be determined
by the fit. The initial values
are parameters to be determined
by the fit. The initial values 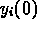 were known exactly so there were
only 15 variational equations for the partial derivatives
were known exactly so there were
only 15 variational equations for the partial derivatives
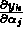 .
.
The measured data were two time series of thrombin concentrations,
corresponding to two separate experiments with different values of the initial
conditions 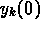 . If the concentrations are expressed in units of
%Activity, then one experiment started with
. If the concentrations are expressed in units of
%Activity, then one experiment started with
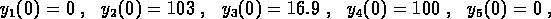
and the other with
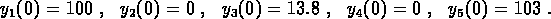
The data for the two experiments were combined and the two time series were fit simultaneously to determine
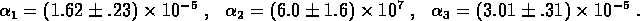
The fits accounted for 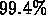 of the combined total variance in the two
measured records.
The measurements and the fits are shown in Figure 13 where thrombin concentration
of the combined total variance in the two
measured records.
The measurements and the fits are shown in Figure 13 where thrombin concentration 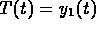 is plotted against t measured in hours.
is plotted against t measured in hours.