Bert W. Rust, ACMD
Holly E. Rushmeier, Scientific Computing Environments Division
Philip A. Sanders, Building and Fire Research Laboratory
Christine D. Piatko, Computer Systems Laboratory
As part of an effort to quantify the effectiveness of lighting in a working environment, this project seeks to compute the response of the human eye to a given two-dimensional luminance field like the test pattern given in Figure 10.
Figure 10: A luminance field test pattern
Figure 11: The estimated contrast sensitivity function
Figure 12: The perceived luminance field
The two-dimensional Fourier amplitude spectrum of the field is multiplied by the contrast sensitivity function of the eye to generate the internal representation which visual psychophysicists believe is the basis for the human percept.
The contrast sensitivity function is based on
measured data taken radially in the vertical (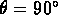
) and
oblique (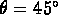
) directions. It is assumed that the
contrast sensitivity in the horizontal (
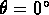) direction
is the same as that in the vertical direction, and that the whole function
is symmetric about the origin of the frequency space. This suggests a
contrast sensitivity function of the form
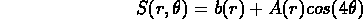
where r is the radial distance from the origin (measured in cycles per degree)
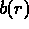and 
and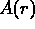 
are, respectively, a baseline and an amplitude function
which must be approximated from the measurements.
Discrete approximations of these functions are obtained by averaging and
differencing the vertical and oblique measurements. Functional representations
are then obtained by fitting optimal smoothing splines to these approximations,
with each point weighted inversely by its estimated standard deviation.
The smoothing constant in each case was chosen to minimize the
generalized cross-validation statistic. A representation of
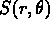is shown in Figure 11 where the horizontal and
vertical frequency scales range between -34 and +34 cycles/degree.
Multiplying the Fourier amplitude spectrum of the test pattern in Figure 10 by the contrast sensitivity function in Figure 11 and computing the inverse Fourier transform of the result gives the perceived field shown in Figure 12.