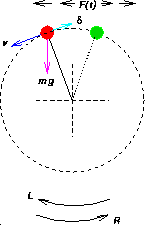
Figure 9: Motion of a pendulum subject to downward gravitational force, viscous damping
 proportional to angular
speed, and periodic external torque F.
proportional to angular
speed, and periodic external torque F.
Timothy J. Burns, ACMD
Christopher K.R.T. Jones, Brown University
Work continued on some problems involving resonance and chaos in multifrequency physical systems, which arise in many applications, including nonlinear conservative systems with periodic forcing, weakly coupled oscillators with small friction, fast rotation of heavy rigid bodies in a resisting medium, and electrical circuits with Josephson junctions, which are the basis of the present NIST voltage standard. This collaboration began during an internally funded NIST effort to develop competency in nonlinear dynamics and chaos. Prior work on this project has focused on analyzing the prototypical two-frequency problem of a damped mathematical pendulum with periodic external torque (see Figure 9). When the external torque is constant, the pendulum can exhibit two different stable oscillatory states: (i) gravity is balanced by torque, and the pendulum oscillates with slowly decreasing amplitude about an equilibrium position; (ii) energy added by the external torque is balanced by the energy dissipated, and there is a stable rotation of the pendulum, with constant average speed. For certain combinations of dissipation and periodic torque, the pendulum can behave unpredictably, slowing down as it swings close to the vertical position, and then either continuing to rotate in the same direction, or else reversing direction, etc. There have been a number of recent studies of chaotic motions of this type arising in models of dynamics in the Solar System. It was proved earlier as part of this project, that if the torque changes sign slowly enough, then the system can spend a long time in a stable rotary state, with its average rotation rate slowly decreasing in magnitude until the pendulum stops rotating and begins to oscillate with decreasing amplitude about the stable nonrotary state, where it remains permanently. This year, it was shown that the earlier results continue to hold in the case of much weaker damping and external forcing. Depending on the asymptotic scaling, both cases arise in models which have been proposed for the evolution of Mercury and the Moon into their present respective 3:2 and 1:1 spin-orbit resonant states under the influence of weak tidal dissipation. The theory provides a convincing explanation for how such resonances can evolve. Current efforts are focused on writing up this work for publication in a planetary physics journal.

Figure 9: Motion of a pendulum subject to downward
gravitational force, viscous damping  proportional to angular
speed, and periodic external torque F.
proportional to angular
speed, and periodic external torque F.