


Next: Stability of a
Up: Modeling of Physical
Previous: Parameter Identification
M. Lyell and G. B. McFadden ACMD
R. G. Rehm, CAML
R. F. Berg, Chemical Science and Technology Laboratory
The study of fluid systems near their thermodynamic critical point
is a very active research area in condensed matter physics. The critical
point is characterized by a unique temperature, pressure, and
density; roughly speaking, at temperatures below the critical temperature,
two-phase equilibria between the liquid and vapor phases
are possible, and above the critical temperature the distinction
between liquid and vapor is lost and only one phase occurs.
As the critical point is approached, thermophysical properties of
the fluid are observed to develop singularities, and this behavior
is also predicted theoretically. The Thermophysics Division
has a long-standing research program in this area,
and has performed many fundamental experimental studies of fluid
behavior near the critical point. Current plans include shuttle-based
experiments with xenon to measure the behavior of the fluid's
viscosity near the critical point.
A complication with terrestrial measurements of critical fluids
is the density stratification that occurs in the presence of a
gravitational field. Ideally, one would perform measurements on
a homogeneous isothermal system of constant density. However,
in this situation the compressibility of the fluid is very large, and
is predicted to diverge at the critical point;
as a result the fluid density stratifies under
its own weight. Stratification places a limit on how close to the critical point
measurements can be made before deviations from ideal conditions become
significant. For example, density stratification allows the fluid to undulate
in modes, called internal wave modes, which cannot be sustained in a
homogeneous fluid.
Therefore, measurements are being performed in
microgravity environments, where the effects of gravity are less
important.
In experimental work by Robert Berg (838)
to measure fluid viscosity near the critical point, a rectangular
paddle whose surface consists
of a fine-wire mesh that is permeable to the fluid is driven sinusoidally
in the fluid with a given frequency. The fluid viscosity can be inferred
by measuring the amplitude of the motion and the force necessary to sustain the
motion. It is observed in experiments under terrestrial conditions that
at certain driving frequencies the response is more complicated than
would be predicted by simple models of the fluid response to the paddle;
for the success of space-based experiments it is necessary to understand
whether or not these anomalies are related to the strength of the gravitational
field. In particular, Dr. Berg suggested that a resonance is taking place
between natural frequencies of internal waves in the system and
the driving frequency of the paddle.
Margaret Lyell, who is on sabbatical from the Mechanical
and Aerospace Engineering
Department of West Virginia University, has been collaborating with
G. McFadden and R. Rehm in CAML with the intention of identifying
the nature of the internal waves and the flow field associated with the
waves in both a qualitative and quantitative manner. The most
general set of equations which govern the continuum fluid behavior are
those of conservation of mass, conservation of momentum (Navier-Stokes),
and conservation of energy, along with an equation of state.
For the isothermal experiments, it
was determined that compressibility and viscous effects on the wave motion could be neglected, and a Boussinesq approximation is valid.
Expansion around the base state of zero motion leads to a set of
perturbation equations. Due to the density stratification,
the system in general could not be solved in closed form. The
density stratification itself changes depending upon the temperature of
the isothermal system. If the temperature of interest is "far" from
the critical temperature (and above it), a closed form approximate
solution can be obtained. The general approach required a
computational solution. A Galerkin collocation scheme involving a
Chebyshev expansion was utilized.
Results thus far include the determination of the eigenfrequencies
for various modes over a large range of selected temperature values
as illustrated in the accompanying figure.
Good agreement with the experimental frequency results has been
obtained, thus permitting identification and explanation of the
experimental observations. Also, visualization of the calculated flow field
has been accomplished by utilizing the closed form solution at a selected
temperature far above the critical temperature.
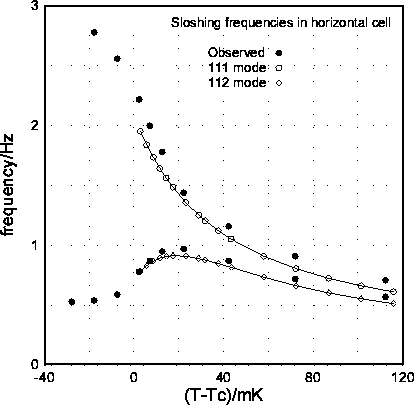
Figure 14: Comparisons of experimental data of R. Berg for the
measured resonant frequencies of the fluid viscometer as a
function of temperature T relative to the critical temperature 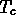 .
Data for two of the observed modes are shown (solid circles),
and theoretical predictions based on a model of internal-wave motion
are indicated by the two curves.
.
Data for two of the observed modes are shown (solid circles),
and theoretical predictions based on a model of internal-wave motion
are indicated by the two curves.



Next: Stability of a
Up: Modeling of Physical
Previous: Parameter Identification

 .
Data for two of the observed modes are shown (solid circles),
and theoretical predictions based on a model of internal-wave motion
are indicated by the two curves.
.
Data for two of the observed modes are shown (solid circles),
and theoretical predictions based on a model of internal-wave motion
are indicated by the two curves.