


Next: Deblurring of PET
Up: Image Deblurring
Previous: Probabilistic Nonlinear Image
Alfred S. Carasso, ACMD
The SECB method is a non-iterative linear method based on the novel `slow
evolution' constraint. Previous linear methods have sought to stabilize the
deblurring problem by imposing smoothness constraints on the solution. As
already noted, this is a dangerous procedure in medical imaging, as well as
other contexts, where singularities may be of vital interest. The `slow
evolution' constraint is highly effective in suppressing noise amplification
without imposing any smoothness on the unknown solution. This constraint
is imposed via a regularization parameter K obtained from a-priori
considerations. Knowledge of the statistical character of the data noise does
not enter the SECB formulation.
Because it is a direct method, SECB deblurring produces a sharp image in
one iteration. An obvious question concerns the quality of the
reconstructed image as compared with probabilistic nonlinear algorithms that
are designed to be optimal for specific noise processes such as Poisson or
Gaussian noise.
To answer this question, an exhaustive series of numerical experiments was
undertaken. A sharp MRI 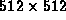 sagittal head image,
sagittal head image, 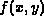 , was
artificially blurred by convolution with a known point spread function,
, was
artificially blurred by convolution with a known point spread function,
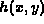 , to form a blurred image
, to form a blurred image 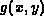 . Noise was then added to the blurred
image, and all of the above-mentioned deblurring procedures were applied to
this noisy blurred image. The selected MRI image
. Noise was then added to the blurred
image, and all of the above-mentioned deblurring procedures were applied to
this noisy blurred image. The selected MRI image 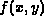 contains
highly-detailed structures, and is representative of a broad class of images of
interest in medical imaging. The blurring kernel
contains
highly-detailed structures, and is representative of a broad class of images of
interest in medical imaging. The blurring kernel 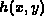 was chosen to
simulate X-ray scattering in radiology. In these experiments, knowledge of the
exact solution allows computation of the
was chosen to
simulate X-ray scattering in radiology. In these experiments, knowledge of the
exact solution allows computation of the 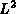 errors as the iteration
proceeds.
errors as the iteration
proceeds.
In the first set of experiments, the added noise was entirely due to
rounding-off the computed blurred image to integer values lying between 0 and
255. This relatively low level of noise (SNR = 22 db), permits restoration of
fine detail in the image. The point here is to test the reconstructive ability
of each algorithm. A characteristic feature of these iterative methods is the
fact that gross features in the image are fairly quickly reconstructed, while a
considerable number of iterations is typically necessary to reconstruct fine
detail. The SECB procedure reconstructs both low and high frequency information
simultaneously. This dichotomy is illustrated by the first four rows of the
accompanying table. In one experiment involving the Lucy-Richardson method,
5000 iterations were necessary to achieve the same quality of reconstruction
as in the SECB method. The differences in computing times are very dramatic in
this case. (All computations were done on an SGI R4000 workstation).
In the second set of experiments, the blurred image was severely degraded by
adding Poisson noise, resulting in SNR = 10 db. In this case, there is little
possibility of reconstructing fine detail, by any method. Indeed, the
Lucy-Richardson and Hunt iterations quickly deteriorated, as predicted,
producing unrecognizable images after 200 iterations. With 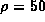 , the
Maximum Entropy method converged nicely in 1000 iterations, lasting 5.6 hours.
However, the resulting image had lower resolution than could be obtained with
the SECB method in 20 seconds. The Lucy-Richardson and Hunt iterations were
terminated at the point where the
, the
Maximum Entropy method converged nicely in 1000 iterations, lasting 5.6 hours.
However, the resulting image had lower resolution than could be obtained with
the SECB method in 20 seconds. The Lucy-Richardson and Hunt iterations were
terminated at the point where the 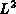 error was a minimum, (an option that is
not available in practice), at 87 and 68 iterations respectively. Even so, the
resulting images did not show any noticeable improvement over the SECB method.
This is significant since the nonlinear procedures are optimized for Poisson
noise, while the SECB method operates with any noise process. This second set
of experiments is summarized in the last four rows of Table
1.
error was a minimum, (an option that is
not available in practice), at 87 and 68 iterations respectively. Even so, the
resulting images did not show any noticeable improvement over the SECB method.
This is significant since the nonlinear procedures are optimized for Poisson
noise, while the SECB method operates with any noise process. This second set
of experiments is summarized in the last four rows of Table
1.
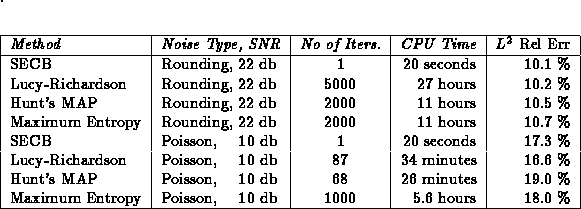
Table 1: Performance of SECB versus Nonlinear Procedures on  MRI Image
MRI Image
These experiments indicate that for a broad class of images, the above
nonlinear procedures do not offer any advantage. A well-designed linear method
such as SECB can produce results that are as good or better, at considerable
savings in computing time. Future work will examine different nonlinear
procedures, such as the `shock fitting' approach based on nonlinear partial
differential equations, and the Geman-McClure technique based on Gibbs prior
distributions in a Bayesian formulation.



Next: Deblurring of PET
Up: Image Deblurring
Previous: Probabilistic Nonlinear Image
Generated by [email protected] on Mon Aug 19 10:08:42 EDT 1996
 sagittal head image,
sagittal head image, 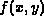 , was
artificially blurred by convolution with a known point spread function,
, was
artificially blurred by convolution with a known point spread function,
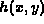 , to form a blurred image
, to form a blurred image 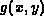 . Noise was then added to the blurred
image, and all of the above-mentioned deblurring procedures were applied to
this noisy blurred image. The selected MRI image
. Noise was then added to the blurred
image, and all of the above-mentioned deblurring procedures were applied to
this noisy blurred image. The selected MRI image 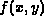 contains
highly-detailed structures, and is representative of a broad class of images of
interest in medical imaging. The blurring kernel
contains
highly-detailed structures, and is representative of a broad class of images of
interest in medical imaging. The blurring kernel 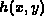 was chosen to
simulate X-ray scattering in radiology. In these experiments, knowledge of the
exact solution allows computation of the
was chosen to
simulate X-ray scattering in radiology. In these experiments, knowledge of the
exact solution allows computation of the 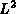 errors as the iteration
proceeds.
errors as the iteration
proceeds.
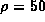 , the
Maximum Entropy method converged nicely in 1000 iterations, lasting 5.6 hours.
However, the resulting image had lower resolution than could be obtained with
the SECB method in 20 seconds. The Lucy-Richardson and Hunt iterations were
terminated at the point where the
, the
Maximum Entropy method converged nicely in 1000 iterations, lasting 5.6 hours.
However, the resulting image had lower resolution than could be obtained with
the SECB method in 20 seconds. The Lucy-Richardson and Hunt iterations were
terminated at the point where the 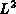 error was a minimum, (an option that is
not available in practice), at 87 and 68 iterations respectively. Even so, the
resulting images did not show any noticeable improvement over the SECB method.
This is significant since the nonlinear procedures are optimized for Poisson
noise, while the SECB method operates with any noise process. This second set
of experiments is summarized in the last four rows of Table
error was a minimum, (an option that is
not available in practice), at 87 and 68 iterations respectively. Even so, the
resulting images did not show any noticeable improvement over the SECB method.
This is significant since the nonlinear procedures are optimized for Poisson
noise, while the SECB method operates with any noise process. This second set
of experiments is summarized in the last four rows of Table

 MRI Image
MRI Image