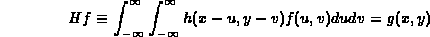
Nonlinear image deblurring procedures are widely believed to outperform conventional linear methods. Such nonlinear methods need iterative solutions that may require upwards of 20 hours of computing time on current desk-top workstations. Well-designed non-iterative methods that can produce results of comparable quality, a thousand times faster, would offer considerable advantages in medical diagnostic environments, in industrial process control systems, or in military and surveillance applications. Through its long-term research interest in ill-posed inverse problems, and its recent patented invention of the SECB deblurring method, ACMD has accumulated considerable expertise that enables it to undertake systematic evaluation of various image deblurring procedures.
The best-known nonlinear methods are based on probabilistic ideas centered on Bayes's theorem. Such a formulation offers the advantage of positivity and radiant flux conservation. In addition, optimal performance with respect to Poisson noise can often be designed into the algorithm. This is the case for the Lucy-Richardson method, the Maximum Likelihood method, the Expectation-Maximization algorithm, Hunt's Maximum A Posteriori method, and the Nunez-Llacer version of the Maximum Entropy method. These techniques are applied to the ill-posed linear imaging problem,
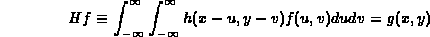
where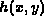 
is the known system point spread function,
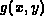is the blurred noisy image, and 
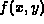is the desired deblurred
image. As one example, Hunt's MAP procedure is based on the iteration,
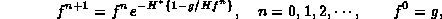
where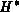 
is the adjoint of the
integral operator H.
Carasso has shown mathematically that except for the Maximum Entropy method,
all of the above iterative methods necessarily converge to the wrong
solution of Hf=g, in which severe noise amplification overwhelms the true
image. The Maximum Entropy method converges to a solution whose smoothness is
determined by an input parameter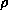 
. No successful theory exists for
choosing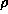 
in terms of a-priori information. Too small a value for 
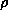leads to oversmooth solutions that may be dangerous in medical diagnostic
contexts. Thus, small lesions, tumors, microcalcifications, and other
singularities in the true image may be erased by the algorithm as it
maximizes the image entropy. Too large a value for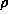 
brings out noise
which obscures important features in the image. A trial and error process for
choosing the optimal 
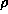must be used. This becomes very time consuming as
one must iterate to convergence, and evaluate the result, prior to selecting a
new value for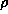 
.