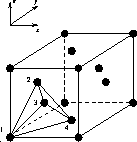
Figure 1: A schematic of an FCC lattice; atoms occupy the corners and the centers of the faces.
Richard J. Braun and Geoffrey B. McFadden, ACMD
Holly E. Rushmeier, Scientific Computing Environments Division
John W. Cahn, Materials Science and Engineering Laboratory
Adam A. Wheeler, University of Southampton
In solidification of the melt of either a pure material or an alloy, the solid form is often crystalline. The anisotropic nature of crystalline materials causes anisotropic interfacial properties as well; one such property is the melt-solid surface energy. The anisotropy of surface energy is intimately related to the formation of complex phase boundaries (microstructure) like dendrites observed in solidification. Diffuse-interface models of solidification have been very successful in computing complex solidification microstructure; however, the anisotropy of surface energy in these models is incorporated in an ad hoc way in the coefficients of the equations. It is then natural to ask whether the anisotropy may be derived as a consequence of the model.

Figure 1: A schematic of an FCC lattice; atoms occupy the corners and the
centers of the faces.
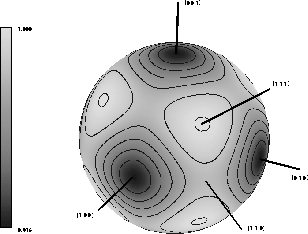
Figure 2: The variation of interfacial energy on the unit sphere for
interphase boundaries for one set of conditions. The [100] direction
is parallel to x, [010] is parallel to y, etc.
A diffuse-interface theory of ordering of a binary alloy on a face-centered-cubic (FCC) crystal lattice has been developed. A sketch of the basic cube of an FCC crystal in shown in Figure 1. A continuum, multiple-order-parameter theory is used that incorporates the underlying symmetries of the FCC crystal in both the bulk and gradient-energy terms of the free energy. With the theory, interphase and antiphase boundaries have been computed for general orientations with respect to the fixed crystal axes. They are able to compute the spatial structure of these interfaces, which compare very well with previous calculations by Kikuchi and Cahn using the (discrete) cluster variation method. The orientation dependence of the interfacial energy of the interphase boundaries has also been determined, and is shown to exhibit strong cubic symmetry. The relative anisotropy in the interfacial energy is shown in Figure 2. The anisotropy due to the lattice is a natural consequence of the multiple-order-parameter formulation, and so anisotropy is not incorporated in an ad hoc fashion as in a single-order-parameter theory. For the parameters studied, the anisotropy of the interfacial energy of the interphase boundaries is not sufficiently strong to cause edges or corners in equilibrium shapes. The kinetic anisotropy, on the other hand, is much stronger, and causes edges and corners to form in the growth shapes. Study of the energy for anti-phase boundaries as a function of temperature are currently underway; they are expected to be sufficiently anisotropic to cause edges and corners in the equilibrium shapes. These results may be extended to include concentration variation within and dynamics of the phase boundaries.