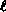 but different values of
total angular momentum j.
Thus, for example, if there were 2 electrons in a p shell, we assign
an electron population of
4/3 to the
but different values of
total angular momentum j.
Thus, for example, if there were 2 electrons in a p shell, we assign
an electron population of
4/3 to the 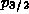 state and 2/3 to the
state and 2/3 to the 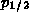 state.
state.
These calculations are all carried out in the framework of generalized Kohn-Sham theory ([5], and Chapter 7 of Ref. [3]). Details of the LDA, LSD, RLDA, and ScRLDA formalisms are described in independent sections below; here we focus on matters that are generic to all these approximations.
We utilize the central field
approximation, with conventional labelling of principal
and angular momentum quantum numbers of electronic orbitals.
We limit our calculations to the ground electronic configurations
of the first 92 neutral atoms and singly-charged cations of
the periodic table; the specific configurations used are described
below. In cases of partially filled electronic subshells,
fractional occupancies are assigned to orbitals with different azimuthal
quantum number, m, to accomplish a spherical averaging of the
charge distribution. In the
case of RLDA, this extends to averaging over subshells with
the same orbital angular momentum 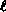 but different values of
total angular momentum j.
Thus, for example, if there were 2 electrons in a p shell, we assign
an electron population of
4/3 to the
but different values of
total angular momentum j.
Thus, for example, if there were 2 electrons in a p shell, we assign
an electron population of
4/3 to the 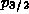 state and 2/3 to the
state and 2/3 to the 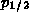 state.
state.
The results presented here derive from four codes, written independently. These were found to give results of good mutual consistency, provided that the numerical approximations within each code were varied until a very high degree of convergence was obtained within each code. The original authors of the four codes are, in alphabetical order
These codes were used by us with the permission of their authors. However, all codes required modification to obtain numerical convergence to the target accuracy of 1 microHartree in total energy. These modifications were not subject to review by the original authors. Some of these codes circulate relatively freely within the electronic structure community, so we must caution readers that a given available version of any one of these codes need not yield results identical to those presented here. Our purpose in this study was to use robust tested tools to accomplish a specific task, not to provide a relative ranking of various codes. For this reason, we do not give details of individual code performance beyond what is necessary to describe the uncertainties in the results, and we refer to each code by a numerical label between 1 and 4, chosen arbitrarily.