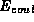 ,
the electron-nucleus energy,
,
the electron-nucleus energy,  , and the exchange-correlation
energy,
, and the exchange-correlation
energy, 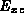 , which takes into account approximately the fact that
an electron does not interact with itself, and that electron
correlation effects occur.
, which takes into account approximately the fact that
an electron does not interact with itself, and that electron
correlation effects occur.
In the local-density approximation (LDA),
the many-electron problem is approximated by
a set of single-particle equations which are solved with the
self-consistent field method. The total energy is minimized.
The total energy is taken to be the sum of a kinetic energy, T,
the classical Hartree term for the electron density, 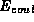 ,
the electron-nucleus energy,
,
the electron-nucleus energy,  , and the exchange-correlation
energy,
, and the exchange-correlation
energy, 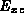 , which takes into account approximately the fact that
an electron does not interact with itself, and that electron
correlation effects occur.
, which takes into account approximately the fact that
an electron does not interact with itself, and that electron
correlation effects occur.
One solves the Kohn-Sham orbital equations
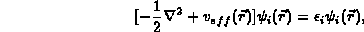
with
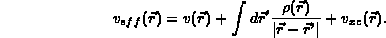
The charge density 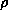 is given by
is given by

where the 2 accounts for double occupancy of each spatial orbital
because of spin degeneracy.
The potential, 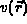 , is the external potential;
in the atomic case, this is
, is the external potential;
in the atomic case, this is 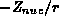 where Z is the atomic number.
The exchange correlation potential,
where Z is the atomic number.
The exchange correlation potential, 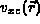 , is a function only of
the charge density, i.e.,
, is a function only of
the charge density, i.e., 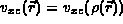 .
We use the functional of
Vosko, Wilk, and Nusair (1980)[4],
as described above.
.
We use the functional of
Vosko, Wilk, and Nusair (1980)[4],
as described above.
The various parts of the total energy are given by:
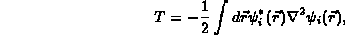
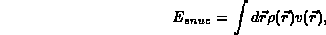
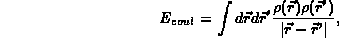
and
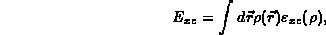
where 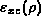 is the exchange-correlation energy per particle
for the uniform electron gas of density
is the exchange-correlation energy per particle
for the uniform electron gas of density 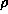 .
This approximation for
.
This approximation for 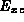 is the principal approximation of the LDA.
is the principal approximation of the LDA.