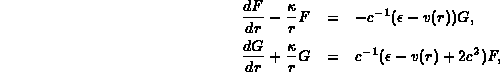
The relativistic local-density approximation[13] (RLDA) may be obtained from the (nonrelativistic) local-density approximation (LDA) by substituting the relativistic kinetic energy operator for its nonrelativistic counterpart, and using relativistic corrections to the local-density functional. We use the relativistic corrections proposed by MacDonald and Vosko [7].
Here, we give the radial equations which are solved by our programs:
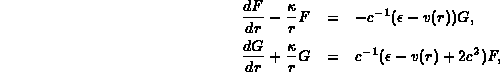
where  is the eigenvalue in Hartrees, and c is the speed
of light;
is the eigenvalue in Hartrees, and c is the speed
of light;  = 0 describes a free electron with
zero kinetic energy. The functions
= 0 describes a free electron with
zero kinetic energy. The functions 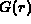 and
and 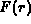 are related to the Dirac spinor by
are related to the Dirac spinor by
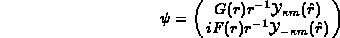
where  is a Pauli spinor[12].
is a Pauli spinor[12].
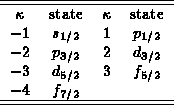
Dirac's  quantum number, along with the azimuthal quantum number
m, determines the angular dependence of the state. For the central-field
problem, the levels with various m are degenerate and hence not solved for
separately. The following table relates the values of
quantum number, along with the azimuthal quantum number
m, determines the angular dependence of the state. For the central-field
problem, the levels with various m are degenerate and hence not solved for
separately. The following table relates the values of  used in this
project to the more common spectroscopic notation.
used in this
project to the more common spectroscopic notation.
The charge density is obtained from
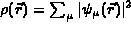 where
where 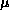 runs over the four components of the Dirac spinor.
runs over the four components of the Dirac spinor.