 .
.
Javier Bernal, ACMD
A triangulation for a finite set of points S in the plane is a finite collection of triangles in the plane having pair-wise disjoint interiors, each of which intersects S exactly at its vertices, and the union of which is the convex hull of S. Given a triangulation T for S, we say that T is Delaunay if for each triangle in T there does not exist a point of S inside the circumcircle of the triangle. A (Delaunay) tetrahedralization is similarly defined with tetrahedra and spheres taking the place of triangles and circles.
A more general triangulation can be defined.
Let S be as above, and let E be a finite collection,
possibly empty, of line segments with endpoints in S that
intersect only at points in S.
We say that a
triangulation T for S is constrained by E
if each line segment in E is the union of edges in T.
Given T, a triangulation for S
constrained by E, we say that T is
Delaunay constrained by E
if for each t in T there does not
exist a point P of S inside the circumcircle of t such
that no line segment in E intersects the interior of the convex
hull of 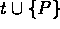 .
.
An algorithm has been developed for the insertion of a line segment into a constrained Delaunay triangulation by edge-swapping that produces a Delaunay constrained triangulation with the line segment as an additional constraint. A 3- dimensional version of the algorithm without the optimization steps for the Delaunay property has also been developed for attempting to insert a line segment into a tetrahedralization. It has been shown that for certain cases the failure of this algorithm to insert a line segment into a tetrahedralization is an indication that unless new vertices are added to the tetrahedralization the insertion is not possible. Finally, 3-dimensional problems have been identified that can be approached algorithmically as if they are 2-dimensional.
The ability to insert line segments is required when modeling surfaces that have breaks in their continuity or smoothness. 2- and 3-dimensional algorithms for the insertion of line segments are currently being developed and implemented. The 3-dimensional algorithm may require the addition of new vertices to the tetrahedralization.