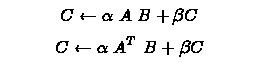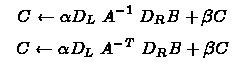The NIST Sparse BLAS (v. 0.9)

Sparse Matrix Computational Kernels

Karin Remington
Roldan Pozo
National Institute of Standards and Technology

---

See the working document of the BLAST Sparse Subcommittee for related information.
As part of the ongoing standardization effort in the BLAS Technical Forum, we are releasing the NIST Sparse BLAS Library for public review. We hope this motivates discussion with the larger user-community regarding interface, functionality, and performance issues.

---

Now available, Beta release of the NIST FORTRAN Sparse BLAS... details here

---

Performance measurements and testers are now available.
See performance studies.

Source code request service is now available.
See SourceService to dynamically generate specific routines from the library.

1. OVERVIEW
2. PERFORMANCE
3. DEVELOPER'S CORNER
4. DOCUMENTATION AND RELATED PAPERS
5. DISTRIBUTION
6. BUG REPORTS

The NIST Sparse BLAS (Basic Linear Algebra Subprogram) library provides computational kernels for fundamental sparse matrix operations:

• sparse matrix products,
  
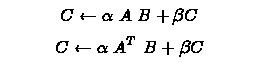
• solution of triangular systems,
  

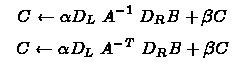
where A is sparse matrix, B and C are dense matrices/vectors, and D_L and D_R are diagonal matrices. This version of the NIST Sparse BLAS supports the following sparse formats: compressed-row, compressed-column, and coordinate storage formats, together with block and variable-block versions of these. Symmetric and skew-symmetric versions are also supported. See the User's Guide for documentation.

The routines are written in ANSI C and are callable from Fortran and C through the interface proposed in the Sparse BLAS Toolkit, see "A Revised Proposal for a Sparse BLAS Toolkit", by S. Carney, M. Heroux, G. Li, R. Pozo, K. Remington and K. Wu. Also see the companion paper, "A set of Level 3 Basic Linear Algebra Subprograms for sparse matrices", I. Duff, M. Marrone, G. Radiacti, C. Vittoli.

In addition to the Sparse BLAS Toolkit interface, developers have access to lightweight kernel routines. These Sparse BLAS Lite routines are unique to each parameter combination of the higher-level Toolkit interface. The Lite routines are designed for minimal overhead; they have no case statements, nor elaborate error-detection overhead. Thus, they are ideal for use on small matrices or to be used as efficient building blocks in higher-level routines. Some typical examples of the Lite routines:

		C <- A' * B             CSR_MatMult_CATB()
		C <- A * B + C          CSR_MatMult_CABC()
		C <- alpha*A*B + b*C    CSR_MatMult_CaBbC()
		C <- D*A^(-1)*B + C     CSR_MatTriangSlvLD_CDABC()

• NIST Sparse BLAS User's Guide (52 KB gzipped postscript file)
• "A Revised Proposal for a Sparse BLAS Toolkit", S. Carney, M. Heroux, G. Li, R. Pozo, K. Remington and K. Wu.
• "A set of Level 3 Basic Linear Algebra Subprograms for sparse matrices", I. Duff, M. Marrone, G. Radiacti, C. Vittoli, Rutherford Appleton Laboratory Technical Report, RAL-TR-95-049, 1995.

The complete installation (with testing) requires about 20 megabytes of free disk space. To request only specific routines from the library, see SourceService code request form.

• NIST Sparse BLAS: Basic Toolkit v.0.9b (complete source code, 593 KB compressed shar file)
• NIST Sparse BLAS: Basic Toolkit v.0.9b (complete source code, 238 KB zip file)
• SourceService code request form (individual routines generated upon request)
• Information on source code generation scheme

WARNING: MISSING FILE: The script ex_proto.pl was inadvertantly left out of the distribution which was available prior to 8/7/96. It is only required if the user regenerates the library source code (after optimizing the kernels, for example). It can be obtained here, ex_proto.pl, and should be placed in the include subdirectory with filename ex_proto.pl. This file is included in the distribution currently available.