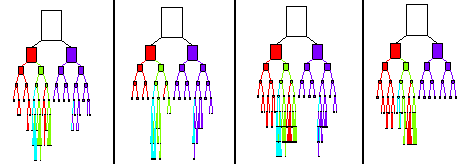
Adaptive refinement tree on each of the four processors.

An adaptive multigrid method solves an elliptic PDE by beginning with a very coarse grid and cycling through phases of adaptive refinement/derefinement of the grid and multigrid solution of the linear system of equations resulting from discretization of the PDE on the adaptive grid. In a parallel adaptive multigrid method, the adaptive refinement phase can cause the load balance over the processors to become unequal. If the load is too unbalanced, the grid must be repartitioned and redistributed before continuing with the solution phase. Alternatively, the load balancing step can occur before refinement, known as predictive load balancing.
An important part of a parallel adaptive multigrid method is the method for determining this partition. In this context, it must not only produce equal sized sets to balance the load and minimize cut edges to reduce communication, but must also be very fast to not dominate the computation time of a fast multigrid method, and must produce similar partitions on a grid and a refinement/derefinement of that grid to reduce redistribution costs.
The PHAML project developed a refinement-tree based partitioning method for partitioning grids that were created by adaptive refinement. The method applies not only to triangles, but also quadrilateral, and in 3D it applies to tetrahedra and hexahedra. The method was developed first as a recursive bisection method, and later as a k-way method to reduce the amount of communication overhead in a parallel implementation. It is also related to space filling curve methods.
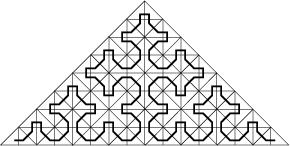
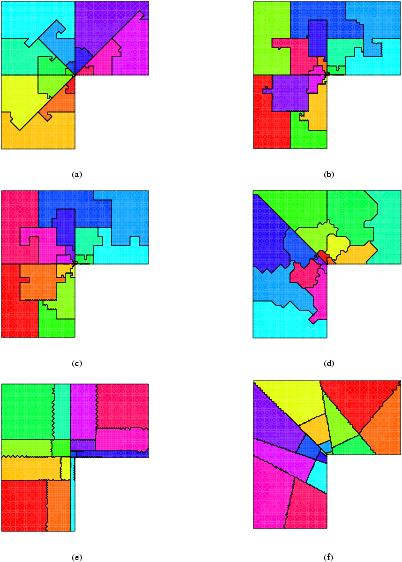
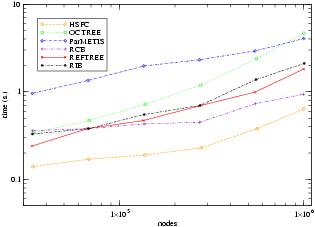
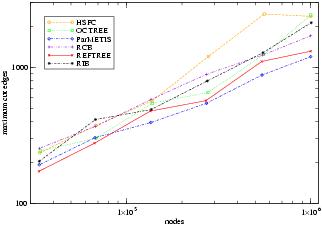
The method uses the refinement tree created by the adaptive refinement method. The leaves, which correspond to triangles in the grid, and interior nodes, which correspond to triangles that have been refined, may be weighted to reflect the work associated with each triangle. A weight of 1 at the leaves and 0 at the interior nodes will create partitions with equal numbers of triangles. The weights are summed to give a weight to every subtree. The tree is traversed in a truncated depth first manor as partitions are constructed. At each visited node, if the weight of that subtree will fit into the current partition, then all nodes in that subtree are assigned to the current partition. If they will not fit, then the children of the node are visited so the subtree is split among two or more partitions. When the current partition is filled, the next partition becomes current. By visiting the children in a carefully chosen order, a space filling curve is generated, and the partitions are guaranteed to be contiguous. In addition to the implementation in PHAML, the refinement-tree based partitioning method is implemented in Zoltan, a library of methods for dynamic load balancing. Using PHAML as an application code, a comparison of the partitioning methods in Zoltan was performed with an adaptively refined grid on an L-shaped domain. The methods are the refinement-tree based method (REFTREE), Hilbert space filling curve (HSFC), Octree (OCTREE), ParMETIS multilevel diffusion (ParMETIS), recursive coordinate bisection (RCB), and recursive inertial bisection (RIB). In this comparison, the refinement-tree based method shows a good balance between computation time and quality of partitions.
Publications
Mitchell, W.F., A Refinement-tree Based Partitioning Method for Dynamic Load Balancing with Adaptively Refined Grids , J. Par. Dist. Comp., 67 (4), 2007, pp. 417-429. ( pdf, 2.5M) ( link to journal )
Mitchell, W.F., Hamiltonian Paths Through Two- and Three-Dimensional Grids , NIST J. Res. , 110, (2005), pp. 127-136. ( gzipped postscript, 79k)
Mitchell, W.F., A Comparison of Three Fast Repartition Methods for Adaptive Grids, Proceedings of the Ninth SIAM Conference on Parallel Processing for Scientific Computing, 1999. ( gzipped postscript, 50k)
Mitchell, W.F., The Refinement-Tree Partition for Parallel Solution of Partial Differential Equations, NIST Journal of Research, 103 (1998), pp. 405-414. ( gzipped postscript, 96k)
Mitchell, W.F., Refinement Tree Based Partitioning for Adaptive Grids, Proceedings of the 7th SIAM Conference on Parallel Processing for Scientific Computing, SIAM, 1995, pp. 587-592. (gzipped postscript, 75k)
Last change to this page: April 3, 2007 Date this page created: March 28, 2007 Home Page