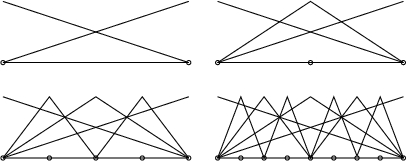
Construction of the linear h-hierarchical basis in 1D.

The multigrid method has been established as perhaps the most efficient method for solving the linear systems that arise from the discretization of differential equations. The popularity of this method can be attributed to the fact that it is optimal in the sense that one multigrid cycle can reduce the norm of the error by a factor that is bounded away from 1 independent of N, the size of the linear system, while using only O(N) operations.
The h-hierarchical basis multigrid method uses both the nodal basis and the h-hierarchical basis. It can be applied to grids that are uniform or adaptive in h, but must be uniform in p. The usual nodal basis for the space of piecewise linear functions on a given grid is defined by
In contrast, the h-hierarchical basis is defined using the family of nested grids from the refinement process. The h-hierarchical basis begins with the nodal basis on the initial grid. As refinement proceeds, with each element division one or more new nodes are added, and for each node a new basis function is defined as a nodal basis on the current grid, but the existing basis functions remain unchanged. A 2-level h-hierarchical basis for a grid can also be defined by starting with the nodal basis for the next-to-last refinement of the grid, and defining the higher level basis functions as above. It can be shown that conversion between the nodal basis and the 2-level h-hierarchical basis forms of coefficient vectors and finite element stiffness matrices is easily performed with a small number of operations per node.
The h-hierarchical basis multigrid algorithm is based on performing a sequence of transformations between nodal and 2-level h-hierarchical bases. In the 2-level stiffness matrix, the block corresponding to the coarse grid points is the nodal basis matrix of the coarse grid. The off-diagonal blocks provide a means of implicitly moving the residual between fine and coarse grids. Red-black Gauss-Seidel is used for the relaxation operator. It can be shown that with a uniform grid on a square domain and linear elements, this method is mathematically equivalent to a standard geometric multigrid method. It immediately extends the standard method to arbitrary domains, adaptive grids, and high order elements.
The h-hierarchical basis multigrid method cannot be used with nonuniform p, but it provides the motivation for the hp-hierarchical basis multigrid method for p-adaptive and hp-adaptive grids. In this method, the different values of p are considered to be the sequence of nested grids with the linear basis functions forming the "coarsest" grid. A V-cycle consists of performing a relaxation sweep with the entire matrix, followed by a relaxation sweep with the equations corresponding to the largest p omitted, and then with the two largest p omitted, etc. The "coarsest grid problem", i.e. the linear basis functions on the whole h grid, is solved by the h-hierarchical basis multigrid method. Relaxation sweeps are then performed while increasing the maximum value of p included until the entire matrix is used again. Numerical experiments with the method for Poisson's equation show that the rate of convergence is independent of both h and p.
| degrees of | max h | min p | max p | contraction |
|---|---|---|---|---|
| freedom | refinement | factor | ||
| 291 | 1 | 1 | 3 | .46 |
| 2320 | 7 | 1 | 5 | .42 |
| 18561 | 11 | 2 | 7 | .44 |
| 148480 | 15 | 3 | 10 | .44 |
| 1187894 | 19 | 3 | 12 | .40 |
| 4751622 | 22 | 3 | 14 | .41 |
Publications
Mitchell, W.F., The hp-Multigrid Method Applied to hp-Adaptive Refinement of Triangular Grids, Numerical Linear Algebra with Applications, 17, 2010, pp. 211-228. (preprint, pdf, 958K)
Mitchell, W.F., Optimal multilevel iterative methods for adaptive grids, SIAM J. Sci. Statist. Comput. 13 (1992), pp. 146-167.
Mitchell, W.F., Unified multilevel adaptive finite element methods for elliptic problems, Ph.D. thesis, Technical report UIUCDCS-R-88-1436, Department of Computer Science, University of Illinois, Urbana, IL, 1988. ( gzipped postscript, 194k)
Last change to this page: December 14, 2011 Date this page created: April 2, 2007 Home Page