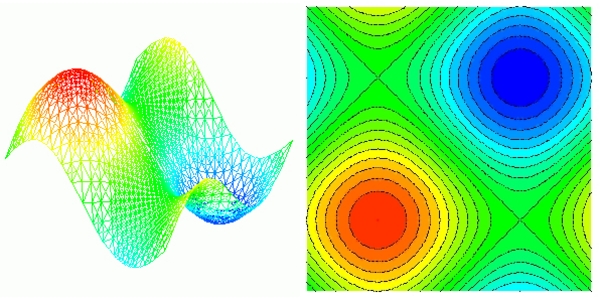
Two visualizations of a solution computed by the PHAML software.
PHAML primarily solves linear, scalar, elliptic, partial differential equation boundary value problems in 2D, of the form
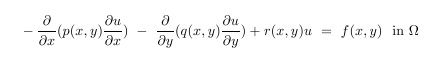
where the domain is a bounded, connected, region in the plane. It can have curved boundaries defined by parametric equations (x(s),y(s)), and can have holes. The boundary conditions can be Dirichlet on part of the boundary,
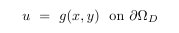
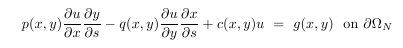
Note that when p=q, or the boundary is parallel to the x or y axis, the natural boundary conditions reduce to Neumann boundary conditions.
Periodic boundary conditions are also supported.
PHAML also solves elliptic eigenvalue problems of the form
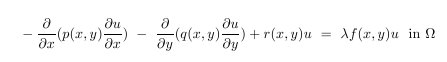
where &lambda is an unknown eigenvalue. Multiple eigenvalues can be computed simultaneously, and they do not need to be at the ends of the spectrum. For eigenvalue problems, the boundary conditions must be homogeneous, i.e. g(x,y)=0.
PHAML also supports multicomponent solutions, or systems of elliptic PDEs, or vector PDEs. In this case, the solution u has k components, i.e. is a vector of length k, and there are k equations. In the above notation, p, q, and r are kXk matrices and f and g are vectors of length k.
PHAML provides for the retention and evaluation of an "old" solution to help in the solution of other classes of problems that are not supported directly. For example, parabolic PDEs can be solved by a one step method by using the old solution to evaluate the solution at the previous time step. Also, nonlinear PDEs can be solved by using the old solution to evaluate the previous solution in a nonlinear iteration.
Publications
Mitchell, W.F., PHAML User's Guide , NISTIR 7374 , 2006. (original, pdf, 3.2M ) (latest revision, pdf)
Last change to this page: April 3, 2007 Date this page created: April 2, 2007 Contact: William Mitchell Home Page