The 2D Micromagnetic Interactive Solver: mmSolve2D

Overview
The application mmSolve2D is a micromagnetic computation engine capable of solving problems defined on two-dimensional square grids of three-dimensional spins. Within the OOMMF architecture, mmSolve2D is both a server and a client application. mmSolve2D is a client of problem description server applications, data table display and storage applications, and vector field display and storage applications. mmSolve2D is the server of a solver control service for which the only client is mmLaunch. It is through this service that mmLaunch provides a user interface window (shown above) on behalf of mmSolve2D.

Launching
mmSolve2D is started from the command line via

tclsh oommf.tcl mmSolve2D [standard options] [-restart <0|1>]

-restart <0|1>

Affects the behavior of the solver when a new problem is loaded. Default value is 0. When launched with -restart 1, the solver will look for basename.log and basename*.omf files to restart a previous run from the last saved state (where basename is the “Base Output Filename” specified in the input MIF 1.1 problem specification file). If these files cannot be found, then a warning is issued and the solver falls back to the default behavior (-restart 0) of starting the problem from scratch. The specified -restart setting holds for all problems fed to the solver, not just the first. (There is currently no interactive way to change the value of this switch.)

Once launched, an instance of mmSolve2D will appear next to a checkbutton on the Running Applications list in mmLaunch; selecting the checkbutton will open the mmSolve2D GUI interface. (mmSolve2D does not appear on the mmLaunch Programs launch list because it has been deprecated in favor of Oxsii. However, users may follow the edit instructions in the file oommf/app/mmlaunch/mmLaunchPrograms.tcl to reinstate mmSolve2D to the launch list.)

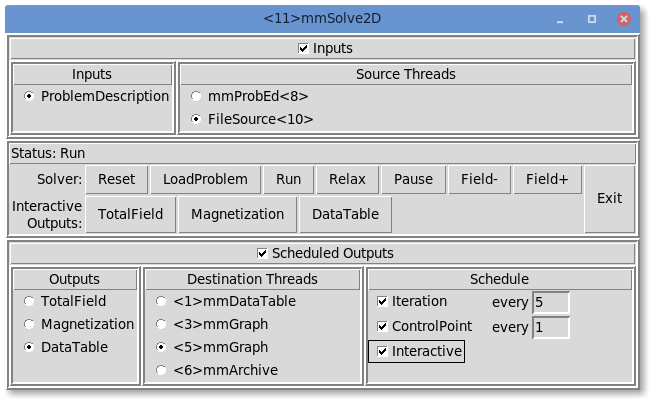
The GUI window is divided into panels, providing user interfaces to the Inputs, Outputs, and Controls of mmSolve2D.

Inputs
The top panel of the user interface window may be opened and closed by toggling the Inputs checkbutton. When open, the Inputs panel reveals two subpanels. The left subpanel contains a list of the inputs required by mmSolve2D. There is only one item in the list: ProblemDescription. When ProblemDescription is selected, the right subpanel (labeled Source Threads) displays a list of applications that can supply a problem description. The user selects from among the listed applications the one from which mmSolve2D should request a problem description.

Outputs
When mmSolve2D has outputs available to be controlled, a Scheduled Outputs checkbutton appears in the user interface window. Toggling the Scheduled Outputs checkbutton causes a bottom panel to open and close in the user interface window. When open, the Scheduled Outputs panel contains three subpanels. The Outputs subpanel is filled with a list of the types of output mmSolve2D can generate while solving the loaded problem. The three elements in this list are TotalField, for the output of a vector field representing the total effective field, Magnetization, for the output of a vector field representing the current magnetization state of the grid of spins, and DataTable, for the output of a table of data values describing other quantities of interest calculated by mmSolve2D.

Upon selecting one of the output types from the Outputs subpanel, a list of applications appears in the Destination Threads subpanel which provide a display and/or storage service for the type of output selected. The user may select from this list those applications to which the selected type of output should be sent.

For each application selected, a final interface is displayed in the Schedule subpanel. Through this interface the user may set the schedule according to which the selected type of data is sent to the selected application for display or storage. The schedule is described relative to events in mmSolve2D. An Iteration event occurs at every step in the solution of the ODE. A ControlPoint event occurs whenever the solver determines that a control point specification is met. (Control point specs are discussed in the Experiment parameters paragraph in the MIF 1.1 documentation, and are triggered by solver equilibrium, simulation time, and iteration count conditions.) An Interactive event occurs for a particular output type whenever the corresponding “Interactive Outputs” button is clicked in the Runtime Control panel. The Interactive schedule gives the user the ability to interactively force data to be delivered to selected display and storage applications. For the Iteration and ControlPoint events, the granularity of the output delivery schedule is under user control. For example, the user may elect to send vector field data describing the current magnetization state to an mmDisp instance for display every 25 iterations of the ODE, rather than every iteration.

The quantities included in DataTable output produced by mmSolve2D include:

• Iteration: The iteration count of the ODE solver.
• Field Updates: The number of times the ODE solver has calculated the effective field.
• Sim Time (ns): The elapsed simulated time.
• Time Step (ns): The interval of simulated time spanned by the last step taken in the ODE solver.
• Step Size: The magnitude of the last step taken by the ODE solver as a normalized value. (This is currently the time step in seconds, multiplied by the gyromagnetic ratio times the damping coefficient times $M_s$.)
• Bx, By, Bz (mT): The $x$, $y$, and $z$ components of the nominal applied field.
• B (mT): The magnitude of the nominal applied field (always non-negative).
• |m x h|: The maximum of the point-wise quantity $\vert\textbf{M}\times\textbf{H}_{eff}\vert/M_s^2$ over all the spins. This “torque” value is used to test convergence to an equilibrium state (and raise control point -torque events).
• Mx/Ms, My/Ms, Mz/Ms: The $x$, $y$, and $z$ components of the average magnetization of the magnetically active elements of the simulated part.
• Total Energy (J/m${}^3$): The total average energy density for the magnetically active elements of the simulated part.
• Exchange Energy (J/m${}^3$): The component of the average energy density for the magnetically active elements of the simulated part due to exchange interactions.
• Anisotropy Energy (J/m${}^3$): The component of the average energy density for the magnetically active elements of the simulated part due to crystalline and surface anisotropies.
• Demag Energy (J/m${}^3$): The component of the average energy density for the magnetically active elements of the simulated part due to self-demagnetizing fields.
• Zeeman Energy (J/m${}^3$): The component of average energy density for the magnetically active elements of the simulated part due to interaction with the applied field.
• Max Angle: The maximum angle (in degrees) between the magnetization orientation of any pair of neighboring spins in the grid. (The neighborhood of a spin is the same as that defined by the exchange energy calculation.)

In addition, the solver automatically keeps a log file that records the input problem specification and miscellaneous runtime information. The name of this log file is basename.log, where basename is the “Base Output Filename” specified in the input problem specification. If this file already exists, then new entries are appended to the end of the file.

Controls
The middle section of the user interface window contains a series of buttons providing user control over the solver. After a problem description server application has been selected, the LoadProblem button triggers a fetch of a problem description from the selected server. The LoadProblem button may be selected at any time to (re-)load a problem description from the currently selected server. After loading a new problem the solver goes automatically into a paused state. (If no problem description server is selected when the LoadProblem button is invoked, nothing will happen.) The Reset button operates similarly, except that the current problem specifications are used.

Once a problem is loaded, the solver can be put into any of three states: run, relax and pause. Selecting Relax puts the solver into the “relax” state, where it runs until a control point is reached, after which the solver pauses. If the Relax button is reselected after reaching a control point, then the solver will simply re-pause immediately. The Field+ or Field– button must be invoked to change the applied field state. (Field state schedules are discussed below.) The Run selection differs in that when a control point is reached, the solver automatically steps the nominal applied field to the next value, and continues. In “run” mode the solver will continue to process until there are no more applied field states in the problem description. At any time the Pause button may be selected to pause the solver. The solver will stay in this state until the user reselects either Run or Relax. The current state of the solver is indicated in the Status line in the center panel of the user interface window.

The problem description (MIF 1.x format) specifies a fixed applied field schedule. This schedule defines an ordered list of applied fields, which the solver in “run” mode steps through in sequence. The Field– and Field+ buttons allow the user to interactively adjust the applied field sequence. Each click on the Field+ button advances forward one step through the specified schedule, while Field– reverses that process. In general, the step direction is not related to the magnitude of the applied field. Also note that hitting these buttons does not generate a “ControlPoint” event. In particular, if you are manually accelerating the progress of the solver through a hysteresis loop, and want to send non-ControlPoint data to a display or archive widget before advancing the field, then you must use the appropriate “Interactive Output” button.

The second row of buttons in the interaction control panel, TotalField, Magnetization and DataTable, allow the user to view the current state of the solver at any time. These buttons cause the solver to send out data of the corresponding type to all applications for which the “Interactive” schedule button for that data type has been selected, as discussed in the Outputs section above.

At the far right of the solver controls is the Exit button, which terminates mmSolve2D. Simply closing the user interface window does not terminate mmSolve2D, but only closes the user interface window. To kill the solver the Exit button must be pressed.

Details
Given a problem description, mmSolve2D integrates the Landau-Lifshitz equation [12,17]

$$\frac{d\textbf{M}}{dt} = -\vert\bar{\gamma}\vert\,\textbf{M}\time... ...lpha}{M_s}\, \textbf{M}\times\left(\textbf{M}\times\textbf{H}_{\rm eff}\right),$$ (10.1)

where

$\textbf{M}$ is the pointwise magnetization (A/m),
$\textbf{H}_{\mbox{eff}}$ is the pointwise effective field (A/m),
$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\bar{\gamma}\\ \rule{1pt}{0pt}\end{array}$}$ is the Landau-Lifshitz gyromagnetic ratio (m/(A·s)),
$\alpha$ is the damping coefficient (dimensionless).

(See also the discussion of the Landau-Lifshitz-Gilbert equations in the Oxs documentation.)

The effective field is defined as

$$\textbf{H}_{\rm eff} = -\mu_0^{-1} \frac{\partial E}{\partial\textbf{M}}.$$

The average energy density $E$ is a function of $\textbf{M}$ specified by Brown's equations [5], including anisotropy, exchange, self-magnetostatic (demagnetization) and applied field (Zeeman) terms.

The micromagnetic problem is impressed upon a regular 2D grid of squares, with 3D magnetization spins positioned at the centers of the cells. Note that the constraint that the grid be composed of square elements takes priority over the requested size of the grid. The actual size of the grid used in the computation will be the nearest integral multiple of the grid's cell size to the requested size. It is important when comparing the results from grids with different cell sizes to account for the possible change in size of the overall grid.

The anisotropy and applied field energy terms are calculated assuming constant magnetization in each cell. The exchange energy is calculated using the eight-neighbor bilinear interpolation described in [6], with Neumann boundary conditions. The more common four-neighbor scheme is available as a compile-time option. Details can be found in the source-code file oommf/app/mmsolve/magelt.cc.

The self-magnetostatic field is calculated as the convolution of the magnetization against a kernel that describes the cell to cell magnetostatic interaction. The convolution is evaluated using fast Fourier transform (FFT) techniques. Several kernels are supported; these are selected as part of the problem description in MIF 1.x format. Each kernel represents a different interpretation of the discrete magnetization. The recommended model is ConstMag, which assumes the magnetization is constant in each cell, and computes the average demagnetization field through the cell using formulae from [23] and [2].

The Landau-Lifshitz ODE (10.1) is integrated using a second order predictor-corrector technique of the Adams type. The right side of (10.1) at the current and previous step is extrapolated forward in a linear fashion, and is integrated across the new time interval to obtain a quadratic prediction for $\textbf{M}$ at the next time step. At each stage the spins are renormalized to $M_s$ before evaluating the energy and effective fields. The right side of (10.1) is evaluated at the predicted $\textbf{M}$, which is then combined with the value at the current step to produce a linear interpolation of $d\textbf{M}/dt$ across the new interval. This is then integrated to obtain the final estimate of $\textbf{M}$ at the new step. The local (one step) error of this procedure should be $O(dt^3)$.

The step is accepted if the total energy of the system decreases, and the maximum error between the predicted and final $\textbf{M}$ is smaller than a nominal value. If the step is rejected, then the step size is reduced and the integration procedure is repeated. If the step is accepted, then the error between the predicted and final $\textbf{M}$ is used to adjust the size of the next step. No fixed ratio between the previous and current time step is assumed.

A fourth order Runge-Kutta solver is used to prime the predictor-corrector solver, and is used as a backup in case the predictor-corrector fails to find a valid step. The Runge-Kutta solver is not selectable as the primary solver at runtime, but may be so selected at compile time by defining the RUNGE_KUTTA_ODE macro. See the file oommf/app/mmsolve/grid.cc for all details of the integration procedure.

For a given applied field, the integration continues until a control point is reached. A control point event may be raised by the ODE iteration count, elapsed simulation time, or by the maximum value of $\vert\textbf{M}\times\textbf{H}_{\mbox{eff}}\vert/M_s^2$ dropping below a specified control point -torque value (implying an equilibrium state has been reached).

Depending on the problem size, mmSolve2D can require a good deal of working memory. The exact amount depends on a number of factors, but a reasonable estimate is 5 MB + 1500 bytes per cell. For example, a 1 µm $\times$ 1 µm part discretized with 5 nm cells will require approximately 62 MB.

Known Bugs
mmSolve2D requires the damping coefficient to be non-zero. See the MIF 1.1 documentation for details on specifying the damping coefficient.

When multiple copies of mmLaunch are used, each can have its own interface to a running copy of mmSolve2D. When the interface presented by one copy of mmLaunch is used to set the output schedule in mmSolve2D, those settings are not reflected in the interfaces presented by other copies of mmLaunch. For example, although the first interface sets a schedule that DataTable data is to be sent to an instance of mmGraph every third Iteration, there is no indication of that schedule presented to the user in the second interface window. It is unusual to have more than one copy of mmLaunch running simultaneously. However, this bug also appears when one copy of mmLaunch is used to load a problem and start a solver, and later a second copy of mmLaunch is used to monitor the status of that running solver.

OOMMF Documentation Team
September 27, 2024