Scalar field objects are documented first. Vector field objects are
considered farther below.
- Oxs_UniformScalarField:
- Returns the same constant value regardless of the import position.
The Specify block takes one parameter, value, which is the
returned constant value. This class is frequently embedded inline to
specify homogeneous material parameters. For example, inside a driver
Specify block we may have
Specify Oxs_TimeDriver {
...
Ms { Oxs_UniformScalarField {
value 8e5
}}
...
}
As discussed in
the section on Oxs_Ext
referencing in the MIF
2 documentation,
when embedding Oxs_UniformScalarField
or Oxs_UniformVectorField
objects, a notational shorthand is allowed that lists only the value.
The previous example is exactly equivalent to
Specify Oxs_TimeDriver {
...
Ms 8e5
...
}
where an implicit Oxs_UniformScalarField object is
created with value set to 8e5.
Examples: sample.mif, cgtest.mif.
- Oxs_AtlasScalarField:
- Declares values that are defined across individual regions of an
Oxs_Atlas. The Specify block looks like
-
Specify Oxs_AtlasScalarField {
- atlas atlas_spec
- multiplier mult
- default_value scalar_field_spec
- values {
- region1_label scalar_field_spec1
- region2_label scalar_field_spec2
- ...
}
- }
The specified atlas is used to map cell locations to
regions; the value at the cell location of the scalar field from the
corresponding values sub-block is assigned to that cell.
The default_value entry is optional; if specified, and if
a cell's region is not included in the values sub-block, then
the default_value scalar field is used. If default_value
is not specified, then missing regions will raise an error.
The scalar field entries may specify any of the scalar field types
described in this (Field Objects) section. As usual, one may provide
a single numeric value in any of the scalar_field_spec
positions; this will be interpreted as requesting a uniform (spatially
homogeneous) field with the indicated value.
If the optional multiplier value is provided, then each
field value is scaled (multiplied) by the value mult.
The vector field analogue to this class is
Oxs_AtlasVectorField,
which is described below in the vector fields portion of this
section.
Examples: diskarray.mif, ellipsoid.mif,
grill.mif, spinvalve.mif, tclshapes.mif.
- Oxs_LinearScalarField:
- Returns a value that varies linearly with position. The Specify
block has the form:
-
Specify Oxs_LinearScalarField {
- norm value
- vector {
vx
vy
vz }
- offset off
- }
If optional value norm is specified, then the given
vector is first scaled to the requested size. The
offset entry is optional, with default value 0. For any
given point (x, y, z), the scalar value returned by this
object will be
xvx + yvy + zvz + off.
Example:
spinvalve-af.mif.
- Oxs_RandomScalarField:
- Defines a scalar field that varies spatially in a random fashion.
The Specify block has the form:
-
Specify Oxs_RandomScalarField {
- range_min minvalue
- range_max maxvalue
- cache_grid mesh_spec
- }
The value at each position is drawn uniformly from the range declared by
the two required parameters, range_min and
range_max. There is also an optional parameter,
cache_grid, which takes a mesh specification that describes
the grid used for spatial discretization. If
cache_grid is not specified, then each call to
Oxs_RandomScalarField generates a different field. If you want to
use the same random scalar field in two places (as a base for setting,
say anisotropy coefficients and saturation magnetization), then specify
cache_grid with the appropriate (usually the base problem)
mesh.
Examples: randomshape.mif, stdprob1.mif.
- Oxs_ScriptScalarField:
- Analogous to the parallel
Oxs_ScriptVectorField
class, this class produces a scalar field dependent on a Tcl script
and optionally other scalar and vector fields. The Specify block has
the form
-
Specify Oxs_ScriptScalarField:name {
- script Tcl_script
- script_args { args_request }
- scalar_fields { scalar_field_spec ...}
- vector_fields { vector_field_spec ...}
- atlas atlas_spec
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- }
For each point of interest, the specified script is
called with the arguments requested by script_args
appended to the command, as explained in the User
Defined Support Procedures section of the MIF 2 file
format documentation. The value for script_args should be a
subset of {rawpt relpt minpt maxpt span scalars vectors}.
If rawpt is requested, then when the Tcl proc is called, at
the corresponding spot in the argument list the x, y,
z values of point will be placed, in problem coordinates (in
meters). The points so passed will usually be node points in the
simulation discretization (the mesh), but
this does not have to be the case in general. The relpt,
minpt, maxpt, and span rely on a definition of a
bounding box, which is an axes parallel parallelepiped. The
bounding box must be specified by either referencing an
atlas, or by explicitly stating the range via the three
entries xrange, yrange, zrange (in
meters). The minpt and maxpt arguments list the minimum
and maximum values of the bounding box (coordinate by coordinate),
while span provides the 3-vector resulting from
(maxpt - minpt). The relpt selection provides x_rel,
y_rel, z_rel, where each element lies in the range
[0, 1], indicating a relative position between minpt and
maxpt, coordinate-wise.
Each of the script_args discussed so far places exactly 3
arguments onto the Tcl proc argument list. The last two,
scalars and vectors, place arguments depending on the size
of the scalar_fields and vector_fields lists.
The scalar_fields value is a list of other scalar field
objects. Each scalar field is evaluated at the point in question,
and the resulting scalar value is placed on the Tcl proc argument
list, in order. The vector_fields option works similarly,
except each vector field generates three points for the Tcl proc
argument list, since the output from vector field objects is a three
vector. Although the use of these entries appears complicated, this
is a quite powerful facility that allows nearly unlimited control for
the modification and combination of other field objects. Both
scalar_fields and vector_fields entries are optional.
If script_args is not specified, the default value relpt
is used.
Note that if script_args includes relpt, minpt,
maxpt, or span, then a bounding box must be specified, as
discussed above. The following example uses the explicit range
method. See the Oxs_ScriptVectorField
documentation
for an example using an atlas specification.
proc Ellipsoid { xrel yrel zrel } {
set xrad [expr {$xrel - 0.5}]
set yrad [expr {$yrel - 0.5}]
set zrad [expr {$zrel - 0.5}]
set test [expr {$xrad*$xrad+$yrad*$yrad+$zrad*$zrad}]
if {$test>0.25} {return 0}
return 8.6e5
}
Specify Oxs_ScriptScalarField {
script Ellipsoid
xrange { 0 1e-6 }
yrange { 0 250e-9 }
zrange { 0 50e-9 }
}
This Oxs_ScriptScalarField object returns 8.6e5 if the import (x,y,z) lies within the ellipsoid
inscribed inside the axes parallel parallelepiped defined by (xmin=0,
ymin=0, zmin=0) and (xmax=1e-6, ymax=250e-9, zmax=50e-9), and 0
otherwise.
See also the discussion of the
ReadFile MIF extension command
for an example using
an imported image file for similar purposes.
Below is one more example, illustrating the use of the
vector_fields option.
proc DotProduct { x1 y1 z1 x2 y2 z2 } {
return [expr {$x1*$x2+$y1*$y2+$z1*$z2}]
}
Specify Oxs_FileVectorField:file1 {
atlas :atlas
file file1.omf
}
Specify Oxs_UniformVectorField:dir111 {
norm 1
vector {1 1 1}
}
Specify Oxs_ScriptScalarField:project {
script DotProduct
script_args vectors
vector_fields {:file1 :dir111}
}
The scalar field :project yields at each point in space the
projection of the vector field :file1 onto the [1,1,1] direction.
Examples: antidots-filled.mif, ellipsoid-fieldproc.mif,
manyregions-scriptfields.mif, manyspheres.mif,
varalpha.mif.
- Oxs_VecMagScalarField:
- The Oxs_VecMagScalarField class produces a scalar field
from a vector field by taking the norm of the vector field on a
point-by-point basis, i.e.,
|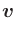 | =
| = 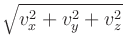 .
.
The Specify block has the form:
-
Specify Oxs_VecMagScalarField {
- field vector_field_spec
- multiplier mult
- offset off
- }
The multiplier and offset entries are applied
after the vector norm, i.e., the resulting scalar field is
mult * |v| + off. The default values
for mult and off are 1 and 0, respectively.
The functionality of the Oxs_VecMagScalarField class may be achieved
with the Oxs_ScriptScalarField class by using the
vector_fields option and a Tcl script to compute the vector
norm. However, this particular functionality is needed frequently
enough that a specialized class is useful. For example, this class can
be used in conjunction with a vector field object to set
both the saturation magnetization distribution (Ms) and the initial
magnetization:
Specify Oxs_FileVectorField:file1 {
atlas :atlas
file file1.omf
}
Specify Oxs_TimeDriver {
basename test
evolver :evolve
stopping_dm_dt 0.01
mesh :mesh
m0 :file1
Ms { Oxs_VecMagScalarField {
field :file1
}}
}
Example:
sample-vecrotate.mif.
- Oxs_ScriptOrientScalarField:
- Scalar fields provide scalar values as a function of position across
three-space. The Oxs_ScriptOrientScalarField class is used to
compose a transformation on the input position before evaluation by
a scalar field. The Specify block has the form:
-
Specify Oxs_ScriptOrientScalarField:name {
- field scalar_field_spec
- script Tcl_script
- script_args { args_request }
- atlas atlas_spec
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- }
The field argument should refer to a scalar field object.
The script is a Tcl script that should return a position
vector that will be sent on the field object to ultimately
produce a scalar value. The arguments to the Tcl_script are
determined by script_args, which should be a subset of
{relpt rawpt minpt maxpt span}. If any arguments other than
rawpt are requested, then the bounding box must be specified by
either the atlas option, or else through the three xrange,
yrange, zrange entries. The default value for
script_args is relpt.
The Oxs_ScriptOrientScalarField class can be used to change the
``orientation'' of a scalar field, as in the following simple example,
which reflects the :file1mag scalar field across the yz-plane:
Specify Oxs_FileVectorField:file1 {
atlas :atlas
file file1.omf
}
Specify Oxs_VecMagScalarField:file1mag {
field :file1
}
proc Reflect { x y z xmin ymin zmin xmax ymax zmax} {
return [list [expr {($xmax+$xmin-$x)}] $y $z]
}
Specify Oxs_ScriptOrientScalarField:reflect {
field :file1mag
script Reflect
script_args {rawpt minpt maxpt}
atlas :atlas
}
See also the
Oxs_ScriptOrientVectorField
class for
analogous operations on vector fields.
Example:
sample-reflect.mif.
- Oxs_AffineOrientScalarField:
- The Oxs_AffineOrientScalarField class is similar to the
Oxs_ScriptOrientScalarField class, except that the transformation
on the import position is by an affine transformation defined in terms
of a 3x3 matrix and an offset instead of a
Tcl script. Although this functionality can be obtained by an
appropriate Tcl script, the Oxs_AffineOrientScalarField is
easier to use and will run faster, as the underlying transformation is
performed by compiled C++ instead of Tcl script.
The Specify block has the form:
-
Specify Oxs_AffineOrientScalarField {
- field scalar_field_spec
- M
{ matrix_entries ... }
- offset {
offx
offy
offz }
- inverse invert_flag
- inverse_slack slack
- }
If
F(x) represents the scalar field specified by the
field value, then the resulting transformed scalar field is
F(Mx + off). Here M is a
3x3 matrix, which may be specified by a list
of 1, 3, 6 or 9 entries. If the matrix_entries list consists of a
single value, then M is taken to be that value times the identity
matrix, i.e., M is a homogeneous scaling transformation. If
matrix_entries consists of 3 values, then M is taken to be the
diagonal matrix with those three values along the diagonal.
If matrix_entries is 6 elements long, then M is assumed to be a
symmetric matrix, where the 6 elements specified correspond to M11,
M12, M13, M22, M23, and M33. Finally, if
matrix_entries is 9 elements long, then the elements specify the
entire matrix, in the order M11, M12, M13, M21,
..., M33. If M is not specified, then it is taken to be
the identity matrix.
The offset entry is simply a 3-vector that is added to
Mx. If offset is not specified, then
it is set to the zero vector.
It is frequently the case that the transformation that one wants to
apply is not
Mx + off, but rather the
inverse, i.e.,
M-1(x - off). Provided M
is nonsingular, this can be accomplished by setting the
inverse option to 1. In this case the matrix M.M-1 is
compared to the identity matrix, to check the accuracy of the matrix
inversion. If any entry in M.M-1 differs from I by more than the
8-byte float machine precision (typically
2e-16) times the value of
inverse_slack, then an error is raised. The default setting
for invert_flag is 0, meaning don't invert,
and the default setting for slack is 128.
Here is an example using Oxs_AffineOrientScalarField to rotate a
field by 90 degrees counterclockwise about the
z-axis. Note that the specified atlas is square in x and y, with
the origin of the atlas coordinates in the center of the atlas volume.
Specify Oxs_BoxAtlas:atlas {
xrange {-250e-9 250e-9}
yrange {-250e-9 250e-9}
zrange { -15e-9 15e-9}
}
Specify Oxs_FileVectorField:file1 {
atlas :atlas
file file1.omf
}
Specify Oxs_VecMagScalarField:file1mag {
field :file1
}
Specify Oxs_AffineOrientScalarField:reflect {
field :file1mag
M { 0 1 0
-1 0 0
0 0 1 }
}
See also the
Oxs_AffineOrientVectorField
class for
analogous operations on vector fields.
Example:
sample-rotate.mif.
- Oxs_AffineTransformScalarField:
- Like the Oxs_AffineOrientScalarField class, this class composes
an affine transform with a separate scalar field, but in this case the
affine transform is applied after the field evaluation.
The Specify block has the form:
-
Specify Oxs_AffineTransformScalarField {
- field scalar_field_spec
- multiplier mult
- offset off
- inverse invert_flag
- }
If
F(x) represents the scalar field specified by the
field value, then the resulting scalar field is
mult*F(x) + off. Since the output
from F is a scalar, both multiplier and offset
are scalars. If inverse is 1, then the transform is changed
to
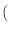 F(x) - off
F(x) - off /mult,
provided mult is non-zero.
/mult,
provided mult is non-zero.
The default values for mult, off, and
invert_flag are 1, 0, and 0, respectively. The field
value is the only required entry.
The functionality provided by Oxs_AffineTransformScalarField can
also be produced by the
Oxs_ScriptScalarField
class with the
scalar_fields entry, but the Oxs_AffineTransformScalarField
class is faster and has a simpler interface. See also the
Oxs_AffineTransformVectorField
class for analogous
operations on vector fields.
Example:
sample-rotate.mif.
- Oxs_ImageScalarField:
- This class creates a scalar field using an image. The Specify block has
the form
-
Specify Oxs_ImageScalarField:name {
- image pic
- invert invert_flag
- multiplier mult
- offset off
- viewplane view
- atlas atlas_spec
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- exterior ext_flag
- }
The image is interpreted as a monochromatic map, yielding a
scalar field with black corresponding to zero and white to one if
invert is 0 (the default), or with black corresponding to 1
and white to 0 if invert is 1. Color images are converted to
grayscale by simply summing the red, green, and blue components. A
multiplier option is available to change the range of values
from [0, 1] to
[0,mult], after which the
offset value, if any, is added.
The viewplane is treated in the same manner as the
Oxs_ImageAtlas viewplane option, and should
likewise take one of the three two-letter codes xy (default),
zx or yz. The spatial scale is adjusted to fit the volume
specified by either the atlas or
xrange/yrange/zrange selections. If the specified volume
does not fill the entire simulation volume, then points outside the
specified volume are handled as determined by the exterior
setting, which should be either a floating point value, or one of the
keywords boundary or error. In the first case, the floating
point value is treated as a default value for points outside the image,
and should have a value in the range [0, 1]. The multiplier and offset
adjustments are made to this value in the same way as to points inside
the image. If ext_flag is boundary, then points outside the
image are filled with the value of the closest point on the boundary of
the image. If ext is error (the default), then an error
is raised if a value is needed for any point outside the image.
Examples: rotatecenterstage.mif, sample-reflect.mif.
- Oxs_UniformVectorField:
- Returns the same constant value regardless of the import position.
The Specify block takes one required parameter, vector,
which is a 3-element list of the vector to return, and one optional
parameter, norm, which if specified adjusts the size of
export vector to the specified magnitude. For example,
-
Specify Oxs_UniformVectorField {
- norm 1
- vector {1 1 1}
- }
This object returns the unit vector (a, a, a), where
a=1/sqrt(3), regardless of the import
position.
This class is frequently embedded inline to specify spatially uniform
quantities. For example, inside a driver Specify block we may have
Specify Oxs_TimeDriver {
...
m0 { Oxs_UniformVectorField {
vector {1 0 0}
}}
...
}
As discussed in
the section on Oxs_Ext
referencing in the MIF
2 documentation,
when embedding Oxs_UniformVectorField
or Oxs_UniformScalarField
objects, a notational shorthand is allowed that lists only the required
value. The previous example is exactly equivalent to
Specify Oxs_TimeDriver {
...
m0 {1 0 0}
...
}
where an implicit Oxs_UniformVectorField object is
created with the value of vector set to {1 0 0}.
Examples: sample.mif, cgtest.mif.
- Oxs_AtlasVectorField:
- Declares vector values that are defined across individual regions of
an Oxs_Atlas. The Specify block has the form
-
Specify Oxs_AtlasVectorField {
- atlas atlas_spec
- norm magval
- multiplier mult
- default_value vector_field_spec
- values {
- region1_label vector_field_spec1
- region2_label vector_field_spec2
- ...
}
- }
Interpretation is analogous to the
Oxs_AtlasScalarField
specify block, except here the output values are 3 dimensional
vectors rather than scalars. Thus the values associated with each
region are vector fields rather than scalar fields. Any of the
vector field types described in this (Field Objects) section may be
used. As usual, one may provided a braced list of three numeric
values to request a uniform (spatially homogeneous) vector field with
the indicated value.
The optional norm parameter causes each vector value to be
scaled to have magnitude magval. The optional
multiplier value scales the field values. If both
norm and multiplier are specified, then the field vectors
are first normalized before being scaled by the multiplier value.
Examples: diskarray.mif, exchspring.mif,
imageatlas.mif, spinvalve.mif.
- Oxs_ScriptVectorField:
- Conceptually similar to the
Oxs_ScriptScalarField scalar
field object,
except that the script should return a vector (as a 3 element list)
rather than a scalar. In addition to the parameters accepted by
Oxs_ScriptScalarField, Oxs_ScriptVectorField also accepts
an optional parameter norm. If specified, the return
values from the script are size adjusted to the specified magnitude.
If both norm and multiplier are specified, then
the field vectors are first normalized before being scaled by the
multiplier value.
The following example produces a vortex-like unit vector field, with
an interior core region pointing parallel to the z-axis. Here the
scaling region is specified using an atlas reference to an
object named ``:atlas'', which is presumed to be defined earlier in
the MIF file. See the Oxs_ScriptScalarField sample Specify
block for an example using the explicit range option.
proc Vortex { xrel yrel zrel } {
set xrad [expr {$xrel-0.5}]
set yrad [expr {$yrel-0.5}]
set normsq [expr {$xrad*$xrad+$yrad*$yrad}]
if {$normsq <= 0.025} {return "0 0 1"}
return [list [expr {-1*$yrad}] $xrad 0]
}
Specify Oxs_ScriptVectorField {
script Vortex
norm 1
atlas :atlas
}
See also the
Oxs_MaskVectorField
documentation and the discussion of the
ReadFile MIF extension command
for other example uses of the Oxs_ScriptVectorField class.
Examples: cgtest.mif, ellipsoid.mif,
manyregions-scriptfields.mif, sample-vecreflect.mif,
stdprob3.mif, yoyo.mif.
- Oxs_FileVectorField:
- Provides a file-specified vector field. The Specify block has the form
-
Specify Oxs_FileVectorField {
- file filename
- atlas atlas_spec
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- spatial_scaling {
xscale yscale zscale
}
- spatial_offset {
xoff yoff zoff
}
- exterior ext_flag
- norm magnitude
- multiplier mult
- }
Required values in the Specify block are the name of the input vector
field file and the desired scaling parameters. The filename is
specified via the file entry, which names a file
containing a vector field in one of the formats recognized by
avf2ovf. If
atlas or xrange/yrange/zrange are specified,
then the file will be scaled and translated as necessary to fit that
scaling region, in the same manner as done, for example, by
the Oxs_ScriptScalarField and
Oxs_ScriptVectorField classes.
Alternatively, one may specify spatial_scaling and
spatial_offset directly. In this case the vector spatial
positions are taken as specified in the file, multiplied
component-wise by (xscale,yscale,zscale), and then translated by
(xoff,yoff,zoff). If you want to use the spatial coordinates as
directly specified in the file, use (1,1,1) for spatial_scaling
and (0,0,0) for spatial_offset.
In all cases, once the input field has been scaled and translated, it
is then sub-sampled (zeroth-order fit) as necessary to match the
simulation mesh.
The exterior flag determines the behavior at ``exterior
points'', i.e., locations (if any) in the simulation mesh that lie
outside the extent of the scaled and translated vector field. The
ext_flag should be either a three-vector, or one of the
keywords boundary or error. If a three-vector is given,
then that value is supplied at all exterior points. If
ext_flag is set to boundary, then the value used is
the point on the boundary of the input vector field that is closest
to the exterior point. The default setting for ext_flag is
error, which raises an error if there are any exterior points.
The magnitude of the field can be modified by the optional
norm and multiplier attributes. If the norm
parameter is given, then each vector in the field will be
renormalized to the specified magnitude. If the multiplier parameter
is given, then each vector in the field will be multiplied by the
given scalar value. If the multiplier value is negative, the field
direction will be reversed. If both norm and multiplier
are given, then the field vectors are renormalized before being
scaled by the multiplier value.
Examples: stdprob3.mif, yoyo.mif.
- Oxs_RandomVectorField:
- Similar to
Oxs_RandomScalarField, but defines a vector field rather than a scalar field that
varies spatially in a random fashion. The Specify block has the form:
-
Specify Oxs_RandomVectorField {
- min_norm minvalue
- max_norm maxvalue
- cache_grid mesh_spec
- }
The Specify block takes two required parameters, min_norm
and max_norm. The vectors produced will have magnitude
between these two specified values. If min_norm = max_norm,
then the samples are uniformly distributed on the sphere of that radius.
Otherwise, the samples are uniformly distributed in the hollow spherical
volume with inner radius min_norm and outer radius max_norm.
There is also an optional parameter, cache_grid, which takes
a mesh specification that describes the grid used for cache spatial
discretization. If cache_grid is not specified, then each
call to Oxs_RandomVectorField generates a different field. If you
want to use the same random vector field in two places (as a base for
setting, say anisotropy axes and initial magnetization), then specify
cache_grid with the appropriate (usually the base problem)
mesh.
Examples: diskarray.mif, sample2.mif, randomshape.mif
stdprob1.mif.
- Oxs_PlaneRandomVectorField:
- Similar to Oxs_RandomVectorField, except that samples are
drawn from 2D planes rather than 3-space. The Specify block has the
form
-
Specify Oxs_RandomVectorField {
- plane_normal vector_field_spec
- min_norm minvalue
- max_norm maxvalue
- cache_grid mesh_spec
- }
The min_norm, max_norm, and
cache_grid parameters have the same meaning as for the
Oxs_RandomVectorField class. The additional parameter,
plane_normal, specifies a vector field that at each point
provides a vector that is orthogonal to the plane from which the
random vector at that point is to be drawn. If the vector field is
specified explicitly as three real values, then a spatially uniform
vector field is produced and all the random vectors will lie in the
same plane. More generally, however, the normal vectors (and
associated planes) may vary from point to point. As a special case,
if a normal vector at a point is the zero vector, then no planar
restriction is made and the resulting random vector is drawn uniformly
from a hollow ball in three space satisfying the minimum/maximum norm
constraints.
Example:
sample2.mif.
- Oxs_ScriptOrientVectorField:
- This class is analogous to the
Oxs_ScriptOrientScalarField
class.
The Specify block has the form:
-
Specify Oxs_ScriptOrientVectorField:name {
- field vector_field_spec
- script Tcl_script
- script_args { args_request }
- atlas atlas_spec
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- }
The interpretation of the specify block and the operation of the Tcl script is exactly the same as for the Oxs_ScriptOrientScalarField
class, except the input field and the resulting field are
vector fields instead of scalar fields.
Note that the ``orientation'' transformation is applied to the import
spatial coordinates only, not the output vector. For example, if the
field value represents a shaped vector field, and the script
proc is a rotation transformation, then the resulting vector field shape
will be rotated as compared to the original vector field, but the output
vectors themselves will still point in their original directions. In such
cases one may wish to compose the Oxs_ScriptOrientVectorField with
a Oxs_ScriptVectorField
object to rotate the
output vectors as well. This situation occurs also with the
Oxs_AffineOrientVectorField class. See the
Oxs_AffineTransformVectorField
class documentation for an
example illustrating the composition of an object of that class with a
Oxs_AffineOrientVectorField
object.
Example:
sample-vecreflect.mif.
- Oxs_AffineOrientVectorField:
- This class is analogous to the
Oxs_AffineOrientScalarField
class.
The Specify block has the form:
-
Specify Oxs_AffineOrientVectorField {
- field vector_field_spec
- M
{ matrix_entries ... }
- offset {
offx
offy
offz }
- inverse invert_flag
- inverse_slack slack
- }
The interpretation of the specify block and the affine transformation
is exactly the same as for the Oxs_AffineOrientScalarField
class, except the input field and the resulting field are
vector fields instead of scalar fields.
As explained in the
Oxs_ScriptOrientVectorField
documentation, the ``orientation'' transformation is applied to the
import spatial coordinates only, not the output vector. If one wishes
to rotate the output vectors, then a
Oxs_AffineTransformVectorField
object may be applied with the opposite rotation. See that section for
an example.
Examples: yoyo.mif, sample-vecrotate.mif.
- Oxs_AffineTransformVectorField:
- This class applies an affine transform to the output of a vector field.
It is similar to the
Oxs_AffineTransformScalarField
class, except
that in this case the affine transform is applied to a vector instead of
a scalar. The Specify block has the form:
-
Specify Oxs_AffineTransformVectorField {
- field vector_field_spec
- M
{ matrix_entries ... }
- offset {
offx
offy
offz }
- inverse invert_flag
- inverse_slack slack
- }
Because the output from field is a 3-vector, the transform
defined by M and offset requires M to be a
3x3 matrix and offset to be a 3-vector.
Thus, if
v(x) represents the
vector field specified by the field value, then the resulting
vector field is
M.v(x) + off.
M is described by a list of from one to nine entries, in exactly
the same manner as for the
Oxs_AffineOrientVectorField
and
Oxs_AffineOrientScalarField
classes. The
interpretation of offset, inverse, and
inverse_slack is also the same. In particular, if
invert_flag is 1, then the resulting vector field is
M-1. v(x) - off
v(x) - off .
.
The following example illustrates combining a
Oxs_AffineTransformVectorField with a
Oxs_AffineOrientVectorField
to completely rotate a vector field.
Specify Oxs_BoxAtlas:atlas {
xrange {-80e-9 80e-9}
yrange {-80e-9 80e-9}
zrange {0 40e-9}
}
proc Trap { x y z } {
if {$y<=$x && $y<=0.5} {return [list 0 1 0]}
return [list 0 0 0]
}
Specify Oxs_ScriptVectorField:trap {
script Trap
atlas :atlas
}
Specify Oxs_AffineOrientVectorField:orient {
field :trap
M { 0 -1 0
1 0 0
0 0 1 }
offset { -20e-9 0 0 }
inverse 1
}
Specify Oxs_AffineTransformVectorField:rot {
field :orient
M { 0 -1 0
1 0 0
0 0 1 }
}
proc Threshold { vx vy vz } {
set magsq [expr {$vx*$vx+$vy*$vy+$vz*$vz}]
if {$magsq>0} {return 8e5}
return 0.0
}
Specify Oxs_ScriptScalarField:Ms {
vector_fields :rot
script Threshold
script_args vectors
}
Specify Oxs_TimeDriver {
m0 :rot
Ms :Ms
stopping_dm_dt 0.01
evolver :evolve
mesh :mesh
}
The base field here is given by the Oxs_ScriptVectorField:trap
object, which produces a vector field having a trapezoidal shape with
the non-zero vectors pointing parallel to the y-axis. The
:orient and :rot transformations rotate the shape and the
vectors counterclockwise 90 degrees.
Additionally, the offset option in :orient translates the
shape 20 nm towards the left. The original and transformed fields are
illustrated below.
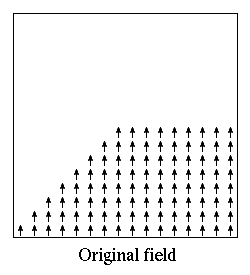
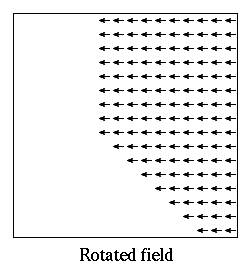
Example:
sample-vecrotate.mif.
- Oxs_MaskVectorField:
- Multiplies a vector field pointwise by a scalar vector field (the mask)
to produce a new vector field. The Specify block has the form:
-
Specify Oxs_MaskVectorField {
- mask scalar_field_spec
- field vector_field_spec
- }
This functionality can be achieved, if in a somewhat more complicated
fashion, with the
Oxs_ScriptVectorField
class. For example, given a scalar field :mask and a vector field
:vfield, this example using the Oxs_MaskVectorField class
Specify Oxs_MaskVectorField {
mask :mask
field :vfield
}
is equivalent to this example using the Oxs_ScriptVectorField
class
proc MaskField { m vx vy vz } {
return [list [expr {$m*$vx}] [expr {$m*$vy}] [expr {$m*$vz}]]
}
Specify Oxs_ScriptVectorField {
script MaskField
script_args {scalars vectors}
scalar_fields { :mask }
vector_fields { :vfield }
}
Of course, the Oxs_ScriptVectorField approach is easily
generalized to much more complicated and arbitrary combinations of
scalar and vector fields.
Example:
rotatecenterstage.mif.
- Oxs_ImageVectorField:
- This class creates a vector field using an image. The Specify block has
the form
-
Specify Oxs_ImageVectorField:name {
- image pic
- multiplier mult
- vx_multiplier xmult
- vy_multiplier ymult
- vz_multiplier zmult
- vx_offset xoff
- vy_offset yoff
- vz_offset zoff
- norm norm_magnitude
- viewplane view
- atlas atlas_spec
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- exterior ext_flag
- }
The image is interpreted as a three-color map, yielding a
vector field where each (x,y,z) component is determined by the red,
green, and blue color components, respectively....
The viewplane, atlas,
xrange/yrange/zrange, and exterior are treated
the same as for the
Oxs_ImageScalarField class
Examples: NONE.
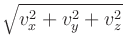 .
.
![]() F(x) - off
F(x) - off![]() /mult,
provided mult is non-zero.
/mult,
provided mult is non-zero.

