- Oxs_BoxAtlas:
- An axes parallel rectangular parallelepiped,
containing a single region that is coterminous with the atlas itself.
The specify block has the form
-
Specify Oxs_BoxAtlas:atlasname {
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- name regionname
- }
where xmin, xmax, ... are coordinates in meters, specifying
the extents of the volume being defined. The regionname label
specifies the name assigned to the region contained in the atlas. The
name entry is optional; if not specified then the
region name is taken from the object instance name, i.e.,
atlasname.
Examples: sample.mif, cgtest.mif.
- Oxs_ImageAtlas:
-
This class is designed to allow an image file
to be used to define regions in terms of colors in the image. It is
intended for use in conjunction with the Oxs_AtlasScalarField and
Oxs_AtlasVectorField classes in circumstances where a small
number of distinct species (materials) are being modeled. This provides
a generalization of the mask file
functionality of the 2D solver
(Sec. 17.1.3).
For situations requiring continuous variation in material parameters,
the script field classes should be used in conjunction with the
ReadFile MIF extension command. See the
ColorField sample proc in the ReadFile
documentation for an example of this
technique.
The Oxs_ImageAtlas Specify block has the following form:
-
Specify Oxs_ImageAtlas:name {
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- viewplane view
- image pic
- colormap {
- color-1 region_name
- color-2 region_name
- ...
- color-n region_name
}
- matcherror max_color_distance
- }
The xrange, yrange, zrange entries
specify the extent of the atlas, in meters. The viewplane
view value should be one of the three two-letter codes xy,
zx or yz, which specify the mapping of the horizontal and
vertical axes of the image respectively to axes in the simulation. The
image is scaled as necessary along each dimension to match the atlas
extents along the corresponding axes. The image is overlaid through the
entire depth of the perpendicular dimension, i.e., along the axis absent
from the viewplane specification. The
Oxs_ImageAtlas class can be used inside a
Oxs_MultiAtlas object to specify regions in a multilayer
structure.
The image entry specifies the name of the image file to use.
If the file path is relative, then it will be taken with respect to the
directory containing the MIF file. The image format may be any of
those recognized by any2ppm. The file will be read directly by Oxs if it is
in the P3 or P6 PPM formats, otherwise any2ppm will be
automatically launched to perform the conversion.
The colormap value is an even length list of color + region
name pairs. The colors may be specified in any of several ways. The
most explicit is to use one of the Tk numeric formats,
#rgb, #rrggbb, #rrrgggbbb or #rrrrggggbbbb, where
each r, g, and b is one hex digit (i.e., 0-9 or A-F) representing the
red, green and blue components of the color, respectively. For example,
#F00 is bright (full-scale) red, #800 would be a darker red, while
#FF0 and #FFFF00 would both be bright yellow. Refer to the
Tk_GetColor documentation for details. For shades of gray the
special notation grayD or greyD is available, where D is a
decimal value between 0 and 100, e.g., grey0 is black and
grey100 is white. Alternatively, one may use any of the symbolic
names defined in the oommf/config/colors.config file, such as
red, white and skyblue. When comparing symbolic names,
spaces and capitalization are ignored. The list of symbolic names can
be extended by adding additional files to the Color filename option
in the options.tcl customization file. Finally, one color in the
colormap list may optionally be the special keyword ``default''.
All pixels that don't match any of the other specified colors (as
determined by the matcherror option) are assigned to region
paired with default.
Each of the specified colors should be distinct, but the region names
are allowed to be repeated as desired. The region names may be chosen
arbitrarily, except the special keyword ``universe'' is reserved for
points not in any of the regions. This includes all points outside the
atlas bounding box defined by the xrange, yrange, zrange
entries, but may also include points inside that boundary.
Pixels in the image are assigned to regions by comparing the color of
the pixel to the list of colors specified in colormap. If the
pixel color is closer to a colormap color than
max_color_distance, then the colors are considered matched.
If a pixel color matches exactly one colormap color, then the pixel
is assigned to the corresponding region. If a pixel color matches more
than one colormap color, the pixel is assigned to the region
corresponding to the closest match. If a pixel color doesn't match any
of the colormap colors, then it is assigned to the default
region, which is the region paired with the ``default'' keyword. If
default does not explicitly appear in the colormap colors
list, then universe is made the default region.
To calculate the distance between two colors, each color is first
converted to a scaled triplet of floating point red, green, and blue
values, (r, g, b), where each component lies in the interval [0, 1],
with (0, 0, 0) representing black and (1, 1, 1) representing white. For
example, (0, 0, 1) is bright blue. Given two colors in this
representation, the distance is computed using the standard Euclidean
norm with uniform weights, i.e., the distance between
(r1, g1, b1)
and
(r2, g2, b2) and is
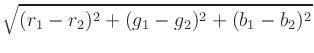 .
.
Since the difference in any one component is at most 1, the distance
between any two colors is at most
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\sqrt{3}\\ \rule{1pt}{0pt}\end{array}$}$](img4.gif) .
.
As explained above, two colors are considered to match if the distance
between them is less than the specified matcherror value. If
max_color_distance is sufficiently small, then it may easily
happen that a pixel's color does not match any of the specified region
colors, so the pixel would be assigned to the default region. On the
other hand, if max_color_distance is larger than
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\sqrt{3}\\ \rule{1pt}{0pt}\end{array}$}$](img4.gif) , then all colors will match, and no pixels will be
assigned to the default region. If matcherror is not specified,
then the default value for max_color_distance is 3, which
means all colors match.
, then all colors will match, and no pixels will be
assigned to the default region. If matcherror is not specified,
then the default value for max_color_distance is 3, which
means all colors match.
The following example should help clarify these matters.
Specify Oxs_ImageAtlas:atlas {
xrange { 0 400e-9 }
yrange { 0 200e-9 }
zrange { 0 20e-9 }
image mypic.gif
viewplane "xy"
colormap {
blue cobalt
red permalloy
green universe
default cobalt
}
matcherror .1
}
Blue pixels get mapped to the ``cobalt'' region and red pixels
to the ``permalloy'' region. Green pixels are mapped to the
``universe'' non-region, which means they are considered to be outside
the atlas entirely. This is a fine point, but comes into
play when atlases with overlapping bounding boxes are brought together
inside an Oxs_MultiAtlas. To which region would an orange pixel
be assigned? The scaled triplet representation for orange is
(1, 0.647, 0), so the distance to blue is 1.191, the distance to red
is 0.647, and the distance to green is 1.06. Thus the closest color
is red, but 0.647 is outside the matcherror setting of 0.1, so
orange doesn't match any of the colors and is hence assigned to the
default region, which in this case is cobalt. On the other hand, if
matcherror had been set to say 1, then orange and red would match
and orange would be assigned to the permalloy region.
Pixels with colors that are equidistant to and match more than one color
in the colormap will be assigned to one of the closest color regions.
The user should not rely on any particular selection, that is to say,
the explicit matching procedure in this case is not defined.
Examples: imageatlas.mif, grill.mif.
- Oxs_MultiAtlas:
- This atlas is built up as an ordered list of
other atlases. The set of regions defined by the Oxs_MultiAtlas
is the union of the regions of all the atlases contained therein. The
sub-atlases need not be disjoint, however each point is assigned to the
region in the first sub-atlas in the list that contains it, so the
regions defined by the Oxs_MultiAtlas are effectively disjoint.
The Oxs_MultiAtlas specify block has the form
-
Specify Oxs_MultiAtlas:name {
- atlas atlas_1_spec
- atlas atlas_2_spec
- ...
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- }
Each atlas_spec may be either a reference to an atlas defined
earlier and outside the current Specify block, or else an inline,
embedded atlas definition. The bounding box xrange,
yrange and zrange specifications are each
optional. If not specified the corresponding range for the atlas
bounding box is taken from the minimal bounding box containing all the
sub-atlases.
If the atlases are not disjoint, then the regions as defined by an
Oxs_MultiAtlas can be somewhat different from those of the
individual component atlases. For example, suppose regionA is a
rectangular region in atlasA with corner points (5,5,0) and
(10,10,10), and regionB is a rectangular region in atlasB with
corner points (0,0,0) and (10,10,10). When composed in the order
atlasA, atlasB inside an Oxs_MultiAtlas, regionA
reported by the Oxs_MultiAtlas will be the same as regionA
reported by atlasA, but regionB as reported by the
Oxs_MultiAtlas will be the ``L'' shaped volume of those points in
atlasB's regionB not inside regionA. If the
Oxs_MultiAtlas is constructed with atlasB first and
atlasA second, then regionB as reported by the
Oxs_MultiAtlas would agree with that reported by atlasB, but
regionA would be empty.
NOTE: The attributes key label
is not supported by this
class.
Examples: manyregions-multiatlas.mif, spinvalve.mif,
spinvalve-af.mif, yoyo.mif.
- Oxs_ScriptAtlas:
- An atlas where the regions are defined via a Tcl script. The specify
block has the form
-
Specify Oxs_ScriptAtlas:name {
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- regions {
rname_1 rname_2 ... rname_n
}
- script_args { args_request }
- script Tcl_script
- }
Here xmin, xmax, ... are coordinates in meters, specifying
the extents of the axes-parallel rectangular parallelepiped enclosing
the total volume being identified. This volume is subdivided
into n sub-regions, using the names as given in the
regions list. The script is used to assign
points to the various regions. Appended to the script are the arguments
requested by script_args, in the manner explained in the
User Defined Support Procedures section of the
MIF 2 file format documentation. The value args_request
should be a subset of {relpt rawpt minpt maxpt span }. If
script_args is not specified, the default value relpt is
used. When executed, the return value from the script should be an
integer in the range 1 to n, indicating the user-defined region in
which the point lies, or else 0 if the point is not in any
of the n regions. Region index 0 is reserved for the implicit
``universe'' region, which is all-encompassing. The following example
may help clarify the discussion:
proc Octs { cellsize x y z xmin ymin zmin xmax ymax zmax } {
set xindex [expr {int(floor(($x-$xmin)/$cellsize))}]
set yindex [expr {int(floor(($y-$ymin)/$cellsize))}]
set zindex [expr {int(floor(($z-$zmin)/$cellsize))}]
set octant [expr {1+$xindex+2*$yindex+4*$zindex}]
if {$octant<1 || $octant>8} {
return 0
}
return $octant
}
Specify Oxs_ScriptAtlas:octant {
xrange {-20e-9 20e-9}
yrange {-20e-9 20e-9}
zrange {-20e-9 20e-9}
regions { VIII V VII VI IV I III II }
script_args { rawpt minpt maxpt }
script { Octs 20e-9 }
}
This atlas divides the rectangular volume between
(- 20, - 20, - 20) and
(20, 20, 20) (nm) into eight regions, corresponding to the standard
octants, I through VIII. The Octs Tcl procedure returns a
value between 1 and 8, with 1 corresponding to octant VIII and 8 to
octant II. The canonical octant ordering starts with I as the
+ x, + y, + z space, proceeds counterclockwise in the + z half-space, and
concludes in the - z half-space with V directly beneath I, VI beneath
II, etc. The ordering computed algorithmically in Octs
starts with 1 for the - x, - y, - z space, 2 for the + x, - y, - z space, 3
for the - x, + y, - z space, etc. The conversion between the two systems
is accomplished by the ordering of the regions list.
Examples: manyregions-scriptatlas.mif, octant.mif,
tclshapes.mif, diskarray.mif, ellipsoid-atlasproc.mif.
- Oxs_EllipsoidAtlas:
- Defines an ellipsoidal region with axes parallel to the coordinate
axes. This functionality can be obtained using the
Oxs_ScriptAtlas class with an appropriate Tcl script, but this
class is somewhat easier to use and faster. The Specify
block has the form
-
Specify Oxs_EllipsoidAtlas:atlasname {
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- name regionname
- }
Here xmin, xmax, ... are coordinates in meters, specifying
the bounding box for the ellipsoid. The layout of the Specify
block is exactly the same as for the Oxs_BoxAtlas class, except
that in this case the named region is not the whole bounding box but
rather that subvolume that is the interior of the ellipsoid inscribed
inside the bounding box. Points exterior to that ellipsoid are
assigned to the ``universe'' region.
As in the Oxs_BoxAtlas case, the regionname entry is
optional; if missing, the region name is taken from the object instance
name, i.e., atlasname.
Example: ellipsoid.mif. See also
ellipsoid-atlasproc.mif and ellipsoid-fieldproc.mif for
equivalent examples using Tcl scripts.
- Oxs_EulerEvolve:
- Time evolver implementing a simple first order forward Euler method with
step size control on the Landau-Lifshitz
ODE [10,12]:
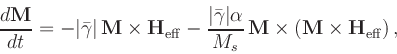 |
(2) |
where
M is the magnetization,
Heff is the effective
field,
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\bar{\gamma}\\ \rule{1pt}{0pt}\end{array}$}$](img22.gif) is the Landau-Lifshitz gyromagnetic ratio, and
is the Landau-Lifshitz gyromagnetic ratio, and
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\alpha\\ \rule{1pt}{0pt}\end{array}$}$](img24.gif) is the damping constant. The Gilbert form
is the damping constant. The Gilbert form
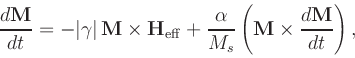 |
(3) |
where
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\gamma\\ \rule{1pt}{0pt}\end{array}$}$](img27.gif) is the Gilbert gyromagnetic ratio, is
mathematically equivalent to the Landau-Lifshitz form under the
relation
is the Gilbert gyromagnetic ratio, is
mathematically equivalent to the Landau-Lifshitz form under the
relation
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\gamma = (1+\alpha^2)\,\bar{\gamma}\\ \rule{1pt}{0pt}\end{array}$}$](img29.gif) .
.
The Specify block has the form
-
Specify Oxs_EulerEvolve:name {
- alpha
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\alpha\\ \rule{1pt}{0pt}\end{array}$}$](img24.gif)
- gamma_LL
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\bar{\gamma}\\ \rule{1pt}{0pt}\end{array}$}$](img22.gif)
- gamma_G
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\gamma\\ \rule{1pt}{0pt}\end{array}$}$](img27.gif)
- do_precess precess
- min_timestep minimum_stepsize
- max_timestep maximum_stepsize
- fixed_spins {
- atlas_spec
- region1 region2 ...
- }
- start_dm
 m
m
- error_rate rate
- absolute_step_error abs_error
- relative_step_error rel_error
- step_headroom headroom
- }
All the entries have default values, but the ones most commonly adjusted
are listed first.
The options alpha, gamma_LL and
gamma_G are as in the Landau-Lifshitz-Gilbert ODE
(2), (3), where the units on
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\bar{\gamma}\\ \rule{1pt}{0pt}\end{array}$}$](img22.gif) and
and
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\gamma\\ \rule{1pt}{0pt}\end{array}$}$](img27.gif) are m/A . s and
are m/A . s and
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\alpha\\ \rule{1pt}{0pt}\end{array}$}$](img24.gif) is dimensionless. At most one of
is dimensionless. At most one of
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\bar{\gamma}\\ \rule{1pt}{0pt}\end{array}$}$](img22.gif) and
and
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\gamma\\ \rule{1pt}{0pt}\end{array}$}$](img27.gif) should be specified. If
neither is specified, then the default is
should be specified. If
neither is specified, then the default is
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\gamma\\ \rule{1pt}{0pt}\end{array}$}$](img27.gif) = 2.211 x 105.
(Because of the absolute value convention adopted on
= 2.211 x 105.
(Because of the absolute value convention adopted on
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\bar{\gamma}\\ \rule{1pt}{0pt}\end{array}$}$](img22.gif) and
and
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\gamma\\ \rule{1pt}{0pt}\end{array}$}$](img27.gif) in
(2), (3), the sign given to the value of
gamma_LL or gamma_G in the Specify block is
irrelevant.) The default value for
in
(2), (3), the sign given to the value of
gamma_LL or gamma_G in the Specify block is
irrelevant.) The default value for
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\alpha\\ \rule{1pt}{0pt}\end{array}$}$](img24.gif) is 0.5, which is
large compared to experimental values, but allows simulations to
converge to equilibria in a reasonable time. However, for accurate
dynamic studies it is important to assign an appropriate value to
is 0.5, which is
large compared to experimental values, but allows simulations to
converge to equilibria in a reasonable time. However, for accurate
dynamic studies it is important to assign an appropriate value to
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\alpha\\ \rule{1pt}{0pt}\end{array}$}$](img24.gif) .
.
The do_precess value should be either 1 or 0, and determines
whether or not the precession term in the Landau-Lifshitz ODE (i.e., the
first term on the righthand side in (2)) is used. If
precess is 0, then precession is disabled and the simulation
evolves towards equilibrium along a steepest descent path. The default
value is 1.
The min_timestep and max_timestep parameters provide
soft limits on the size of steps taken by the evolver. The minimum
value may be overridden by the driver if a smaller step is needed to
meet time based stopping criteria. The maximum value will be ignored if
a step of that size would produce a magnetization state numerically
indistinguishable from the preceding state. The units for
min_timestep and max_timestep are seconds. Default
values are 0 and 10-10 respectively.
The optional fixed_spins entry allows the magnetization in
selected regions of the simulation to be frozen in its initial
configuration. The value portion of the entry should be a list, with
the first element of the list being either an inline atlas definition
(grouped as a single item), or else the name of a previously defined
atlas. The remainder of the list are names of regions in that atlas for
which the magnetization is to be be fixed, i.e.,
M(t) = M(0) for all
time t for all points in the named regions. Fields and energies are
computed and reported normally across these regions. Although any atlas
may be used, it is frequently convenient to set up an atlas with special
regions defined expressly for this purpose.
The stepsize for the first candidate iteration in the problem run is
selected so that the maximum change in the normalized (i.e., unit)
magnetization
m is the value specified by start_dm. The
units are degrees, with default value 0.01.
The four remaining entries, error_rate,
absolute_step_error, relative_step_error, and
step_headroom, control fine points of stepsize selection,
and are intended for advance use only. Given normalized magnetization
mi(t) at time t and position i, and candidate magnetization
mi(t + 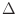 t) at time
t +
t) at time
t + 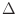 t, the error at position i is
estimated to be
t, the error at position i is
estimated to be
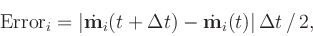
where the derivative with respect to time,
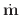 , is computed
using the Landau-Lifshitz ODE (2). First order methods
essentially assume that
, is computed
using the Landau-Lifshitz ODE (2). First order methods
essentially assume that
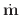 is constant on the interval
[t, t +
is constant on the interval
[t, t + 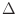 t]; the above formula uses the difference in
t]; the above formula uses the difference in
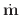 at the endpoints of the interval to estimate (guess) how untrue that
assumption is.
at the endpoints of the interval to estimate (guess) how untrue that
assumption is.
A candidate step is accepted if the maximum error across all positions
i is smaller than absolute_step_error,
error_rate
x 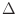 t, and
relative_step_error
x |
t, and
relative_step_error
x |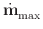 |
|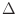 t, where
|
t, where
|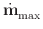 | is the maximum value of
|
| is the maximum value of
|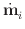 | across all i at time t. If the step is rejected,
then a smaller stepsize is computed that appears to pass the above
tests, and a new candidate step is proposed using that smaller stepsize
times step_headroom. Alternatively, if the step is accepted,
then the error information is used to determine the stepsize for the
next step, modified in the same manner by step_headroom.
| across all i at time t. If the step is rejected,
then a smaller stepsize is computed that appears to pass the above
tests, and a new candidate step is proposed using that smaller stepsize
times step_headroom. Alternatively, if the step is accepted,
then the error information is used to determine the stepsize for the
next step, modified in the same manner by step_headroom.
The error calculated above is in terms of unit magnetizations, so the
natural units are radians or radians/second. Inside the Specify block,
however, the error_rate and absolute_step_error are
specified in degrees/nanosecond and degrees, respectively; they are
converted appropriately inside the code before use. The
relative_step_error is a dimensionless quantity, representing a
proportion between 0 and 1. The error check controlled by each of these
three quantities may be disabled by setting the quantity value to -1.
They are all optional, with default values of -1 for error_rate,
0.2 for absolute_step_error, and 0.2 for
relative_step_error.
The headroom quantity should lie in the range (0, 1), and controls
how conservative the code will be in stepsize selection. If headroom
is too large, then much computation time will be lost computing
candidate steps that fail the error control tests. If headroom is
small, then most candidate steps will pass the error control tests, but
computation time may be wasted calculating more steps than are
necessary. The default value for headroom is 0.85.
In addition to the above error control tests, a candidate step will also
be rejected if the total energy, after adjusting for effects due to any
time varying external field, is found to increase. In this case the
next candidate stepsize is set to one half the rejected stepsize.
The Oxs_EulerEvolve module provides five scalar, one scalar
field, and three vector field outputs. The scalar outputs are
- Max dm/dt: maximum
| dm/dt|, in degrees per
nanosecond;
m is the unit magnetization direction.
- Total energy: in joules.
- Delta E: change in energy between last step and current
step, in joules.
- dE/dt: derivative of energy with respect to time, in
joules per second.
- Energy calc count: number of times total energy has been
calculated.
The scalar field output is
- Total energy density: cellwise total energy density, in
J/m3.
The vector field outputs are
- Total field: total effective field
H in A/m.
- mxH: torque in A/m;
m is the unit magnetization
direction,
H is the total effective field.
- dm/dt: derivative of spin
m with respect to time, in
radians per second.
Example: octant.mif.
- Oxs_RungeKuttaEvolve:
- Time evolver implementing several Runge-Kutta methods for integrating
the Landau-Lifshitz-Gilbert ODE
(2), (3), with step size control. In
most cases it will greatly outperform the Oxs_EulerEvolve class.
The Specify block has the form
-
Specify Oxs_RungeKuttaEvolve:name {
- alpha
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\alpha\\ \rule{1pt}{0pt}\end{array}$}$](img24.gif)
- gamma_LL
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\bar{\gamma}\\ \rule{1pt}{0pt}\end{array}$}$](img22.gif)
- gamma_G
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\gamma\\ \rule{1pt}{0pt}\end{array}$}$](img27.gif)
- do_precess precess
- allow_signed_gamma signed_gamma
- min_timestep minimum_stepsize
- max_timestep maximum_stepsize
- fixed_spins {
- atlas_spec
- region1 region2 ...
- }
- start_dm
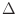 m
m
- start_dt start_timestep
- stage_start scontinuity
- error_rate rate
- absolute_step_error abs_error
- relative_step_error rel_error
- energy_precision eprecision
- min_step_headroom min_headroom
- max_step_headroom max_headroom
- reject_goal reject_proportion
- method subtype
- }
Most of these options appear also in the
Oxs_EulerEvolve class.
The repeats have the same meaning as in that class, and the same
default values except for relative_step_error and
error_rate, which for Oxs_RungeKuttaEvolve have the
default values of 0.01 and 1.0, respectively. Additionally, the
alpha, gamma_LL and gamma_G options
may be initialized using scalar field objects, to allow these material
parameters to vary spatially.
The allow_signed_gamma parameter is for simulation testing
purposes, and is intended for advanced use only. There is some lack of
consistency in the literature with respect to the sign of
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\gamma\\ \rule{1pt}{0pt}\end{array}$}$](img27.gif) . For this reason the Landau-Lifshitz-Gilbert
equations are presented above (2, 3)
using the absolute value of
. For this reason the Landau-Lifshitz-Gilbert
equations are presented above (2, 3)
using the absolute value of
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\gamma\\ \rule{1pt}{0pt}\end{array}$}$](img27.gif) . This is the
interpretation used if allow_signed_gamma is 0 (the default). If
instead allow_signed_gamma is set to 1, then the
Landau-Lifshitz-Gilbert equations are interpreted without the absolute
values and with a sign change on the
. This is the
interpretation used if allow_signed_gamma is 0 (the default). If
instead allow_signed_gamma is set to 1, then the
Landau-Lifshitz-Gilbert equations are interpreted without the absolute
values and with a sign change on the
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\gamma\\ \rule{1pt}{0pt}\end{array}$}$](img27.gif) terms, i.e., the
default value for
terms, i.e., the
default value for
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\gamma\\ \rule{1pt}{0pt}\end{array}$}$](img27.gif) in this case is
-2.211 x 105 (units are m/A . s). In this setting, if
in this case is
-2.211 x 105 (units are m/A . s). In this setting, if
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\gamma\\ \rule{1pt}{0pt}\end{array}$}$](img27.gif) is set positive then the spins will precess backwards about the
effective field, and the damping term will force the spins away
from the effective field and increase the total energy. If you are
experimenting with
is set positive then the spins will precess backwards about the
effective field, and the damping term will force the spins away
from the effective field and increase the total energy. If you are
experimenting with
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\gamma>0\\ \rule{1pt}{0pt}\end{array}$}$](img35.gif) , you should either set
, you should either set
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\alpha<=0\\ \rule{1pt}{0pt}\end{array}$}$](img36.gif) to force spins back towards the effective field,
or disable the energy precision control (discussed
below).
to force spins back towards the effective field,
or disable the energy precision control (discussed
below).
The two controls min_step_headroom (default value 0.33) and
max_step_headroom (default value 0.95) replace the single
step_headroom option in Oxs_EulerEvolve. The effective
step_headroom is automatically adjusted by the evolver between the
min_headroom and max_headroom limits to make the
observed reject proportion approach the reject_goal (default
value 0.05).
The method entry selects a particular Runge-Kutta
implementation. It should be set to one of rk2,
rk4, rkf54, rkf54m, or rkf54s;
the default value is rkf54. The rk2 and
rk4 methods implement canonical second and fourth global order
Runge-Kutta methods[18], respectively. For rk2,
stepsize control is managed by comparing
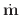 at the middle and
final points of the interval, similar to what is done for stepsize
control for the Oxs_EulerEvolve class. One step of the
rk2 method involves 2 evaluations of
at the middle and
final points of the interval, similar to what is done for stepsize
control for the Oxs_EulerEvolve class. One step of the
rk2 method involves 2 evaluations of
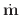 .
.
In the rk4 method, two successive steps are taken at half the
nominal step size, and the difference between that end point and that
obtained with one full size step are compared. The error is estimated at
1/15th the maximum difference between these two states. One step of the
rk4 method involves 11 evaluations of
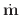 , but the
end result is that of the 2 half-sized steps.
, but the
end result is that of the 2 half-sized steps.
The remaining methods, rkf54, rkf54m,
and rkf54s, are closely related Runge-Kutta-Fehlberg methods
derived by Dormand and Prince[7,8]. In the
nomenclature of these papers,
rkf54 implements RK5(4)7FC,
rkf54m implements RK5(4)7FM, and
rkf54s implements RK5(4)7FS.
All are 5th global order with an embedded 4th order method for stepsize
control. Each step of these methods requires 6 evaluations of
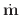 if the step is accepted, 7 if rejected. The difference
between the methods involves tradeoffs between stability and error
minimization. The RK5(4)7FS method has the best stability, RK5(4)7FM
the smallest error, and RK5(4)7FC represents a compromise between the
two. The default method used by Oxs_RungeKuttaEvolve is
RK5(4)7FC.
if the step is accepted, 7 if rejected. The difference
between the methods involves tradeoffs between stability and error
minimization. The RK5(4)7FS method has the best stability, RK5(4)7FM
the smallest error, and RK5(4)7FC represents a compromise between the
two. The default method used by Oxs_RungeKuttaEvolve is
RK5(4)7FC.
The remaining undiscussed entry in the Oxs_RungeKuttaEvolve
Specify block is energy_precision. This should be set to an
estimate of the expected relative accuracy of the energy calculation.
After accounting for any change in the total energy arising from
time-varying applied fields, the energy remainder should decrease from
one step of the LLG ODE to the next. Oxs_RungeKuttaEvolve will
reject a step if the energy remainder is found to increase by more than
that allowed by eprecision. The default value for
eprecision is 1e-10. This control
may be disabled by setting eprecision to -1.
The Oxs_RungeKuttaEvolve module provides the same scalar, scalar
field, and vector field outputs as Oxs_EulerEvolve.
Examples: sample.mif, acsample.mif,
varalpha.mif, yoyo.mif.
- Oxs_SpinXferEvolve:
- Time evolver that integrates an
Landau-Lifshitz-Gilbert ODE augmented with a
spin momentum term [21],
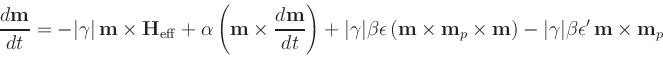 |
(4) |
(compare to (3)), where
| m |
= |
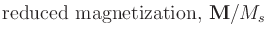 |
|
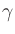 |
= |
Gilbert gyromagnetic ratio |
|
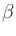 |
= |
 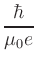  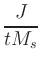 |
|
| mp |
= |
(unit) electron polarization direction |
|
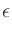 |
= |
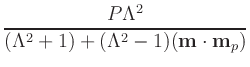 |
|
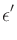 |
= |
secondary spin tranfer term. |
|
In the definition of 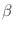 , e is the electron charge in C, J is
current density in A/m2, t is the free layer thickness in meters,
and Ms is the saturation magnetization in A/m.
, e is the electron charge in C, J is
current density in A/m2, t is the free layer thickness in meters,
and Ms is the saturation magnetization in A/m.
The various parameters are defined in the Specify block, which is an
extension of that for the
Oxs_RungeKuttaEvolve class:
-
Specify Oxs_SpinXferEvolve:name {
- alpha
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\alpha\\ \rule{1pt}{0pt}\end{array}$}$](img24.gif)
- gamma_LL
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\bar{\gamma}\\ \rule{1pt}{0pt}\end{array}$}$](img22.gif)
- gamma_G
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\gamma\\ \rule{1pt}{0pt}\end{array}$}$](img27.gif)
- do_precess precess
- allow_signed_gamma signed_gamma
- min_timestep minimum_stepsize
- max_timestep maximum_stepsize
- fixed_spins {
- atlas_spec
- region1 region2 ...
- }
- start_dm
 m
m
- stage_start scontinuity
- error_rate rate
- absolute_step_error abs_error
- relative_step_error rel_error
- energy_precision eprecision
- min_step_headroom min_headroom
- max_step_headroom max_headroom
- reject_goal reject_proportion
- method subtype
- P polarization
- P_fixed p_fixed_layer
- P_free p_free_layer
- Lambda
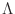
- Lambda_fixed
 _fixed_layer
_fixed_layer
- Lambda_free
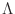 _free_layer
_free_layer
- eps_prime ep
- J current_density
- J_profile Jprofile_script
- J_profile_args Jprofile_script_args
- mp p_direction
- energy_slack eslack
- }
The options duplicated in the
Oxs_RungeKuttaEvolve class
Specify block have the same meaning and default values here, with the
exception of error_rate, which for
Oxs_SpinXferEvolve has the default value of -1 (i.e., disabled).
The default values for P and Lambda are 0.4 and 2,
respectively. If preferred, values for the fixed and free layers may be
instead specified separately, through P_fixed,
P_free, Lambda_fixed, and
Lambda_free. Otherwise P_fixed = P_free = P and
Lambda_fixed = Lambda_free = Lambda. Lambda must be larger than or
equal to 1; set Lambda=1 to remove the dependence of
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\epsilon\\ \rule{1pt}{0pt}\end{array}$}$](img51.gif) on
m . mp. If you want non-zero
on
m . mp. If you want non-zero
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\epsilon^\prime\\ \rule{1pt}{0pt}\end{array}$}$](img53.gif) , it is set directly as
eps_prime.
, it is set directly as
eps_prime.
Current density J and unit polarization direction
mp are required. The units on J are A/m2. Positive J
produces torque that tends to align
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\textbf{m}\\ \rule{1pt}{0pt}\end{array}$}$](img54.gif) towards
towards
![$\mbox{\renewcommand {\arraystretch}{0}$\begin{array}[b]{@{}c@{}}\textbf{m}_p\\ \rule{1pt}{0pt}\end{array}$}$](img55.gif) .
.
Parameters J, mp, P, Lambda, and eps_prime may all be varied pointwise,
but are fixed with respect to time. However, J can be multiplied by a
time varying ``profile,'' to model current rise times, pulses, etc. Use
the J_profile and J_profile_args options to
enable this feature. The Jprofile_script should be a Tcl script that returns a single scalar. Jprofile_script_args
should be a subset of {stage stage_time total_time }, to
specify arguments appended to Jprofile_script on each time
step. Default is the entire set, in the order as listed.
The Oxs_SpinXferEvolve module provides the same five scalar
outputs and three vector outputs as Oxs_RungeKutta, plus the
scalar output ``average J,'' and the vector field outputs ``Spin
torque'' (which is
|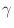 |
|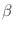
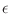
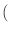 m x mp x m
m x mp x m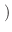 ) and
``J*mp.'' (Development note: In the case propagate_mp is
enabled, mp is actually
) and
``J*mp.'' (Development note: In the case propagate_mp is
enabled, mp is actually
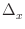
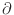 m/
m/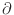 x,
where
x is the flow direction and
x,
where
x is the flow direction and 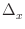 is the cell dimension
in that direction.)
is the cell dimension
in that direction.)
The Oxs_SpinXferEvolve class does not include any oersted
field arising from the current. Of course, arbitrary fields simulating
the oersted field may be added separately as Zeeman energy terms. An
example of this is contained in the spinxfer.mif sample file.
There are no temperature effects in this evolver, i.e., it is a T = 0 K
code.
Note also that
mp is fixed.
For basic usage, the Specify block can be as simple as
Specify Oxs_SpinXferEvolve:evolve {
alpha 0.014
J 7.5e12
mp {1 0 0}
P 0.4
Lambda 2
}
This class is still in early development; at this time the example files
are located in oommf/app/oxs/local instead of
oommf/app/oxs/examples.
Examples: spinxfer.mif, spinxfer-miltat.mif,
spinxfer-onespin.mif.
- Oxs_CGEvolve:
- The minimization evolver is Oxs_CGEvolve, which is an
in-development conjugate gradient minimizer with no preconditioning. The
Specify block has the form
-
Specify Oxs_CGEvolve:name {
- gradient_reset_angle reset_angle
- gradient_reset_count count
- minimum_bracket_step minbrack
- maximum_bracket_step maxbrack
- line_minimum_angle_precision min_prec_angle
- line_minimum_relwidth relwidth
- energy_precision eprecision
- method cgmethod
- fixed_spins {
- atlas_spec
- region1 region2 ...
- }
- }
All entries have default values.
The evolution to an energy minimum precedes by a sequence of line
minimizations. Each line represents a one dimensional affine subspace
in the 3N dimensional space of possible magnetization configurations,
where N is the number of spins in the simulation. Once a minimum has
been found along a line, a new direction is chosen that is ideally
orthogonal to all preceding directions, but related to the gradient of
the energy taken with respect to the magnetization. In practice the
line direction sequence cannot be extended indefinitely; the parameters
gradient_reset_angle and gradient_reset_count
control the gradient resetting process. The first checks the angle
between the new direction and the gradient. If that angle is larger
than reset_angle (expressed in degrees), then the selected
direction is thrown away, and the conjugate-gradient process is
re-initialized with the gradient direction as the new first direction.
In a similar vein, count specifies the maximum number of line
directions selected before resetting the process. Because the first
line in the sequence is selected along the gradient direction, setting
count to 1 effectively turns the algorithm into a steepest
descent minimization method. The default values for
reset_angle and count are 80 degrees and 50,
respectively.
Once a minimization direction has been selected, the first stage of the
line minimization is to bracket the minimum energy on that line, i.e.,
given a start point on the line—the location of the minimum from the
previous line minimization—find another point on the line such that
the energy minimum lies between those two points. As one moves along
the line, the spins in the simulation rotate, with one spin rotating
faster than (or at least as fast as) all the others. If the start point
was not the result of a successful line minimization from the previous
stage, then the first bracket attempt step is sized so that the fastest
moving spin rotates through the angle specified by
minimum_bracket_step. In the more usual case that the
start point is a minimum from the previous line minimization stage, the
initial bracket attempt step size is set to the distance between the
current start point and the start point of the previous line
minimization stage.
The energy and gradient of the energy are examined at the candidate
bracket point to test if an energy minimum lies in the interval. If
not, the interval is extended, based on the size of the first bracket
attempt interval and the derivatives of the energy at the interval
endpoints. This process is continued until either a minimum is
bracketed or the fastest moving spin rotates through the angle specified
by maximum_bracket_step.
If the bracketing process is successful, then a one dimensional
minimization is carried out in the interval, using both energy and
energy derivative information. Each step in this process reduces the
width of the bracketing interval. This process is continued until
the angle between the line direction and the computed energy
gradient is within line_minimum_angle_precision degrees of
orthogonal, and the width of the interval relative to the distance of the
interval from the start point (i.e., the stop point from the previous
line minimization process) is less than
line_minimum_relwidth. The stop point,
i.e., the effective minimum, is taken to be the endpoint of the final
interval having smaller energy. The default value for
min_prec_angle is 1 degree, and the default value for
relwidth is 1. This latter setting effectively disables the
line_minimum_relwidth control, which should generally be used
only as a secondary control.
If the bracketing process is unsuccessful, i.e., the check for bracketed
energy minimum failed at the maximum bracket interval size allowed by
maximum_bracket_step, then the maximum bracket endpoint is
accepted as the next point in the minimization iteration.
Once the line minimum stop point has been selected, the next iteration
begins with selection of a new line direction, as described above,
except in the case where the stop point was not obtained as an actual
minimum, but rather by virtue of satisfying the
maximum_bracket_step constraint. In that case the orthogonal
line sequence is reset, in the same manner as when the
gradient_reset_angle or gradient_reset_count
controls are triggered, and the next line direction is taken directly
from the energy gradient.
There are several factors to bear in mind when selecting values for
the parameters minimum_bracket_step,
maximum_bracket_step, and line_minimum_relwidth.
If minimum_bracket_step is too small, then it may take a
great many steps to obtain an interval large enough to bracket the
minimum. If minimum_bracket_step is too large, then the
bracket interval will be unnecessarily generous, and many steps may be
required to locate the minimum inside the bracketing interval. However,
this value only comes into play when resetting the line minimization
direction sequence, so the setting is seldom critical. It is specified
in degrees, with default value 0.05.
If maximum_bracket_step is too small, then the minima will be
mostly not bracketed, and the minimization will degenerate into a type
of steepest descent method. On the other hand, if
maximum_bracket_step is too large, then the line
minimizations may draw the magnetization far away from a local energy
minimum (i.e., one on the full 3N dimensional magnetization space),
eventually ending up in a different, more distant minimum. The value
for maximum_bracket_step is specified in degrees, with
default value 10.
The line_minimum_angle_precision and
line_minimum_relwidth values determine the precision of the
individual line minimizations, not the total minimization procedure,
which is governed by the stopping criteria specified in the driver's
Specify block. However, these values are important because the
precision of the line minimizations affects the the line direction
sequence orthogonality. If both are too coarse, then the selected line
directions will quickly drift away from mutual orthogonality.
Conversely, setting either too fine will
produce additional line minimization steps that do nothing to improve
convergence towards the energy minimum in the full 3N dimensional
magnetization space.
The energy_precision parameter estimates the relative
precision of the energy computations. This is used to introduce a slack
factor into the energy comparisons during the bracketing and line
minimization stages, that is, if the computed energy values at two
points have relative error difference smaller than
eprecision, they are treated as having the same energy. The
default value for eprecision is 1e-10. The true precision
will depend primarily on the number of spins in the simulation. It may
be necessary for very large simulations to increase the
eprecision value.
The method parameter can be set to either
Fletcher-Reeves or Polak-Ribiere to specify the
conjugate gradient direction selection algorithm. The default is
Fletcher-Reeves, which has somewhat smaller memory requirements.
The last parameter, fixed_spins, performs the same function
as for the Oxs_EulerEvolve class.
The Oxs_CGEvolve module provides nine scalar, one scalar
field, and two vector field outputs. The scalar outputs are
- Max mxHxm: maximum
|m x H x m|, in A/m;
m is the unit magnetization direction.
- Total energy: in joules.
- Delta E: change in energy between last step and current
step, in joules.
- Energy calc count: number of times total energy has been
calculated.
- Bracket count: total number of attempts required to
bracket energy minimum during first phase of line minimization
procedures.
- Line min count: total number of minimization steps during
second phase of line minimization procedures (i.e., steps after
minimum has been bracketed).
- Cycle count: number of line direction selections.
- Cycle sub count: number of line direction selections
since the last gradient direction reset.
- Conjugate cycle count: number of times the conjugate gradient
process has been reset to the gradient direction.
The scalar field output is
- Total energy density: cellwise total energy density, in
J/m3.
The vector field outputs are
- H: total effective field in A/m.
- mxHxm: in A/m;
m is the unit magnetization
direction.
Examples: cgtest.mif, stdprob3.mif, yoyo.mif.
Tasks are small groups of steps that can be completed without adversely
affecting user interface responsiveness. Stages are larger units
specified by the MIF problem description; in particular, problem
parameters are not expected to change in a discontinuous manner inside a
stage. The run is the complete sequence of stages, from problem start to
finish. The driver detects when stages and runs are finished, using
criteria specified in the MIF problem description, and can enforce
constraints, such as making sure stage boundaries respect time stopping
criteria.
- Oxs_TimeDriver:
- The Oxs time driver is Oxs_TimeDriver. The specify block has
the form
-
Specify Oxs_TimeDriver:name {
- evolver evolver_spec
- mesh mesh_spec
- Ms scalar_field_spec
- m0 vector_field_spec
- stopping_dm_dt torque_criteria
- stopping_time time_criteria
- stage_iteration_limit stage_iteration_count
- total_iteration_limit total_iteration_count
- stage_count number_of_stages
- stage_count_check test
- checkpoint_file restart_file_name
- checkpoint_interval checkpoint_minutes
- checkpoint_disposal cleanup_behavior
- start_iteration iteration
- start_stage stage
- start_stage_iteration stage_iteration
- start_stage_start_time stage_time
- start_stage_elapsed_time stage_elapsed_time
- start_last_timestep timestep
- normalize_aveM_output aveMflag
- report_max_spin_angle report_angle
- report_wall_time report_time
- }
The first four parameters, evolver, mesh,
Ms and m0 provide references to a time evolver, a
mesh, a scalar field and a vector field, respectively. Here Ms is
the pointwise saturation magnetization in A/m, and m0 is the
initial configuration for the magnetization unit spins, i.e.,
|m| = 1
at each point. These four parameters are required.
The next group of 3 parameters control stage stopping criteria. The
stopping_dm_dt value, in degrees per nanosecond, specifies that a
stage should be considered complete when the maximum
| dm/dt| across
all spins drops below this value. Similarly, the
stopping_time value specifies the maximum ``Simulation
time,'' i.e., the Landau-Lifshitz-Gilbert ODE (2),
(3) time, allowed per stage. For example, if
time_criteria is
1e-9, then no stage will evolve for more than
1 ns. If there were a total of 5 stages in the simulation, then the
total simulation time would be not more than 5 ns. The third way to
terminate a stage is with a stage_iteration_limit. This is
a limit on the number of successful evolver steps allowed per stage. A
stage is considered complete when any one of these three criteria are
met. Each of the criteria may be either a single value, which is
applied to every stage, or else a
grouped list
of values. If the
simulation has more stages than a criteria list has entries, then the
last criteria value is applied to all additional stages. These stopping
criteria all provide a default value of 0, meaning no constraint, but
usually at least one is specified since otherwise there is no automatic
stage termination control. For quasi-static simulations, a
stopping_dm_dt value in the range of 1.0 to 0.01 is reasonable;
the numerical precision of the energy calculations usually makes in not
possible to obtain
| dm/dt| much below 0.001 degree per nanosecond.
The total_iteration_limit, stage_count and
stage_count_check parameters involve simulation run
completion conditions. The default value for the first is 0,
interpreted as no limit, but one may limit the total number of steps
performed in a simulation by specifying a positive integer value here.
The more usual run completion condition is based on the stage count. If
a positive integer value is specified for stage_count, then the
run will be considered complete when the stage count reaches that value.
If stage_count is not specified, or is given the value 0, then the
effective number_of_stages value is computed by examining the
length of the stopping criteria lists, and also any other Oxs_Ext
object that has stage length expectations, such as
Oxs_UZeeman. The longest of these is
taken to be the stage limit value. Typically these lengths, along with
stage_count if specified, will all be the same, and any
differences indicate an error in the MIF file. Oxs will automatically
test this condition, provided stage_count_check is set to 1,
which is the default value. Stage length requests of 0 or 1 are ignored
in this test, since those lengths are commonly used to represent
sequences of arbitrary length. At times a short sequence is
intentionally specified that is meant to be implicitly extended to match
the full simulation stage length. In this case, the stage count check
can be disabled by setting test to 0.
The checkpoint
options are used to control the saving of solver state to disk; these
saves are used by the oxsii and boxsi restart feature.
The value of the checkpoint_file option is the name to
use for the solver state file. The default is
base_file_name.restart.
Cleanup of the checkpoint file is determined by the setting of
checkpoint_disposal, which should be one of
standard (the default), done_only, or never.
Under the standard setting, the checkpoint file is automatically deleted
upon normal program termination, either because the solver reached the end
of the problem, or because the user interactively terminated the problem
prematurely. If cleanup_behavior is set to
done_only, then the checkpoint file is only deleted if the
problem endpoint is reached. If cleanup_behavior is
never, then OOMMF does not delete checkpoint file; the
user is responsible for deleting this file as she desires.
The checkpoint_interval value is the time in minutes between
overwrites of the checkpoint file. No checkpoint file is written until
checkpoint_minutes have elapsed. Checkpoint writes occur
between solver iterations, so the actual interval time may be somewhat
longer than the specified time. If checkpoint_minutes is 0,
then each step is saved. Setting checkpoint_minutes to -1
disables checkpointing. The default checkpoint interval is 15 minutes.
The six start_* options control the problem run start point.
These are intended primarily for automatic use by the restart feature.
The default value for each is 0.
The normalize_aveM_output option is used to control the
scaling and units on the average magnetization components Mx, My
and Mz sent as DataTable output (this includes output sent to
mmDataTable,
mmGraph, and
mmArchive). If
aveMflag is true (1), then the output values are scaled to lie
in the range [- 1, 1], where the extreme values are obtained only at
saturation (i.e., all the spins are aligned). If aveMflag is
false (0), then the output is in A/m. The default setting is 1.
In the older MIF 2.1 format, the driver Specify block supports three
additional values: basename,
scalar_output_format, and
vector_field_output_format. In the MIF 2.2 format
these output controls have been moved into the SetOptions block.
See the SetOptions
documentation for details.
Oxs_TimeDriver provides 12 scalar outputs and 2 vector field
outputs. The scalar outputs are
- Stage: current stage number, counting from 0.
- Stage iteration: number of successful evolver steps
in the current stage.
- Iteration: number of successful evolver steps in the
current simulation.
- Simulation time: Landau-Lifshitz-Gilbert evolution
time, in seconds.
- Last time step: The size of the preceding time step, in
seconds.
- Mx/mx: magnetization component in the x direction,
averaged across the entire simulation, in A/m (Mx) or normalized units
(mx), depending on the setting of the normalize_aveM_output
option.
- My/my: magnetization component in the y direction,
averaged across the entire simulation, in A/m (My) or normalized units
(my), depending on the setting of the normalize_aveM_output
option.
- Mz/mz: magnetization component in the z direction,
averaged across the entire simulation, in A/m (Mz) or normalized units
(mz), depending on the setting of the normalize_aveM_output
option.
- Max Spin Ang: maximum angle between neighboring spins
having non-zero magnetization Ms, measured in degrees. The definition
of ``neighbor'' depends on the mesh, but for Oxs_RectangularMesh
the neighborhood of a point consists of 6 points, those nearest
forward and backward along each of the 3 coordinate axis directions.
- Stage Max Spin Ang: the largest value of ``Max Spin
Ang'' obtained across the current stage, in degrees.
- Run Max Spin Ang: the largest value of ``Max Spin
Ang'' obtained across the current run, in degrees.
- Wall time: Wall clock time, in seconds.
The three ``Max Spin Ang'' outputs are disabled by default. In general
one should refer instead to the neighboring spin angle outputs provided
by the exchange energies. However, for backward compatibility, or for
simulations without any exchange energy terms, the driver spin angle
outputs can be enabled by setting the
report_max_spin_angle option to to 1.
The ``Wall time'' output is also disabled by default. It can be enabled
by setting the report_wall_time option to to 1. It reports
the wall clock time, in seconds, since a system-dependent zero-time.
This output may be useful for performance comparisions and
debugging. (Note: The timestamp for a magnetization state is recorded
when output is first requested for that state; the timestamp is not
directly tied to the processing of the state.)
The vector field outputs are
- Magnetization: magnetization vector
M, in A/m.
- Spin: unit magnetization
m. This output ignores the
vector_field_output_format precision setting, instead
always exporting at full precision.
Examples: sample.mif, pulse.mif.
- Oxs_MinDriver:
- The Oxs driver for controlling minimization evolvers is
Oxs_MinDriver. The specify block has the form
-
Specify Oxs_MinDriver:name {
- evolver evolver_spec
- mesh mesh_spec
- Ms scalar_field_spec
- m0 vector_field_spec
- stopping_mxHxm torque_criteria
- stage_iteration_limit stage_iteration_count
- total_iteration_limit total_iteration_count
- stage_count number_of_stages
- stage_count_check test
- checkpoint_file restart_file_name
- checkpoint_interval checkpoint_minutes
- checkpoint_disposal cleanup_behavior
- start_iteration iteration
- start_stage stage
- start_stage_iteration stage_iteration
- start_stage_start_time stage_time
- start_stage_elapsed_time stage_elapsed_time
- start_last_timestep timestep
- normalize_aveM_output aveMflag
- report_max_spin_angle report_angle
- report_wall_time report_time
- }
These parameters are the same as those described for the
Oxs_TimeDriver
class, except that
stopping_mxHxm replaces stopping_dm_dt, and there is no
analogue to stopping_time. The value for stopping_mxHxm is
in A/m, and may be a
grouped list
.
Choice depends on the particulars of the simulation, but typical values
are in the range 10 to 0.1. Limits in the numerical precision of the
energy calculations usually makes it not possible to obtain
|m x H x m| below about 0.01 A/m. This control can be
disabled by setting it to 0.0.
As with Oxs_TimeDriver, in the older MIF 2.1 format this Specify
block supports three additional values: basename to control
output filenames, and output format controls
scalar_output_format and
vector_field_output_format. In the MIF 2.2 format these
output controls have been moved into the SetOptions block. See the
SetOptions
documentation for details.
Oxs_MinDriver provides 10 scalar outputs and 2 vector
field outputs. The scalar outputs are
- Stage: current stage number, counting from 0.
- Stage iteration: number of successful evolver steps
in the current stage.
- Iteration: number of successful evolver steps in the
current simulation.
- Mx/mx: magnetization component in the x direction,
averaged across the entire simulation, in A/m (Mx) or normalized units
(mx), depending on the setting of the normalize_aveM_output
option.
- My/my: magnetization component in the y direction,
averaged across the entire simulation, in A/m (My) or normalized units
(my), depending on the setting of the normalize_aveM_output
option.
- Mz/mz: magnetization component in the z direction,
averaged across the entire simulation, in A/m (Mz) or normalized units
(mz), depending on the setting of the normalize_aveM_output
option.
- Max Spin Ang: maximum angle between neighboring spins
having non-zero magnetization Ms, measured in degrees. The definition
of ``neighbor'' depends on the mesh, but for Oxs_RectangularMesh
the neighborhood of a point consists of 6 points, those nearest
forward and backward along each of the 3 coordinate axis directions.
- Stage Max Spin Ang: the largest value of ``Max Spin
Ang'' obtained across the current stage, in degrees.
- Run Max Spin Ang: the largest value of ``Max Spin
Ang'' obtained across the current run, in degrees.
- Wall time: Wall clock time, in seconds.
As is the case for the Oxs_TimeDriver, the three ``Max Spin Ang''
outputs and ``Wall time'' are disabled by default. They angle outputs
are enabled by setting the report_max_spin_angle option to
to 1, and the wall time output is enabled by setting the
report_wall_time option to to 1.
The vector field outputs are
- Magnetization: magnetization vector
M, in A/m.
- Spin: unit magnetization
m. This output ignores the
vector_field_output_format precision setting, instead
always exporting at full precision.
Examples: cgtest.mif, stdprob3.mif.
Scalar field objects are documented first. Vector field objects are
considered farther below.
- Oxs_UniformScalarField:
- Returns the same constant value regardless of the import position.
The Specify block takes one parameter, value, which is the
returned constant value. This class is frequently embedded inline to
specify homogeneous material parameters. For example, inside a driver
Specify block we may have
Specify Oxs_TimeDriver {
...
Ms { Oxs_UniformScalarField {
value 8e5
}}
...
}
As discussed in
the section on Oxs_Ext
referencing in the MIF
2 documentation,
when embedding Oxs_UniformScalarField
or Oxs_UniformVectorField
objects, a notational shorthand is allowed that lists only the value.
The previous example is exactly equivalent to
Specify Oxs_TimeDriver {
...
Ms 8e5
...
}
where an implicit Oxs_UniformScalarField object is
created with value set to 8e5.
Examples: sample.mif, cgtest.mif.
- Oxs_AtlasScalarField:
- Declares values that are defined across individual regions of an
Oxs_Atlas. The Specify block looks like
-
Specify Oxs_AtlasScalarField {
- atlas atlas_spec
- multiplier mult
- default_value scalar_field_spec
- values {
- region1_label scalar_field_spec1
- region2_label scalar_field_spec2
- ...
}
- }
The specified atlas is used to map cell locations to
regions; the value at the cell location of the scalar field from the
corresponding values sub-block is assigned to that cell.
The default_value entry is optional; if specified, and if
a cell's region is not included in the values sub-block, then
the default_value scalar field is used. If default_value
is not specified, then missing regions will raise an error.
The scalar field entries may specify any of the scalar field types
described in this (Field Objects) section. As usual, one may provide
a single numeric value in any of the scalar_field_spec
positions; this will be interpreted as requesting a uniform (spatially
homogeneous) field with the indicated value.
If the optional multiplier value is provided, then each
field value is scaled (multiplied) by the value mult.
The vector field analogue to this class is
Oxs_AtlasVectorField,
which is described below in the vector fields portion of this
section.
Examples: diskarray.mif, ellipsoid.mif,
grill.mif, spinvalve.mif, tclshapes.mif.
- Oxs_LinearScalarField:
- Returns a value that varies linearly with position. The Specify
block has the form:
-
Specify Oxs_LinearScalarField {
- norm value
- vector {
vx
vy
vz }
- offset off
- }
If optional value norm is specified, then the given
vector is first scaled to the requested size. The
offset entry is optional, with default value 0. For any
given point (x, y, z), the scalar value returned by this
object will be
xvx + yvy + zvz + off.
Example: spinvalve-af.mif.
- Oxs_RandomScalarField:
- Defines a scalar field that varies spatially in a random fashion.
The Specify block has the form:
-
Specify Oxs_RandomScalarField {
- range_min minvalue
- range_max maxvalue
- cache_grid mesh_spec
- }
The value at each position is drawn uniformly from the range declared by
the two required parameters, range_min and
range_max. There is also an optional parameter,
cache_grid, which takes a mesh specification that describes
the grid used for spatial discretization. If
cache_grid is not specified, then each call to
Oxs_RandomScalarField generates a different field. If you want to
use the same random scalar field in two places (as a base for setting,
say anisotropy coefficients and saturation magnetization), then specify
cache_grid with the appropriate (usually the base problem)
mesh.
Examples: randomshape.mif, stdprob1.mif.
- Oxs_ScriptScalarField:
- Analogous to the parallel
Oxs_ScriptVectorField
class, this class produces a scalar field dependent on a Tcl script
and optionally other scalar and vector fields. The Specify block has
the form
-
Specify Oxs_ScriptScalarField:name {
- script Tcl_script
- script_args { args_request }
- scalar_fields { scalar_field_spec ...}
- vector_fields { vector_field_spec ...}
- atlas atlas_spec
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- }
For each point of interest, the specified script is
called with the arguments requested by script_args
appended to the command, as explained in the User
Defined Support Procedures section of the MIF 2 file
format documentation. The value for script_args should be a
subset of {rawpt relpt minpt maxpt span scalars vectors }.
If rawpt is requested, then when the Tcl proc is called, at
the corresponding spot in the argument list the x, y,
z values of point will be placed, in problem coordinates (in
meters). The points so passed will usually be node points in the
simulation discretization (the mesh), but
this does not have to be the case in general. The relpt,
minpt, maxpt, and span rely on a definition of a
bounding box, which is an axes parallel parallelepiped. The
bounding box must be specified by either referencing an
atlas, or by explicitly stating the range via the three
entries xrange, yrange, zrange (in
meters). The minpt and maxpt arguments list the minimum
and maximum values of the bounding box (coordinate by coordinate),
while span provides the 3-vector resulting from
(maxpt - minpt). The relpt selection provides x_rel,
y_rel, z_rel, where each element lies in the range
[0, 1], indicating a relative position between minpt and
maxpt, coordinate-wise.
Each of the script_args discussed so far places exactly 3
arguments onto the Tcl proc argument list. The last two,
scalars and vectors, place arguments depending on the size
of the scalar_fields and vector_fields lists.
The scalar_fields value is a list of other scalar field
objects. Each scalar field is evaluated at the point in question,
and the resulting scalar value is placed on the Tcl proc argument
list, in order. The vector_fields option works similarly,
except each vector field generates three points for the Tcl proc
argument list, since the output from vector field objects is a three
vector. Although the use of these entries appears complicated, this
is a quite powerful facility that allows nearly unlimited control for
the modification and combination of other field objects. Both
scalar_fields and vector_fields entries are optional.
If script_args is not specified, the default value relpt
is used.
Note that if script_args includes relpt, minpt,
maxpt, or span, then a bounding box must be specified, as
discussed above. The following example uses the explicit range
method. See the Oxs_ScriptVectorField
documentation
for an example using an atlas specification.
proc Ellipsoid { xrel yrel zrel } {
set xrad [expr {$xrel - 0.5}]
set yrad [expr {$yrel - 0.5}]
set zrad [expr {$zrel - 0.5}]
set test [expr {$xrad*$xrad+$yrad*$yrad+$zrad*$zrad}]
if {$test>0.25} {return 0}
return 8.6e5
}
Specify Oxs_ScriptScalarField {
script Ellipsoid
xrange { 0 1e-6 }
yrange { 0 250e-9 }
zrange { 0 50e-9 }
}
This Oxs_ScriptScalarField object returns 8.6e5 if the import (x,y,z) lies within the ellipsoid
inscribed inside the axes parallel parallelepiped defined by (xmin=0,
ymin=0, zmin=0) and (xmax=1e-6, ymax=250e-9, zmax=50e-9), and 0
otherwise.
See also the discussion of the
ReadFile MIF extension command
for an example using
an imported image file for similar purposes.
Below is one more example, illustrating the use of the
vector_fields option.
proc DotProduct { x1 y1 z1 x2 y2 z2 } {
return [expr {$x1*$x2+$y1*$y2+$z1*$z2}]
}
Specify Oxs_FileVectorField:file1 {
atlas :atlas
file file1.omf
}
Specify Oxs_UniformVectorField:dir111 {
norm 1
vector {1 1 1}
}
Specify Oxs_ScriptScalarField:project {
script DotProduct
script_args vectors
vector_fields {:file1 :dir111}
}
The scalar field :project yields at each point in space the
projection of the vector field :file1 onto the [1,1,1] direction.
Examples: antidots-filled.mif,
ellipsoid-fieldproc.mif, manyregions-scriptfields.mif,
manyspheres.mif, varalpha.mif.
- Oxs_VecMagScalarField:
- The Oxs_VecMagScalarField class produces a scalar field
from a vector field by taking the norm of the vector field on a
point-by-point basis, i.e.,
|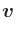 | =
| = 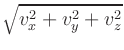 .
.
The Specify block has the form:
-
Specify Oxs_VecMagScalarField {
- field vector_field_spec
- multiplier mult
- offset off
- }
The multiplier and offset entries are applied
after the vector norm, i.e., the resulting scalar field is
mult * |v| + off. The default values
for mult and off are 1 and 0, respectively.
The functionality of the Oxs_VecMagScalarField class may be achieved
with the Oxs_ScriptScalarField class by using the
vector_fields option and a Tcl script to compute the vector
norm. However, this particular functionality is needed frequently
enough that a specialized class is useful. For example, this class can
be used in conjunction with a vector field object to set
both the saturation magnetization distribution (Ms) and the initial
magnetization:
Specify Oxs_FileVectorField:file1 {
atlas :atlas
file file1.omf
}
Specify Oxs_TimeDriver {
basename test
evolver :evolve
stopping_dm_dt 0.01
mesh :mesh
m0 :file1
Ms { Oxs_VecMagScalarField {
field :file1
}}
}
Example: sample-vecrotate.mif.
- Oxs_ScriptOrientScalarField:
- Scalar fields provide scalar values as a function of position across
three-space. The Oxs_ScriptOrientScalarField class is used to
compose a transformation on the input position before evaluation by
a scalar field. The Specify block has the form:
-
Specify Oxs_ScriptOrientScalarField:name {
- field scalar_field_spec
- script Tcl_script
- script_args { args_request }
- atlas atlas_spec
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- }
The field argument should refer to a scalar field object.
The script is a Tcl script that should return a position
vector that will be sent on the field object to ultimately
produce a scalar value. The arguments to the Tcl_script are
determined by script_args, which should be a subset of
{relpt rawpt minpt maxpt span }. If any arguments other than
rawpt are requested, then the bounding box must be specified by
either the atlas option, or else through the three xrange,
yrange, zrange entries. The default value for
script_args is relpt.
The Oxs_ScriptOrientScalarField class can be used to change the
``orientation'' of a scalar field, as in the following simple example,
which reflects the :file1mag scalar field across the yz-plane:
Specify Oxs_FileVectorField:file1 {
atlas :atlas
file file1.omf
}
Specify Oxs_VecMagScalarField:file1mag {
field :file1
}
proc Reflect { x y z xmin ymin zmin xmax ymax zmax} {
return [list [expr {($xmax+$xmin-$x)}] $y $z]
}
Specify Oxs_ScriptOrientScalarField:reflect {
field :file1mag
script Reflect
script_args {rawpt minpt maxpt}
atlas :atlas
}
See also the
Oxs_ScriptOrientVectorField
class for
analogous operations on vector fields.
Example: sample-reflect.mif.
- Oxs_AffineOrientScalarField:
- The Oxs_AffineOrientScalarField class is similar to the
Oxs_ScriptOrientScalarField class, except that the transformation
on the import position is by an affine transformation defined in terms
of a 3x3 matrix and an offset instead of a
Tcl script. Although this functionality can be obtained by an
appropriate Tcl script, the Oxs_AffineOrientScalarField is
easier to use and will run faster, as the underlying transformation is
performed by compiled C++ instead of Tcl script.
The Specify block has the form:
-
Specify Oxs_AffineOrientScalarField {
- field scalar_field_spec
- M
{ matrix_entries ... }
- offset {
offx
offy
offz }
- inverse invert_flag
- inverse_slack slack
- }
If
F(x) represents the scalar field specified by the
field value, then the resulting transformed scalar field is
F(Mx + off). Here M is a
3x3 matrix, which may be specified by a list
of 1, 3, 6 or 9 entries. If the matrix_entries list consists of a
single value, then M is taken to be that value times the identity
matrix, i.e., M is a homogeneous scaling transformation. If
matrix_entries consists of 3 values, then M is taken to be the
diagonal matrix with those three values along the diagonal.
If matrix_entries is 6 elements long, then M is assumed to be a
symmetric matrix, where the 6 elements specified correspond to M11,
M12, M13, M22, M23, and M33. Finally, if
matrix_entries is 9 elements long, then the elements specify the
entire matrix, in the order M11, M12, M13, M21,
..., M33. If M is not specified, then it is taken to be
the identity matrix.
The offset entry is simply a 3-vector that is added to
Mx. If offset is not specified, then
it is set to the zero vector.
It is frequently the case that the transformation that one wants to
apply is not
Mx + off, but rather the
inverse, i.e.,
M-1(x - off). Provided M
is nonsingular, this can be accomplished by setting the
inverse option to 1. In this case the matrix M.M-1 is
compared to the identity matrix, to check the accuracy of the matrix
inversion. If any entry in M.M-1 differs from I by more than the
8-byte float machine precision (typically
2e-16) times the value of
inverse_slack, then an error is raised. The default setting
for invert_flag is 0, meaning don't invert,
and the default setting for slack is 128.
Here is an example using Oxs_AffineOrientScalarField to rotate a
field by 90 degrees counterclockwise about the
z-axis. Note that the specified atlas is square in x and y, with
the origin of the atlas coordinates in the center of the atlas volume.
Specify Oxs_BoxAtlas:atlas {
xrange {-250e-9 250e-9}
yrange {-250e-9 250e-9}
zrange { -15e-9 15e-9}
}
Specify Oxs_FileVectorField:file1 {
atlas :atlas
file file1.omf
}
Specify Oxs_VecMagScalarField:file1mag {
field :file1
}
Specify Oxs_AffineOrientScalarField:reflect {
field :file1mag
M { 0 1 0
-1 0 0
0 0 1 }
}
See also the
Oxs_AffineOrientVectorField
class for
analogous operations on vector fields.
Example: sample-rotate.mif.
- Oxs_AffineTransformScalarField:
- Like the Oxs_AffineOrientScalarField class, this class composes
an affine transform with a separate scalar field, but in this case the
affine transform is applied after the field evaluation.
The Specify block has the form:
-
Specify Oxs_AffineTransformScalarField {
- field scalar_field_spec
- multiplier mult
- offset off
- inverse invert_flag
- }
If
F(x) represents the scalar field specified by the
field value, then the resulting scalar field is
mult*F(x) + off. Since the output
from F is a scalar, both multiplier and offset
are scalars. If inverse is 1, then the transform is changed
to
 F(x) - off
F(x) - off /mult,
provided mult is non-zero.
/mult,
provided mult is non-zero.
The default values for mult, off, and
invert_flag are 1, 0, and 0, respectively. The field
value is the only required entry.
The functionality provided by Oxs_AffineTransformScalarField can
also be produced by the
Oxs_ScriptScalarField
class with the
scalar_fields entry, but the Oxs_AffineTransformScalarField
class is faster and has a simpler interface. See also the
Oxs_AffineTransformVectorField
class for analogous
operations on vector fields.
Example: sample-rotate.mif.
- Oxs_ImageScalarField:
- This class creates a scalar field using an image. The Specify block has
the form
-
Specify Oxs_ImageScalarField:name {
- image pic
- invert invert_flag
- multiplier mult
- offset off
- viewplane view
- atlas atlas_spec
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- exterior ext_flag
- }
The image is interpreted as a monochromatic map, yielding a
scalar field with black corresponding to zero and white to one if
invert is 0 (the default), or with black corresponding to 1
and white to 0 if invert is 1. Color images are converted to
grayscale by simply summing the red, green, and blue components. A
multiplier option is available to change the range of values
from [0, 1] to
[0,mult], after which the
offset value, if any, is added.
The viewplane is treated in the same manner as the viewplane
option in the Oxs_ImageAtlas class, and should
likewise take one of the three two-letter codes xy (default),
zx or yz. The spatial scale is adjusted to fit the volume
specified by either the atlas or
xrange/yrange/zrange selections. If the specified volume
does not fill the entire simulation volume, then points outside the
specified volume are handled as determined by the exterior
setting, which should be either a floating point value, or one of the
keywords boundary or error. In the first case, the floating
point value is treated as a default value for points outside the image,
and should have a value in the range [0, 1]. The multiplier and offset
adjustments are made to this value in the same way as to points inside
the image. If ext_flag is boundary, then points outside the
image are filled with the value of the closest point on the boundary of
the image. If ext is error (the default), then an error
is raised if a value is needed for any point outside the image.
Examples: rotatecenterstage.mif, sample-reflect.mif.
- Oxs_UniformVectorField:
- Returns the same constant value regardless of the import position.
The Specify block takes one required parameter, vector,
which is a 3-element list of the vector to return, and one optional
parameter, norm, which if specified adjusts the size of
export vector to the specified magnitude. For example,
-
Specify Oxs_UniformVectorField {
- norm 1
- vector {1 1 1}
- }
This object returns the unit vector (a, a, a), where
a=1/sqrt(3), regardless of the import
position.
This class is frequently embedded inline to specify spatially uniform
quantities. For example, inside a driver Specify block we may have
Specify Oxs_TimeDriver {
...
m0 { Oxs_UniformVectorField {
vector {1 0 0}
}}
...
}
As discussed in
the section on Oxs_Ext
referencing in the MIF
2 documentation,
when embedding Oxs_UniformVectorField
or Oxs_UniformScalarField
objects, a notational shorthand is allowed that lists only the required
value. The previous example is exactly equivalent to
Specify Oxs_TimeDriver {
...
m0 {1 0 0}
...
}
where an implicit Oxs_UniformVectorField object is
created with the value of vector set to {1 0 0 }.
Examples: sample.mif, cgtest.mif.
- Oxs_AtlasVectorField:
- Declares vector values that are defined across individual regions of
an Oxs_Atlas. The Specify block has the form
-
Specify Oxs_AtlasVectorField {
- atlas atlas_spec
- norm magval
- multiplier mult
- default_value vector_field_spec
- values {
- region1_label vector_field_spec1
- region2_label vector_field_spec2
- ...
}
- }
Interpretation is analogous to the
Oxs_AtlasScalarField
specify block, except here the output values are 3 dimensional
vectors rather than scalars. Thus the values associated with each
region are vector fields rather than scalar fields. Any of the
vector field types described in this (Field Objects) section may be
used. As usual, one may provided a braced list of three numeric
values to request a uniform (spatially homogeneous) vector field with
the indicated value.
The optional norm parameter causes each vector value to be
scaled to have magnitude magval. The optional
multiplier value scales the field values. If both
norm and multiplier are specified, then the field vectors
are first normalized before being scaled by the multiplier value.
Examples: diskarray.mif, exchspring.mif,
imageatlas.mif, spinvalve.mif.
- Oxs_ScriptVectorField:
- Conceptually similar to the
Oxs_ScriptScalarField scalar
field object,
except that the script should return a vector (as a 3 element list)
rather than a scalar. In addition to the parameters accepted by
Oxs_ScriptScalarField, Oxs_ScriptVectorField also accepts
an optional parameter norm. If specified, the return
values from the script are size adjusted to the specified magnitude.
If both norm and multiplier are specified, then
the field vectors are first normalized before being scaled by the
multiplier value.
The following example produces a vortex-like unit vector field, with
an interior core region pointing parallel to the z-axis. Here the
scaling region is specified using an atlas reference to an
object named ``:atlas'', which is presumed to be defined earlier in
the MIF file. See the Oxs_ScriptScalarField sample Specify
block for an example using the explicit range option.
proc Vortex { xrel yrel zrel } {
set xrad [expr {$xrel-0.5}]
set yrad [expr {$yrel-0.5}]
set normsq [expr {$xrad*$xrad+$yrad*$yrad}]
if {$normsq <= 0.025} {return "0 0 1"}
return [list [expr {-1*$yrad}] $xrad 0]
}
Specify Oxs_ScriptVectorField {
script Vortex
norm 1
atlas :atlas
}
See also the
Oxs_MaskVectorField
documentation and the discussion of the
ReadFile MIF extension command
for other example uses of the Oxs_ScriptVectorField class.
Examples: cgtest.mif, ellipsoid.mif,
manyregions-scriptfields.mif, sample-vecreflect.mif,
stdprob3.mif, yoyo.mif.
- Oxs_FileVectorField:
- Provides a file-specified vector field. The Specify block has the form
-
Specify Oxs_FileVectorField {
- file filename
- atlas atlas_spec
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- spatial_scaling {
xscale yscale zscale
}
- spatial_offset {
xoff yoff zoff
}
- exterior ext_flag
- norm magnitude
- multiplier mult
- }
Required values in the Specify block are the name of the input vector
field file and the desired scaling parameters. The filename is
specified via the file entry, which names a file
containing a vector field in one of the formats recognized by
avf2ovf. If
atlas or xrange/yrange/zrange are specified,
then the file will be scaled and translated as necessary to fit that
scaling region, in the same manner as done, for example, by
the Oxs_ScriptScalarField and
Oxs_ScriptVectorField classes.
Alternatively, one may specify spatial_scaling and
spatial_offset directly. In this case the vector spatial
positions are taken as specified in the file, multiplied
component-wise by (xscale,yscale,zscale), and then translated by
(xoff,yoff,zoff). If you want to use the spatial coordinates as
directly specified in the file, use (1,1,1) for spatial_scaling
and (0,0,0) for spatial_offset.
In all cases, once the input field has been scaled and translated, it
is then sub-sampled (zeroth-order fit) as necessary to match the
simulation mesh.
The exterior flag determines the behavior at ``exterior
points'', i.e., locations (if any) in the simulation mesh that lie
outside the extent of the scaled and translated vector field. The
ext_flag should be either a three-vector, or one of the
keywords boundary or error. If a three-vector is given,
then that value is supplied at all exterior points. If
ext_flag is set to boundary, then the value used is
the point on the boundary of the input vector field that is closest
to the exterior point. The default setting for ext_flag is
error, which raises an error if there are any exterior points.
The magnitude of the field can be modified by the optional
norm and multiplier attributes. If the norm
parameter is given, then each vector in the field will be
renormalized to the specified magnitude. If the multiplier parameter
is given, then each vector in the field will be multiplied by the
given scalar value. If the multiplier value is negative, the field
direction will be reversed. If both norm and multiplier
are given, then the field vectors are renormalized before being
scaled by the multiplier value.
Examples: stdprob3.mif, yoyo.mif.
- Oxs_RandomVectorField:
- Similar to
Oxs_RandomScalarField, but defines a vector field rather than a scalar field that
varies spatially in a random fashion. The Specify block has the form:
-
Specify Oxs_RandomVectorField {
- min_norm minvalue
- max_norm maxvalue
- cache_grid mesh_spec
- }
The Specify block takes two required parameters, min_norm
and max_norm. The vectors produced will have magnitude
between these two specified values. If min_norm = max_norm,
then the samples are uniformly distributed on the sphere of that radius.
Otherwise, the samples are uniformly distributed in the hollow spherical
volume with inner radius min_norm and outer radius max_norm.
There is also an optional parameter, cache_grid, which takes
a mesh specification that describes the grid used for cache spatial
discretization. If cache_grid is not specified, then each
call to Oxs_RandomVectorField generates a different field. If you
want to use the same random vector field in two places (as a base for
setting, say anisotropy axes and initial magnetization), then specify
cache_grid with the appropriate (usually the base problem)
mesh.
Examples: diskarray.mif, sample2.mif,
randomshape.mif stdprob1.mif.
- Oxs_PlaneRandomVectorField:
- Similar to Oxs_RandomVectorField, except that samples are
drawn from 2D planes rather than 3-space. The Specify block has the
form
-
Specify Oxs_RandomVectorField {
- plane_normal vector_field_spec
- min_norm minvalue
- max_norm maxvalue
- cache_grid mesh_spec
- }
The min_norm, max_norm, and
cache_grid parameters have the same meaning as for the
Oxs_RandomVectorField class. The additional parameter,
plane_normal, specifies a vector field that at each point
provides a vector that is orthogonal to the plane from which the
random vector at that point is to be drawn. If the vector field is
specified explicitly as three real values, then a spatially uniform
vector field is produced and all the random vectors will lie in the
same plane. More generally, however, the normal vectors (and
associated planes) may vary from point to point. As a special case,
if a normal vector at a point is the zero vector, then no planar
restriction is made and the resulting random vector is drawn uniformly
from a hollow ball in three space satisfying the minimum/maximum norm
constraints.
Example: sample2.mif.
- Oxs_ScriptOrientVectorField:
- This class is analogous to the
Oxs_ScriptOrientScalarField
class.
The Specify block has the form:
-
Specify Oxs_ScriptOrientVectorField:name {
- field vector_field_spec
- script Tcl_script
- script_args { args_request }
- atlas atlas_spec
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- }
The interpretation of the specify block and the operation of the Tcl script is exactly the same as for the Oxs_ScriptOrientScalarField
class, except the input field and the resulting field are
vector fields instead of scalar fields.
Note that the ``orientation'' transformation is applied to the import
spatial coordinates only, not the output vector. For example, if the
field value represents a shaped vector field, and the script
proc is a rotation transformation, then the resulting vector field shape
will be rotated as compared to the original vector field, but the output
vectors themselves will still point in their original directions. In such
cases one may wish to compose the Oxs_ScriptOrientVectorField with
a Oxs_ScriptVectorField
object to rotate the
output vectors as well. This situation occurs also with the
Oxs_AffineOrientVectorField class. See the
Oxs_AffineTransformVectorField
class documentation for an
example illustrating the composition of an object of that class with a
Oxs_AffineOrientVectorField
object.
Example: sample-vecreflect.mif.
- Oxs_AffineOrientVectorField:
- This class is analogous to the
Oxs_AffineOrientScalarField
class.
The Specify block has the form:
-
Specify Oxs_AffineOrientVectorField {
- field vector_field_spec
- M
{ matrix_entries ... }
- offset {
offx
offy
offz }
- inverse invert_flag
- inverse_slack slack
- }
The interpretation of the specify block and the affine transformation
is exactly the same as for the Oxs_AffineOrientScalarField
class, except the input field and the resulting field are
vector fields instead of scalar fields.
As explained in the
Oxs_ScriptOrientVectorField
documentation, the ``orientation'' transformation is applied to the
import spatial coordinates only, not the output vector. If one wishes
to rotate the output vectors, then a
Oxs_AffineTransformVectorField
object may be applied with the opposite rotation. See that section for
an example.
Examples: yoyo.mif, sample-vecrotate.mif.
- Oxs_AffineTransformVectorField:
- This class applies an affine transform to the output of a vector field.
It is similar to the
Oxs_AffineTransformScalarField
class, except
that in this case the affine transform is applied to a vector instead of
a scalar. The Specify block has the form:
-
Specify Oxs_AffineTransformVectorField {
- field vector_field_spec
- M
{ matrix_entries ... }
- offset {
offx
offy
offz }
- inverse invert_flag
- inverse_slack slack
- }
Because the output from field is a 3-vector, the transform
defined by M and offset requires M to be a
3x3 matrix and offset to be a 3-vector.
Thus, if
v(x) represents the
vector field specified by the field value, then the resulting
vector field is
M.v(x) + off.
M is described by a list of from one to nine entries, in exactly
the same manner as for the
Oxs_AffineOrientVectorField
and
Oxs_AffineOrientScalarField
classes. The
interpretation of offset, inverse, and
inverse_slack is also the same. In particular, if
invert_flag is 1, then the resulting vector field is
M-1. v(x) - off
v(x) - off .
.
The following example illustrates combining a
Oxs_AffineTransformVectorField with a
Oxs_AffineOrientVectorField
to completely rotate a vector field.
Specify Oxs_BoxAtlas:atlas {
xrange {-80e-9 80e-9}
yrange {-80e-9 80e-9}
zrange {0 40e-9}
}
proc Trap { x y z } {
if {$y<=$x && $y<=0.5} {return [list 0 1 0]}
return [list 0 0 0]
}
Specify Oxs_ScriptVectorField:trap {
script Trap
atlas :atlas
}
Specify Oxs_AffineOrientVectorField:orient {
field :trap
M { 0 -1 0
1 0 0
0 0 1 }
offset { -20e-9 0 0 }
inverse 1
}
Specify Oxs_AffineTransformVectorField:rot {
field :orient
M { 0 -1 0
1 0 0
0 0 1 }
}
proc Threshold { vx vy vz } {
set magsq [expr {$vx*$vx+$vy*$vy+$vz*$vz}]
if {$magsq>0} {return 8e5}
return 0.0
}
Specify Oxs_ScriptScalarField:Ms {
vector_fields :rot
script Threshold
script_args vectors
}
Specify Oxs_TimeDriver {
m0 :rot
Ms :Ms
stopping_dm_dt 0.01
evolver :evolve
mesh :mesh
}
The base field here is given by the Oxs_ScriptVectorField:trap
object, which produces a vector field having a trapezoidal shape with
the non-zero vectors pointing parallel to the y-axis. The
:orient and :rot transformations rotate the shape and the
vectors counterclockwise 90 degrees.
Additionally, the offset option in :orient translates the
shape 20 nm towards the left. The original and transformed fields are
illustrated below.
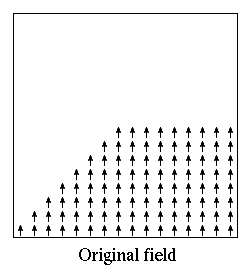
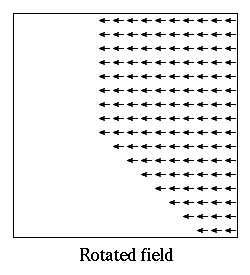
Example: sample-vecrotate.mif.
- Oxs_MaskVectorField:
- Multiplies a vector field pointwise by a scalar vector field (the mask)
to produce a new vector field. The Specify block has the form:
-
Specify Oxs_MaskVectorField {
- mask scalar_field_spec
- field vector_field_spec
- }
This functionality can be achieved, if in a somewhat more complicated
fashion, with the
Oxs_ScriptVectorField
class. For example, given a scalar field :mask and a vector field
:vfield, this example using the Oxs_MaskVectorField class
Specify Oxs_MaskVectorField {
mask :mask
field :vfield
}
is equivalent to this example using the Oxs_ScriptVectorField
class
proc MaskField { m vx vy vz } {
return [list [expr {$m*$vx}] [expr {$m*$vy}] [expr {$m*$vz}]]
}
Specify Oxs_ScriptVectorField {
script MaskField
script_args {scalars vectors}
scalar_fields { :mask }
vector_fields { :vfield }
}
Of course, the Oxs_ScriptVectorField approach is easily
generalized to much more complicated and arbitrary combinations of
scalar and vector fields.
Example: rotatecenterstage.mif.
- Oxs_ImageVectorField:
- This class creates a vector field using an image. The Specify block has
the form
-
Specify Oxs_ImageVectorField:name {
- image pic
- multiplier mult
- vx_multiplier xmult
- vy_multiplier ymult
- vz_multiplier zmult
- vx_offset xoff
- vy_offset yoff
- vz_offset zoff
- norm norm_magnitude
- viewplane view
- atlas atlas_spec
- xrange { xmin xmax }
- yrange { ymin ymax }
- zrange { zmin zmax }
- exterior ext_flag
- }
The image is interpreted as a three-color map, yielding a
vector field where each (x,y,z) component is determined by the red,
green, and blue color components, respectively....
The viewplane, atlas,
xrange/yrange/zrange, and exterior are treated
the same as for the
Oxs_ImageScalarField class
Examples: NONE.
Refer to the MIF 2 documentation for details on the base format
specification.
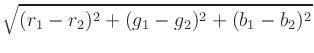 .
.
![]() , then all colors will match, and no pixels will be
assigned to the default region. If matcherror is not specified,
then the default value for max_color_distance is 3, which
means all colors match.
, then all colors will match, and no pixels will be
assigned to the default region. If matcherror is not specified,
then the default value for max_color_distance is 3, which
means all colors match.

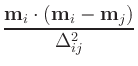
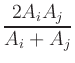 ,
,
![$\displaystyle {\frac{{\sigma\left[1-\textbf{m}_i\cdot\textbf{m}_j\right]
+\sig...
...\left[1-\left(\textbf{m}_i\cdot\textbf{m}_j\right)^2\right]
}}{{\Delta_{ij}}}}$](img17.gif)
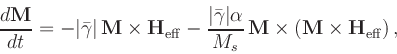
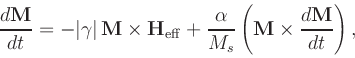
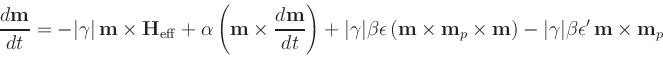
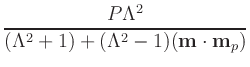
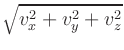 .
.

