Press
here
to get the full document in PostScript format.
Press
here
to get this subdocument in PostScript format.
Numerical Evaluation of Special Functions
D. W. Lozier and F. W. J. Olver
5.7. Incomplete Gamma Functions, Generalized Exponential Integrals
.
These functions are essentially equivalent; thus
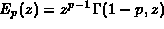 .
This section includes the chi-square distribution function.
.
This section includes the chi-square distribution function.
5.7.1. Real z and Integer or Half-Integer p.
Software Packages:
[ Amo80a, Fortran]
,
[ SP75, Fortran]
,
[ SZ74, Fortran]
.
Intermediate Libraries:
[ Mos89]
,
[ ULI90]
.
Comprehensive Libraries:
SLATEC.
Interactive Systems:
Maple.
5.7.2. Real z and Real p.
Software Packages:
[ CLM90a, Fortran]
,
[ CLM90b, Fortran]
,
[ DM87, Fortran]
,
[ Ful72, Fortran]
,
[ Gau79a, Fortran]
,
[ Moo82, Fortran]
,
[ She88, Fortran]
,
[ Tem94, Pascal]
.
Intermediate Libraries:
[ Bak92]
,
[ Mos89]
,
[ ULI90]
.
Comprehensive Libraries:
IMSL,
NAG,
Numerical Recipes,
Scientific Desk,
SLATEC.
5.7.3. Complex z and Real or Complex p.
Interactive Systems:
Maple,
Mathematica.
5.7.4. Inverse Function.
Software Packages:
[ DM87, Fortran]
,
[ Phi88, Fortran]
.
Intermediate Libraries:
[ Mos89]
,
[ ULI90]
.
Comprehensive Libraries:
IMSL,
NAG,
Scientific Desk.
Interactive Systems:
Maple,
Mathematica.
5.7.5. Articles.
[ AB87a]
,
[ Amo80b]
,
[ Bar61]
,
[ CLM87]
,
[ CLM88]
,
[ CLM90c]
,
[ DM86]
,
[ Gau79b]
,
[ JT85]
,
[ LDP93]
,
[ Luk75]
,
[ Mar82]
,
[ Tem85]
,
[ Tem87]
,
[ Tem92a]
.
References
- AB87
-
G. Allasia and R. Besenghi, Numerical calculation of incomplete gamma
functions by the trapezoidal rule, Numer. Math. 50 (1987), 419--428.
- Amo80a
-
D. E. Amos, Algorithm 556. Exponential integrals, ACM Trans. Math.
Software 6 (1980), 420--428, for remark see same journal v. 9 (1983),
p. 525.
- Amo80b
-
D. E. Amos, Computation of exponential integrals, ACM Trans. Math.
Software 6 (1980), 365--377.
- Bak92
-
L. Baker, C mathematical function handbook, McGraw-Hill, Inc., New
York, 1992, includes diskette.
- Bar61
-
R. Barakat, Evaluation of the incomplete gamma function of imaginary
argument by Chebyshev polynomials, Math. Comp. 15 (1961), 7--11.
- CLM87
-
C. Chiccoli, S. Lorenzutta, and G. Maino, A numerical method for
generalized exponential integrals, Comput. Math. Appl. 14 (1987),
261--268.
- CLM88
-
C. Chiccoli, S. Lorenzutta, and G. Maino, On the evaluation of generalized
exponential integrals
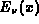 , J. Comput. Phys. 78 (1988),
278--287.
, J. Comput. Phys. 78 (1988),
278--287.
- CLM90a
-
C. Chiccoli, S. Lorenzutta, and G. Maino, An algorithm for exponential
integrals of real order, Computing 45 (1990), 269--276.
- CLM90b
-
C. Chiccoli, S. Lorenzutta, and G. Maino, Calculation of exponential
integrals of real order, Internat. J. Comput. Math. 31 (1990),
125--135.
- CLM90c
-
C. Chiccoli, S. Lorenzutta, and G. Maino, On a Tricomi series
representation for the generalized exponential integral, Internat. J.
Comput. Math. 31 (1990), 257--262.
- DM86
-
A. R. DiDonato and A. H. Morris, Jr., Computation of the incomplete
gamma function ratios and their inverse, ACM Trans. Math. Software 12
(1986), 377--393.
- DM87
-
A. R. DiDonato and A. H. Morris, Jr., Algorithm 654. Fortran
subroutines for computing the incomplete gamma function ratios and their
inverse, ACM Trans. Math. Software 13 (1987), 318--319.
- Ful72
-
L. W. Fullerton, Algorithm 435. Modified incomplete gamma function,
Comm. ACM 15 (1972), 993--995, for remark see ACM Trans. Math. Software
v. 4 (1978), pp. 296--304.
- Gau79a
-
W. Gautschi, Algorithm 542. Incomplete gamma functions, ACM Trans.
Math. Software 5 (1979), 482--489.
- Gau79b
-
W. Gautschi, A computational procedure for incomplete gamma functions,
ACM Trans. Math. Software 5 (1979), 466--481.
- JT85
-
W. B. Jones and W. J. Thron, On the computation of incomplete gamma
functions in the complex domain, J. Comput. Appl. Math. 12/13 (1985),
401--417.
- LDP93
-
Y. Li, X. Dong, and S. Pan, Computation of auxiliary functions in STO
molecular integrals up to arbitrary accuracy. I. Evaluation of incomplete
gamma function
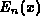 by forward recursion, Internat. J. Quantum Chem.
45 (1993), 3--14.
by forward recursion, Internat. J. Quantum Chem.
45 (1993), 3--14.
- Luk75
-
Y. L. Luke, Mathematical functions and their approximations, Academic
Press, New York, 1975.
- Mar82
-
A. L. Marshak, On the approximation of the exponential integral by
quadrature formulae, U.S.S.R. Comput. Math. and Math. Phys. 22 (1982),
no. 5, 20--28.
- Moo82
-
R. J. Moore, Algorithm AS 187. Derivatives of the incomplete gamma
integral, Appl. Statist. 31 (1982), 330--335.
- Mos89
-
S. L. B. Moshier, Methods and programs for mathematical functions, Ellis
Horwood Limited, Chichester, 1989, separate diskette.
- Phi88
-
H. N. Phien, A Fortran routine for the computation of gamma
percentiles, Adv. Engrg. Software 10 (1988), 159--164.
- She88
-
B. L. Shea, Algorithm AS 239. Chi-squared and incomplete gamma
integral, Appl. Statist. 37 (1988), 466--473.
- SP75
-
P. Spellucci and P. Pulay, Effective calculation of the incomplete gamma
function for parameter values
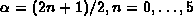 , Angew.
Informatik 17 (1975), 30--32.
, Angew.
Informatik 17 (1975), 30--32.
- SZ74
-
I. A. Stegun and R. Zucker, Automatic computing methods for special
functions. Part II. The exponential integral
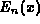 , J. Res. Nat.
Bur. Standards 78B (1974), 199--216.
, J. Res. Nat.
Bur. Standards 78B (1974), 199--216.
- Tem85
-
N. M. Temme, Special functions as approximants in uniform asymptotic
expansions of integrals ; A survey, Rend. Sem. Mat. Univ. Politec.
Torino Fascicolo Speciale. Special Functions: Theory and Computation
(1985), 289--317.
- Tem87
-
N. M. Temme, On the computation of the incomplete gamma functions for
large values of the parameters, Inst. Math. Appl. Conf. Ser. New Ser., vol.
10: Algorithms for Approximation (Shrivenham, 1985), Oxford Univ. Press,
New York, 1987, pp. 479--489.
- Tem92
-
N. M. Temme, Asymptotic inversion of incomplete gamma functions, Math.
Comp. 58 (1992), 755--764.
- Tem94
-
N. M. Temme, A set of algorithms for the incomplete gamma functions,
Probab. Engrg. Inform. Sci. (1994), in press.
- ULI90
-
Mathematical function library for Microsoft--C, United Laboratories,
Inc., John Wiley & Sons, 1990, includes diskettes. Edition also
exists in Fortran (1989).
Abstract:
This document is an excerpt from the current hypertext version of
an article that appeared in Walter Gautschi (ed.),
Mathematics of Computation 1943--1993: A Half-Century of
Computational Mathematics, Proceedings of Symposia in
Applied Mathematics 48, American Mathematical Society,
Providence, RI 02940, 1994.
The symposium was held at the University of British Columbia
August 9--13, 1993, in honor of the fiftieth anniversary of
the journal Mathematics of Computation.
The original abstract follows.
Higher transcendental functions continue to play varied and
important roles in investigations by engineers, mathematicians,
scientists and statisticians.
The purpose of this paper is to assist in locating useful approximations
and software for the numerical generation of these functions, and to
offer some suggestions for future developments in this field.
Applied and Computational Mathematics Division,
National Institute of Standards and Technology,
Gaithersburg, Md 20899
E-mail address: [email protected]
Institute for Physical Science and Technology,
University of Maryland,
College Park, MD 20742
E-mail address: [email protected]
The research of the second author has been supported by NSF
Grant CCR 89-14933.
1991 Mathematics Subject Classification. Primary 65D20;
Secondary 33-00.
Daniel W Lozier
Fri Apr 7 14:16:08 EDT 1995
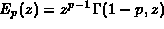 .
This section includes the chi-square distribution function.
.
This section includes the chi-square distribution function.
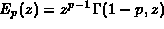 .
This section includes the chi-square distribution function.
.
This section includes the chi-square distribution function.
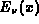 , J. Comput. Phys. 78 (1988),
278--287.
, J. Comput. Phys. 78 (1988),
278--287.
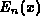 by forward recursion, Internat. J. Quantum Chem.
45 (1993), 3--14.
by forward recursion, Internat. J. Quantum Chem.
45 (1993), 3--14.
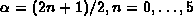 , Angew.
Informatik 17 (1975), 30--32.
, Angew.
Informatik 17 (1975), 30--32.
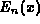 , J. Res. Nat.
Bur. Standards 78B (1974), 199--216.
, J. Res. Nat.
Bur. Standards 78B (1974), 199--216.