

| Matrix Generator MVMTLS | |
|---|---|
| Source: | S. Godet-Thobie, CERFACS and C. Bès, Aerospatiale, France |
| Discipline: | Aeroelasticity |
| Language: | Fortran |
| Output format: | matrix-vector multiply |
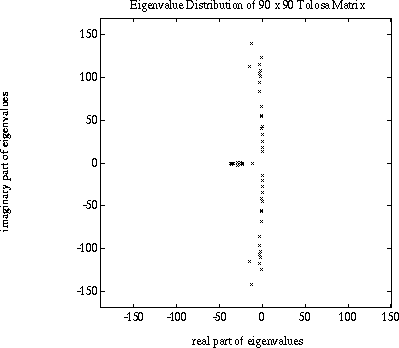
The Tolosa matrix arises in the stability analysis of a model of an airplane in flight. The interesting modes of this system are described by complex eignevalues whose imaginary parts lie in a prescribed frequency range. The task is to compute the eigenvalues with largest imaginary parts. The problem has been analyzed at CERFACS (Centre European de Recherche et de Formation Avancee en Calcul Scientifique) in cooperation with the Aerospatiale Aircraft division.
The matrix is a sparse 5 x 5 block matrix of order n = 90 + 5k. In practice, k is around 104. When n = 90, each block is of dimension 18 x 18 and
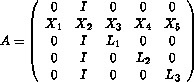
where 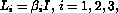 and
and 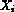 and
and 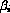 are given data. In general,
are given data. In general,
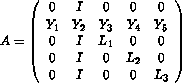
where
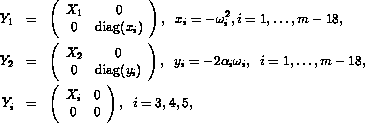
and
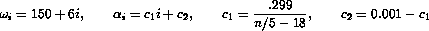
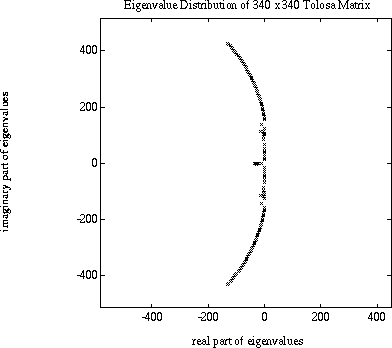
The following figures show the eigenvalue distribution of Tolosa matrices of orders 90 and 340.
Parameters:
| N | order of the matrix. Must be 90+5K for some nonnegative integer K. |
![[tols90 Icon]](tols90_tiny.gif) TOLS90 (real unsymmetric, 90 by 90, 1746 nonzeros) Parameters: N=90
TOLS90 (real unsymmetric, 90 by 90, 1746 nonzeros) Parameters: N=90
![[tols340 Icon]](tols340_tiny.gif) TOLS340 (real unsymmetric, 340 by 340, 2196 nonzeros) Parameters: N=340
TOLS340 (real unsymmetric, 340 by 340, 2196 nonzeros) Parameters: N=340
![[tols1090 Icon]](tols1090_tiny.gif) TOLS1090 (real unsymmetric, 1090 by 1090, 3546 nonzeros) Parameters: N=1090
TOLS1090 (real unsymmetric, 1090 by 1090, 3546 nonzeros) Parameters: N=1090
![[tols2000 Icon]](tols2000_tiny.gif) TOLS2000 (real unsymmetric, 2000 by 2000, 5184 nonzeros) Parameters: N=2000
TOLS2000 (real unsymmetric, 2000 by 2000, 5184 nonzeros) Parameters: N=2000
![[tols4000 Icon]](tols4000_tiny.gif) TOLS4000 (real unsymmetric, 4000 by 4000, 8784 nonzeros) Parameters: N=4000
TOLS4000 (real unsymmetric, 4000 by 4000, 8784 nonzeros) Parameters: N=4000
[ Home ] [ Search ] [ Browse ] [ Resources ]
Last change in this page: Wed Sep 22 13:37:33 US/Eastern 2004 [Comments: ]