

| Matrix Generator MVMRWK | |
|---|---|
| Source: | G.W. Stewart, University of Maryland |
| Discipline: | Probability theory and its applications |
| Language: | Fortran |
| Output format: | matrix-vector multiply |
Consider a random walk on an (m+1) × (m+1) triangular grid, illustrated below for m = 6.
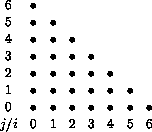
The points of the grid are labeled 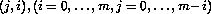 . From the point (j,i), a transition may take place to one of the four adjacent points (j+1,i), (j,i+1), (j-1,i), (j,i-1). The probability of jumping to either of the nodes (j-1,i) or (j,i-1) is
. From the point (j,i), a transition may take place to one of the four adjacent points (j+1,i), (j,i+1), (j-1,i), (j,i-1). The probability of jumping to either of the nodes (j-1,i) or (j,i-1) is

with the probability being split equally between the two nodes when both nodes are on the grid. The probability of jumping to either of the nodes (j+1,i) or (j,i+1) is

with the probability again being split when both nodes are on the grid. If the (m+1)(m+2)/2 nodes (j,i) are numbered 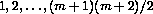 in some fashion, then the random walk can be expressed as a finite Markov chain with transition matrix A of order
in some fashion, then the random walk can be expressed as a finite Markov chain with transition matrix A of order 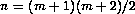 consisting of the probabilities akl of jumping from node l to node k (A is actually the transpose of the usual transition matrix; see [Feller]).
consisting of the probabilities akl of jumping from node l to node k (A is actually the transpose of the usual transition matrix; see [Feller]).
We are primarily interested in the steady state probabilities of the chain, which is ordinarily the appropriately scaled eigenvector corresponding to the eigenvalue unity.
Figure 1 shows the sparsity pattern of the resulted random walk matrix of order 136 (i.e. m=15).
To calculate the i-th element of the vector Ax one need only regard the components of q as the average number of individuals at the nodes of the grid and use the probabilities (5) and (6) to calculate how many individuals will be at node i after the next transition.
Fortran calling sequence for Y = AX.
Parameters:
| N | order of the matrix. Must me (M+1)(M+2)/2 for some positive M. |
![[rw136 Icon]](rw136_tiny.gif) RW136 (real unsymmetric, 136 by 136, 479 nonzeros) Parameters: N=136
RW136 (real unsymmetric, 136 by 136, 479 nonzeros) Parameters: N=136
![[rw496 Icon]](rw496_tiny.gif) RW496 (real unsymmetric, 496 by 496, 1859 nonzeros) Parameters: N=496
RW496 (real unsymmetric, 496 by 496, 1859 nonzeros) Parameters: N=496
![[rw5151 Icon]](rw5151_tiny.gif) RW5151 (real unsymmetric, 5151 by 5151, 20199 nonzeros) Parameters: N=5151
RW5151 (real unsymmetric, 5151 by 5151, 20199 nonzeros) Parameters: N=5151
[ Home ] [ Search ] [ Browse ] [ Resources ]
Last change in this page: Wed Sep 22 13:37:32 US/Eastern 2004 [Comments: ]