Matrix Generator MVMISG

MVMISG: Ising Model for Ferromagnetic Materials

from the NEP Collection

Matrix Generator MVMISG
Source:	B. Friedman
Discipline:	Material science
Language:	Fortran
Output format:	matrix-vector multiply

This test matrix is from the analysis of the Ising model for ferromagnetic materials. The matrix A is the product of the two 2m × 2m matrices K and L,

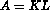
where

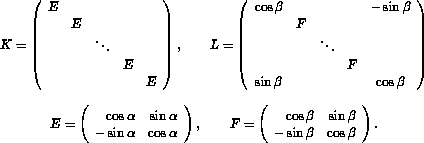
K= block diagonal matrix with E's on the diagonal; L=matrix with cos beta in upper left and lower right corners, +/1 sin beta in lower left and upper right cornders and F in remaining diagonals; E=Matrix((cos alpha, sin alpha), (-sin alpha, cos alpha)); F = Matrix((cos beta, sin beta),(-sin beta, cos beta))

It can be shown that the eigenvalues of A are the 2m numbers that are obtained by computing the eigenvalues of the m 2 by 2 matrices

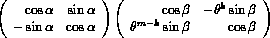
F times Matrix((cos beta, -theta^k sin beta),(theta^(m-k) sin beta, cos beta))

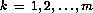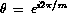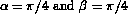for k=1,2,...m , where theta=e^(2 pi i/m) . Figure 1 shows the eigenvalue distribution of 100 by 100 Ising matrix with alpha=pi/4 and beta=pi/4 .

The following is the FORTRAN calling sequence for forming matrix-vector AX or A^TX: Fortran calling sequence.

This Ising model was proposed to explain properties of ferromagnets but since then it has found application to topics in chemistry and biology as well as physics. For any reader unfamiliar with the model an excellent introduction is [B. A. Cipra].

A numerical method for approximating the leading eigenvalues of 2D Ising models using a transfer matrix of order 2ⁿ with n = 30 is reported in [B. Parlett and W. Heng].

We plan to include the transfer matrix in the future version of this collection.

Parameters:

N	order of the matrix (must be even)
ALPHA	first angle
BETA	second angle

MVMISG: Ising Model for Ferromagnetic Materials

from the NEP Collection

Links: