The Matrix Market

Home Search Browse Resources

H2PLUS: Model of H2+ in an Electromagnetic Field

from the NEP Collection

Set H2PLUS
Source: S.I. Chu, University of Kansas
Discipline: Quantum chemistry

The physical problem is to determine the laser-induced molecular resonance states of H2+ in an electro-magnetic field. The complex-scaling technique applied to the self-adjoint Hamiltonian from quantum mechanics yields a complex symmetric eigenvalue problem 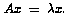A x = lambda x. To determine the stability of the state, Floquet exponents are computed by the standard Fourier-grid method.

Figure 1 displays the eigenvalues computed by the QR algorithm for the matrix QC2534.

Matrices in this set:

The Matrix Market is a service of the Mathematical and Computational Sciences Division / Information Technology Laboratory / National Institute of Standards and Technology.

[ Home ] [ Search ] [ Browse ] [ Resources ]

Last change in this page: Wed Sep 22 13:37:25 US/Eastern 2004 [Comments: ]