Matrix Set BRUSSEL

BRUSSEL: Reaction-diffusion Brusselator Model

from the NEP Collection

Set BRUSSEL
Source:	K. Meerbergen, Katholieke Universiteit Leuven, Belgium and A. Spence, University of Bath, UK
Discipline:	Chemical engineering

The equations

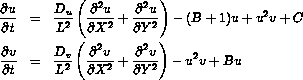
du/dt=D_u/L^2 (d^2u/dX^2 + d^2u/dY^2) - (B+1)u + u^2 v+C; dv/dt = D_v/L^2(d^2v/dX^2 + d^2u/dY^2) - u^2 v + B u

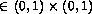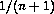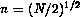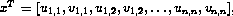for u and epsilon (0,1) cross (0,1) with homogeneous Dirichlet boundary conditions form a 2D reaction-diffusion model where u and v represent the concentrations of two reactions. The equations are discretized with central differences with grid size h_u = h_v = 1/(n+1) with n=(N/2)^(1/2) . For $x^T=[u_{1,1}, v_{1,1},u_{1,2},v_{1,2},...,u_{n,n},v_{n,n}$ , the discretized equations can be written as 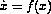x dot = f(x) . One wants to compute the rightmost eigenvalues of the Jacobi matrix 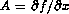A=df/dx , with the parameters B = 5.45, C = 2, D_u = 0.004, D_v = 0.008. The parameter L varies.