 [caption]
[caption]
 [caption]
[caption]
PHAML version 1.20.0 can be downloaded as the file phaml-1.20.0.tar.gz (10.8 MB) for Unix systems and MS Windows with Cygwin. When unpacked, it will place everything in a directory named phaml-1.20.0.
The User's Guide is included as a pdf file in the distribution, or it can be obtained here as a pdf file (3.7 MB). There is also a two page Quick Start guide.
PHAML can optionally use PETSc for alternative linear system solvers, and uses
SLEPc for eigenvalue problems. Unfortunately, in the past PETSc has often made
changes to the API that require
changes in PHAML. Since PHAML is no longer under development, it is possible
that a version of PETSc released after the final release of PHAML will not
work with PHAML. If you find this to be the case, you can obtain the last
version of PETSc known to work with PHAML here. If you get PETSc from here,
you must also get SLEPc from here (if you use
SLEPc) because the SLEPc version must agree with the PETSc version.
petsc-lite-3.9.3.tar.gz (11.6 MB)
slepc-3.9.2.tar.gz (4.5 MB)
Send questions, bug reports, etc. to [email protected].
PHAML is in the public domain and not subject to copyright. Please see
the LICENSE file.
The primary goal of the PHAML (Parallel Hierarchical
Adaptive MultiLevel method) project is to develop
new methods and software for the efficient solution of 2D elliptic partial
differential equations (PDEs) on distributed memory parallel computers and
multicore computers using
adaptive mesh refinement and multigrid solution techniques.
The main accomplishments and features of PHAML are:
With its wide range of features and choices, PHAML can be (and has been)
used for many purposes including:
The research performed by the PHAML project has resulted in several
advances in numerical methods for the solution of PDEs on parallel
computers. Further details can be found by clicking on the link for each
topic.
The methods developed by the PHAML project have been implemented in the
research code PHAML. PHAML is written in Fortran 90 and uses
MPI
for message passing and OpenMP for shared memory parallelism.
Further details can be found by clicking on the link for each
topic.
If you do not have the software to read the available formats, an
alternate format or a paper copy of these documents will be mailed to you
if requested from
William Mitchell.
Mitchell, W.F., PHAML User's Guide , NISTIR 7374 , 2006.
(original, pdf, 3.2M )
(latest revision, pdf)
Mitchell, W.F. and McClain, M.A., A Comparison of hp-Adaptive Strategies for Elliptic
Partial Differential Equations, ACM
Transactions on Mathematical Software , 41 (1), 2014.
(preprint, pdf, 792K)
(
link to journal)
Mitchell, W.F. and McClain, M.A., A Comparison of hp-Adaptive Strategies for Elliptic
Partial Differential Equations (long version),
NISTIR 7824, 2011.
( pdf, 33M, 215 pages)
Mitchell, W.F. A Collection of 2D Elliptic Problems for Testing Adaptive
Algorithms, NISTIR 7668, 2010.
( pdf, 1.6M)
Mitchell, W.F. and McClain, M.A. A Survey of hp-Adaptive Strategies for Elliptic Partial
Differential Equations, in Recent Advances
in Computational and Applied Mathematics (T. E. Simos, ed.), Springer,
2011, pp. 227-258.
(preprint, pdf, 16M)
Mitchell, W.F., A Refinement-tree Based Partitioning Method for Dynamic Load Balancing
with Adaptively Refined Grids , J. Par. Dist. Comp., 67 (4),
2007, pp. 417-429.
( pdf, 2.5M)
( link to journal )
Mitchell, W.F., Hamiltonian Paths Through Two- and Three-Dimensional Grids ,
NIST J. Res. , 110, (2005), pp. 127-136.
( gzipped postscript, 79k)
Mitchell, W.F., Parallel Adaptive Multilevel Methods with Full Domain Partitions ,
App. Num. Anal. and Comp. Math., 1, (2004), pp. 36-48.
( gzipped postscript, 286k)
Mitchell, W.F., The Design of a Parallel Adaptive Multi-Level Code in Fortran 90,
Proceedings of the 2002 International Conference on Computational
Science, 2002.
( gzipped postscript, 50k)
Mitchell, W.F., Adaptive Grid Refinement and Multigrid on Cluster Computers,
Proceedings of the 15th International Parallel and
Distributed Processing Symposium, IEEE Computer Society Press,
2001.
( gzipped postscript, 200k)
Mitchell, W.F., A Comparison of Three Fast Repartition Methods
for Adaptive Grids, Proceedings of the Ninth SIAM Conference
on Parallel Processing for Scientific Computing, 1999.
( gzipped postscript, 50k)
Mitchell, W.F., A Parallel Multigrid Method Using the Full Domain Partition,
Electronic Transactions on Numerical Analysis, 6 (1998)
pp. 224-233, special
issue for proceedings of the 8th Copper Mountain
Conference on Multigrid Methods.
( gzipped postscript, 100k)
Mitchell, W.F., The Full Domain Partition Approach to Parallel Adaptive Refinement,
IMA Volumes in Mathematics and its Applications, 113,
Springer-Verlag, 1998, pp. 151-162. Volume devoted to the IMA Workshop on Grid
Generation and Adaptive Algorithms.
( gzipped postscript, 138k)
Mitchell, W.F., The Refinement-Tree Partition for Parallel Solution of
Partial Differential Equations, NIST Journal of Research,
103 (1998), pp. 405-414.
( gzipped postscript, 96k)
Mitchell, W.F., The Full Domain Partition Approach to Distributing
Adaptive Grids, Applied Numerical Mathematics, 26 (1998)
pp. 265-275, special issue for the proceedings of Grid Adaptation in
Computational PDEs: Theory and Applications.
(gzipped postscript, 102k)
Mitchell, W.F., The Full Domain Partition Approach for Parallel Multigrid on
Adaptive Grids, Proceedings of the Eighth SIAM Conference on
Parallel Processing for Scientific Computing, 1997.
(gzipped postscript, 179k)
Mitchell, W.F., Refinement Tree Based Partitioning for
Adaptive Grids, Proceedings of the 7th SIAM Conference
on Parallel Processing for Scientific Computing, SIAM, 1995,
pp. 587-592.
(gzipped postscript, 75k)
Mitchell, W.F., Optimal multilevel iterative methods for adaptive
grids, SIAM J. Sci. Statist. Comput. 13 (1992),
pp. 146-167.
Mitchell, W.F., Adaptive refinement for arbitrary finite element
spaces with hierarchical bases, J. Comp. Appl. Math. 36
(1991), pp. 65-78.
Mitchell, W.F. A comparison of adaptive refinement techniques
for elliptic problems. ACM Trans. Math. Soft. 15 (1989),
pp. 326-347.
Mitchell, W.F., Unified multilevel adaptive finite element
methods for elliptic problems, Ph.D. thesis, Technical report
UIUCDCS-R-88-1436, Department of Computer Science, University
of Illinois, Urbana, IL, 1988.
(
gzipped postscript, 194k)
Development status: Not Maintained
Last change to this page: August 28, 2018
Date this page created: 1997
Home Page
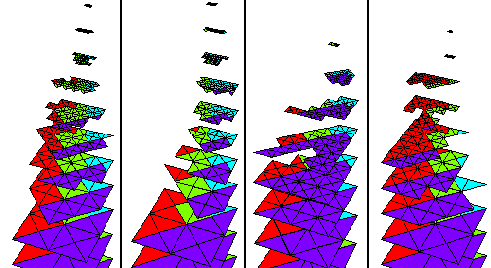
An adaptive multilevel grid on four processors. Each
panel shows the grid on one processor. The colors indicate which
processor is the "owner" of the triangles. From left to right, the
processor colors are green, cyan, purple and red. The grids have been
separated by refinement level to show the multigrid sequence.
Goals

PHAML solution on four processors of an
equation with a singular boundary condition. The colors or shades of gray
indicate the region assigned to each processor.
PHAML Methods
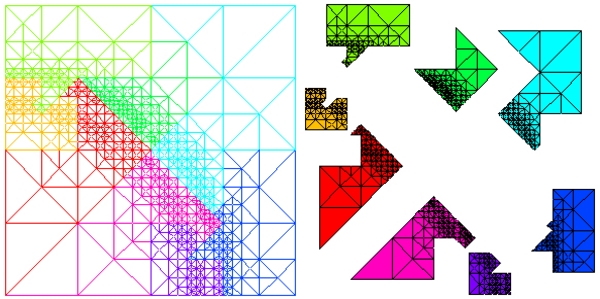
Two visualizations of an 8 processor partition of a grid adapted to a
circular wave front.
PHAML Software

A solution computed on eight processors.
Publications
Contact