Michael J. Donahue: Micromagnetic Modeling
Due to long-range magnetic interactions and shape effects, it is not computational feasible to model device magnetization behavior at the atomic level. Micromagnetic modeling operates instead at a slighly larger scale, large enough to allow a continous approximation for the magnetization, but small enough to reveal fine details about device transitions.
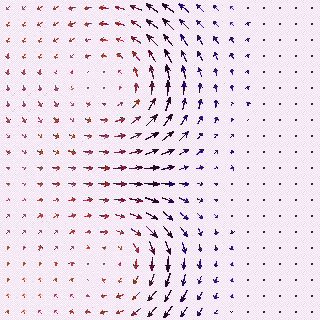
The above image is sample output of a micromagnetic modeling program I
developed with
Bob McMichael, illustrating one step in the spontaneous
magnetization of a 40 nm x 40 nm iron whisker. The arrows represent
magnetization direction; the component perpendicular to the viewing
plane is color coded (red is into the plane, blue is out of the plane,
black is in-plane). In the initial configuration, the left half of
the whisker was magnetized into the plane, the right half magnetized
out of the plane. The dimensions of the whisker are too small to
support multiple magnetic domains, and so as the system evolves the
magnetization gradually aligns perpendicular to the viewing plane. I
have put together an MPEG movie (2995695
bytes) showing the complete process. (Note: Your mpeg viewer must
support I, B and P frames to properly view this movie.)
I am also closely associated with the µMag Micromagnetic Modeling Activity Group, and have recently been collecting results from various researchers on the µMag first standard problem. I have put together two MPEG movies of a micromagnetic simulation of the first standard problem, showing the magnetization of a 1 micron x 2 micron x 20 nm thick permalloy rectangle, as it is swept through a hysteresis loop. In the first movie (3950790 bytes), the external field is applied 1 degree counterclockwise (in the film plane) to the short axis, stepping from +50 mT to -50 mT and back to +50 mT, in 1 mT steps. The second movie (2610081 bytes) is analogous, except that the external field is applied 1 degree counterclockwise from the long axis. Each frame is a relaxed state, and the calculation mesh consists of 50 x 100 20 nm cubes.
I have also put together a third movie (3897923 bytes) showing the transition across the coercive point, illustrating the details of the transition between frames 55 and 56 of the "second movie." The field is stepped at the beginning of the animation from -4 mT to -5 mT. Successive frames represent 10 iterations of the ODE solver, i.e., these are not relaxed states. The step size is variable, but is typically 4-10 psec (i.e., 40-100 psec per displayed frame).
Don Porter and I have developed a public
domain release of the micromagnetic software used in the above
simulations. This is the OOMMF (Object Oriented
Micromagnetic Framework) project. The next pictures show sample
output from the 3D micromagnetic solver in that package, as applied to
µMag
Standard Problem #3. The images are orthogonal slices through the
center of an equilibrium vortex state for a cubic magnetic particle,
with edge dimension equal to 8.47 times the magnetostatic exchange
length, i.e., close to the cross-over point where the energy of the
vortex and flower states are equal.


In these pictures, only every third computational cell is displayed.
The complete data file may be viewed with
the OOMMF tools.
Steve Russek of PML has used OOMMF to study high-speed magnetization reversal in thin NiFe films. Here is a QuickTime movie (6693998 bytes) of the reversal of a 10 nm thick NiFe particle, with 2.5 x 0.5 micron in-plane dimensions. There is a constant 0.5 mT bias field upward along the 0.5 micron axis, and a 30 mT step field is applied along the 2.5 micron axis, first to the left, and then to the right. Before each pulse the magnetization is allowed to relax into an equilibrium state with only the bias field applied. The total simulation time is 6 ns (forward and back), with the bulk of the reversal occuring in 1 ns (in each direction). There are additional movies on the OOMMF Movie Page.
Other Micromagnetic Web Pages
- µMag Micromagnetic Modeling Activity Group (NIST)
- Object Oriented Micromagnetic Framework (OOMMF) project (NIST)
Date created: September 12, 2016 | Last updated: September 12, 2016 Contact: Webmaster