Waves Impinging on a Planar Boundary
For a rectangular domain, with a point source excited by a Gaussian pulse
and periodic boundary conditions in one direction, we compared (in the
other direction) exact nonreflecting boundary conditions, as implemented
by our method, with Berenger-type perfectly matched layers (PML).
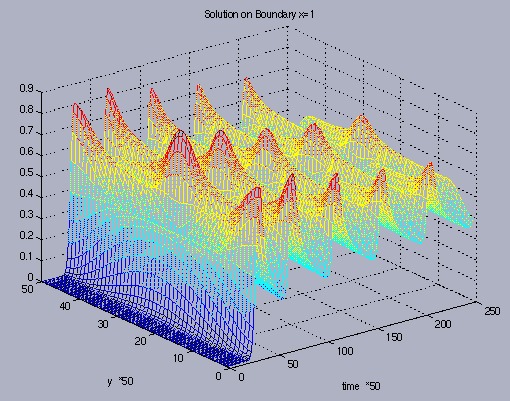
On one nonreflecting boundary, as a function of time, the solution
is illustrated below.
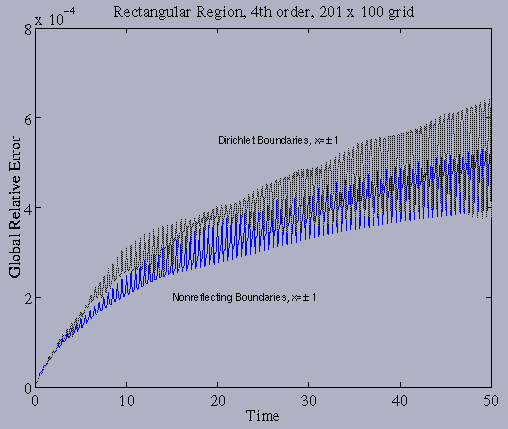
The global relative error of the computed solution, with our implementation
of the exact nonreflecting boundary conditions and with exact Dirichlet
boundary conditions, is shown below.
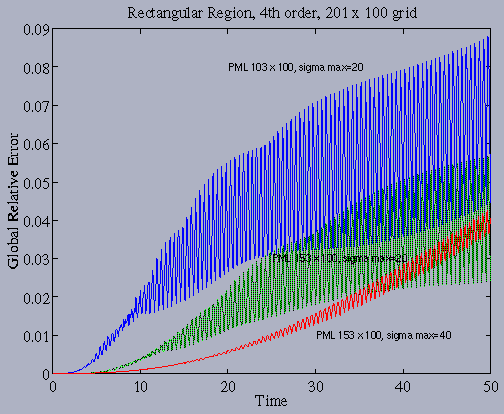
Finally, the global relative error of the computed solution, with different
perfectly matched layers, is shown. Of several layer thicknesses and
attenuations that we tried, the three shown produced the lowest error.
Note that the error is quite substantial, approximately one hundredfold
worse than with our implementation of the exact nonreflecting boundary
conditions. In fact, while for the exact boundary conditions our
implementation is fourth-order convergent, with PML the solution does
not converge to the correct answer.
Back to Time-Domain Algorithms for Computational Electromagnetics
Bradley K Alpert
Last modified: Fri Jul 14 12:11:40 MDT 2000