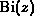 nor
the Bessel function of the second kind
nor
the Bessel function of the second kind 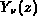 has a useful
role when the argument z is not real; compare
[ Olv74, Chapters 7 and 11]
.
has a useful
role when the argument z is not real; compare
[ Olv74, Chapters 7 and 11]
.
D. W. Lozier and F. W. J. Olver
7. Future Trends
Great progress has been made in recent years in the construction of software for generating the special functions, yet enormous gaps remain for functions having variable parameters in addition to the argument. This is especially true when the variables are complex. In this concluding section we offer some general suggestions concerning future work in this area.
First, because of the sheer magnitude of the effort
required, there should be a perceived physical or other applied
need before a decision is made to embark on the construction of
extensive new software for functions of two or more variables. At
present there are simply too many gaps to fill to be able to
indulge in the luxury of arbitrary selection. Moreover, great
care should be exercised in the choice of actual functions to be
generated. For example, neither the Airy function 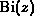 nor
the Bessel function of the second kind
nor
the Bessel function of the second kind 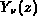 has a useful
role when the argument z is not real; compare
[ Olv74, Chapters 7 and 11]
.
has a useful
role when the argument z is not real; compare
[ Olv74, Chapters 7 and 11]
.
Second, coverage of a chosen region should be dictated by uniform accuracy requirements (in an appropriate measure), not by the limitations of the methods that happen to be used. At the very least it is frustrating for users to discover that the precision yielded by a package varies widely, or worse still disappears altogether, in parts of the claimed regions of coverage.
Third, the potential offered by the ongoing increase in power of computers should be exploited with a view to reducing the number and complexity of algorithms to be used. This includes, for example, the use of parallel or vector methods for summing series [ Kar91] or solving differential or difference equations [ LO93] .
Fourth---and here we are looking further into the future---the use of systems of computer arithmetic other than floating-point should be considered. The floating-point system has two disadvantages which become especially annoying and time-consuming in the construction of special-function software. One is that the associated error measure, relative precision, is quite inappropriate in the neighborhoods of zeros. The other stems from failure due to overflow or underflow: here the usual remedy of rescaling can be difficult to apply, owing to the extremely varied asymptotic behavior of functions of several variables. A system of computer arithmetic that is capable of overcoming both problems in an elegant manner is the so-called level-index system [ COT89] .
Lastly, any new algorithm or package should be documented
fully. It should also be subjected to exhaustive testing
procedures, and these, too, need to be documented. Indeed, the
proposed testing procedures should be considered at an early
stage in the planning of the main algorithms![]() . There are so many pitfalls in the
construction of algorithms for the special functions that the use
of undocumented or insufficiently tested packages is a risky
proposition
. There are so many pitfalls in the
construction of algorithms for the special functions that the use
of undocumented or insufficiently tested packages is a risky
proposition![]() .
.
The original abstract follows.
Higher transcendental functions continue to play varied and important roles in investigations by engineers, mathematicians, scientists and statisticians. The purpose of this paper is to assist in locating useful approximations and software for the numerical generation of these functions, and to offer some suggestions for future developments in this field.
Applied and Computational Mathematics Division, National Institute of Standards and Technology, Gaithersburg, Md 20899
E-mail address: [email protected]
Institute for Physical Science and Technology, University of Maryland, College Park, MD 20742
E-mail address: [email protected]
The research of the second author has been supported by NSF Grant CCR 89-14933.
1991 Mathematics Subject Classification. Primary 65D20; Secondary 33-00.