Press
here
to get the full document in PostScript format.
Press
here
to get this subdocument in PostScript format.
Numerical Evaluation of Special Functions
D. W. Lozier and F. W. J. Olver
5.5. Hypergeometric and Confluent Hypergeometric Functions
.
5.5.1. Hypergeometric Functions.
Intermediate Libraries:
[ Bak92]
,
[ Mos89]
,
[ ULI90]
.
Comprehensive Libraries:
Numerical Recipes.
Interactive Systems:
Mathematica.
5.5.2. Confluent Hypergeometric Functions.
Software Packages:
[ BS80, Fortran]
,
[ NPB92a, Fortran]
,
[ NT84, Fortran]
,
[ Tem83, Algol]
.
Intermediate Libraries:
[ Bak92]
,
[ Mos89]
,
[ ULI90]
.
Comprehensive Libraries:
SLATEC.
Interactive Systems:
Mathematica.
5.5.3. Other Hypergeometric Functions.
Algorithms:
[ PBN93]
.
Software Packages:
[ CM84, Pascal]
.
Intermediate Libraries:
[ Bak92]
,
[ Mos89]
.
Interactive Systems:
Maple,
Mathematica.
5.5.4. Articles.
[ BMOF92]
,
[ CG89]
,
[ Luk75]
,
[ Luk77a]
,
[ Nem74]
,
[ NPB92b]
,
[ Wim74]
.
References
- Bak92
-
L. Baker, C mathematical function handbook, McGraw-Hill, Inc., New
York, 1992, includes diskette.
- BMOF92
-
E. Badralexe, P. Marksteiner, Y. Oh, and A. J. Freeman, Computation of the
Kummer functions and Whittaker functions by using Neumann type series
expansions, Comput. Phys. Comm. 71 (1992), 47--55.
- BS80
-
K. L. Bell and N. S. Scott, Coulomb functions (negative energies
), Comput. Phys. Comm. 20 (1980), 447--458.
- CG89
-
G. Chiocchia and B. Gabutti, A new transformation for computing
hypergeometric series and the exact evaluation of the transonic adiabatic
flow over a smooth bump, Comput. & Fluids 17 (1989), no. 1,
13--23.
- CM84
-
A. P. Clarke and W. Marwood, A compact mathematical function package,
Austral. Comput. J. 16 (1984), 107--114.
- Luk75
-
Y. L. Luke, Mathematical functions and their approximations, Academic
Press, New York, 1975.
- Luk77
-
Y. L. Luke, Algorithms for rational approximations for a confluent
hypergeometric function, Utilitas Math. 11 (1977), 123--151.
- Mos89
-
S. L. B. Moshier, Methods and programs for mathematical functions, Ellis
Horwood Limited, Chichester, 1989, separate diskette.
- Ném74
-
G. Németh, Expansion of generalized hypergeometric functions in
Chebyshev polynomials, Collection of Scientific Papers in Collaboration of
Joint Institute for Nuclear Research, Dubna, USSR and Central Research
Institute for Physics, Budapest, Hungary, Hungarian Academy of Sciences,
Central Research Institute for Physics, Budapest, 1974, reference No.
KFKI-74-34, pp. 57--91.
- NPB92a
-
M. Nardin, W. F. Perger, and A. Bhalla, Algorithm 707. CONHYP : A
numerical evaluator of the confluent hypergeometric function for complex
arguments of large magnitudes, ACM Trans. Math. Software 18 (1992),
345--349.
- NPB92b
-
M. Nardin, W. F. Perger, and A. Bhalla, Numerical evaluation of the
confluent hypergeometric function for complex arguments of large magnitudes,
J. Comput. Appl. Math. 39 (1992), 193--200.
- NT84
-
C. J. Noble and I. J. Thompson, COULN, A program for evaluating
negative energy Coulomb functions, Comput. Phys. Comm. 33 (1984),
413--419.
- PBN93
-
W. F. Perger, A. Bhalla, and M. Nardin, A numerical evaluator for the
generalized hypergeometric series, Comput. Phys. Comm. 77 (1993),
249--254.
- Tem83
-
N. M. Temme, The numerical computation of the confluent hypergeometric
function
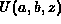 , Numer. Math. 41 (1983), 63--82.
, Numer. Math. 41 (1983), 63--82.
- ULI90
-
Mathematical function library for Microsoft--C, United Laboratories,
Inc., John Wiley & Sons, 1990, includes diskettes. Edition also
exists in Fortran (1989).
- Wim74
-
J. Wimp, On the computation of Tricomi's
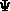 function, Computing
13 (1974), 195--203.
function, Computing
13 (1974), 195--203.
Abstract:
This document is an excerpt from the current hypertext version of
an article that appeared in Walter Gautschi (ed.),
Mathematics of Computation 1943--1993: A Half-Century of
Computational Mathematics, Proceedings of Symposia in
Applied Mathematics 48, American Mathematical Society,
Providence, RI 02940, 1994.
The symposium was held at the University of British Columbia
August 9--13, 1993, in honor of the fiftieth anniversary of
the journal Mathematics of Computation.
The original abstract follows.
Higher transcendental functions continue to play varied and
important roles in investigations by engineers, mathematicians,
scientists and statisticians.
The purpose of this paper is to assist in locating useful approximations
and software for the numerical generation of these functions, and to
offer some suggestions for future developments in this field.
Applied and Computational Mathematics Division,
National Institute of Standards and Technology,
Gaithersburg, Md 20899
E-mail address: dlozier@nist.gov
Institute for Physical Science and Technology,
University of Maryland,
College Park, MD 20742
E-mail address: olver@bessel.umd.edu
The research of the second author has been supported by NSF
Grant CCR 89-14933.
1991 Mathematics Subject Classification. Primary 65D20;
Secondary 33-00.
Daniel W Lozier
Fri Apr 7 14:13:03 EDT 1995
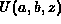 , Numer. Math. 41 (1983), 63--82.
, Numer. Math. 41 (1983), 63--82.
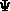 function, Computing
13 (1974), 195--203.
function, Computing
13 (1974), 195--203.
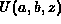 , Numer. Math. 41 (1983), 63--82.
, Numer. Math. 41 (1983), 63--82.
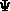 function, Computing
13 (1974), 195--203.
function, Computing
13 (1974), 195--203.