Press
here
to get the full document in PostScript format.
Press
here
to get this subdocument in PostScript format.
Numerical Evaluation of Special Functions
D. W. Lozier and F. W. J. Olver
5.2. Coulomb Wave Functions
.
5.2.1. Real Arguments and Parameters.
Algorithms:
[ CH70b]
,
[ She74]
.
Software Packages:
[ Bar76, Fortran]
,
[ Bar81b, Fortran]
,
[ Bar82b, Fortran]
,
[ BDG+72, Fortran]
,
[ BS80, Fortran]
,
[ NT84, Fortran]
,
[ Sea82, Fortran]
.
Intermediate Libraries:
[ Bak92]
.
5.2.2. Complex Arguments and Parameters.
Software Packages:
[ TB85, Fortran]
,
[ TR69, Fortran]
.
5.2.3. Articles.
[ AS92]
,
[ Bar81a]
,
[ Bar82a]
,
[ Bar82c]
,
[ Gau69b]
,
[ Kol72b, includes survey]
,
[ Nes84]
,
[ Pex70]
,
[ SG72]
,
[ TB86]
.
References
- AS92
-
J. Abad and J. Sesma, Computation of Coulomb wave functions at low
energies, Comput. Phys. Comm. 71 (1992), 110--124.
- Bak92
-
L. Baker, C mathematical function handbook, McGraw-Hill, Inc., New
York, 1992, includes diskette.
- Bar76
-
A. R. Barnett, RCWFF---A modification of the real Coulomb
wavefunction program RCWFN, Comput. Phys. Comm. 11 (1976), 141--142.
- Bar81a
-
A. R. Barnett, An algorithm for regular and irregular Coulomb and
Bessel functions of real order to machine accuracy, Comput. Phys. Comm.
21 (1981), 297--314.
- Bar81b
-
A. R. Barnett, KLEIN : Coulomb functions for real
 and
positive energy to high accuracy, Comput. Phys. Comm. 24 (1981),
141--159.
and
positive energy to high accuracy, Comput. Phys. Comm. 24 (1981),
141--159.
- Bar82a
-
A. R. Barnett, Continued-fraction evaluation of Coulomb functions
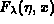 ,
, 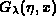 and their derivatives, J.
Comput. Phys. 46 (1982), 171--188.
and their derivatives, J.
Comput. Phys. 46 (1982), 171--188.
- Bar82b
-
A. R. Barnett, COULFG : Coulomb and Bessel functions and their
derivatives, for real arguments, by Steed's method, Comput. Phys. Comm.
27 (1982), 147--166.
- Bar82c
-
A. R. Barnett, High-precision evaluation of the regular and irregular
Coulomb wavefunctions, J. Comput. Appl. Math. 8 (1982), 29--33.
- BDG
 72
72 -
C. Bardin, Y. Dandeu, L. Gauthier, J. Guillerman, T. Lena, and J.-M. Pernet,
Coulomb functions in the entire
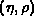 --plane, Comput. Phys.
Comm. 3 (1972), 73--87.
--plane, Comput. Phys.
Comm. 3 (1972), 73--87.
- BS80
-
K. L. Bell and N. S. Scott, Coulomb functions (negative energies
), Comput. Phys. Comm. 20 (1980), 447--458.
- CH70
-
W. J. Cody and K. E. Hillstrom, Chebyshev approximations for the Coulomb
phase shift, Math. Comp. 24 (1970), 671--677, for corrigendum, see
same journal v. 26 (1972), p. 1031.
- Gau69
-
W. Gautschi, An application of minimal solutions of three-term recurrences
to Coulomb wave functions, Aequationes Math. 2 (1969), 171--176.
- Köl72
-
K. S. Kölbig, Remarks on the computation of Coulomb wavefunctions,
Comput. Phys. Comm. 4 (1972), 214--220.
- Nes84
-
R. K. Nesbet, Algorithms for regular and irregular Coulomb and Bessel
functions, Comput. Phys. Comm. 32 (1984), 341--347.
- NT84
-
C. J. Noble and I. J. Thompson, COULN, A program for evaluating
negative energy Coulomb functions, Comput. Phys. Comm. 33 (1984),
413--419.
- Pex70
-
R. L. Pexton, Computer investigation of Coulomb wave functions, Math.
Comp. 24 (1970), 409--411.
- Sea82
-
M. J. Seaton, Coulomb functions analytic in the energy, Comput. Phys.
Comm. 25 (1982), 87--95.
- SG72
-
A. J. Strecok and J. A. Gregory, High precision evaluation of the
irregular Coulomb wave functions, Math. Comp. 26 (1972), 955--961.
- She74
-
V. B. Sheorey, Chebyshev expansions for wave functions, Comput. Phys.
Comm. 7 (1974), 1--12.
- TB85
-
I. J. Thompson and A. R. Barnett, COULCC : A continued-fraction
algorithm for Coulomb functions of complex order with complex arguments,
Comput. Phys. Comm. 36 (1985), 363--372.
- TB86
-
I. J. Thompson and A. R. Barnett, Coulomb and Bessel functions of
complex arguments and order, J. Comput. Phys. 64 (1986), 490--509.
- TR69
-
T. Tamura and F. Rybicki, Coulomb functions for complex energies, Comput.
Phys. Comm. 1 (1969), 25--30, for erratum see same journal v. 3 (1972),
p. 276.
Abstract:
This document is an excerpt from the current hypertext version of
an article that appeared in Walter Gautschi (ed.),
Mathematics of Computation 1943--1993: A Half-Century of
Computational Mathematics, Proceedings of Symposia in
Applied Mathematics 48, American Mathematical Society,
Providence, RI 02940, 1994.
The symposium was held at the University of British Columbia
August 9--13, 1993, in honor of the fiftieth anniversary of
the journal Mathematics of Computation.
The original abstract follows.
Higher transcendental functions continue to play varied and
important roles in investigations by engineers, mathematicians,
scientists and statisticians.
The purpose of this paper is to assist in locating useful approximations
and software for the numerical generation of these functions, and to
offer some suggestions for future developments in this field.
Applied and Computational Mathematics Division,
National Institute of Standards and Technology,
Gaithersburg, Md 20899
E-mail address: [email protected]
Institute for Physical Science and Technology,
University of Maryland,
College Park, MD 20742
E-mail address: [email protected]
The research of the second author has been supported by NSF
Grant CCR 89-14933.
1991 Mathematics Subject Classification. Primary 65D20;
Secondary 33-00.
Daniel W Lozier
Fri Apr 7 14:07:17 EDT 1995
 and
positive energy to high accuracy, Comput. Phys. Comm. 24 (1981),
141--159.
and
positive energy to high accuracy, Comput. Phys. Comm. 24 (1981),
141--159.
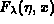 ,
, 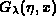 and their derivatives, J.
Comput. Phys. 46 (1982), 171--188.
and their derivatives, J.
Comput. Phys. 46 (1982), 171--188.
 72
72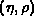 --plane, Comput. Phys.
Comm. 3 (1972), 73--87.
--plane, Comput. Phys.
Comm. 3 (1972), 73--87.
 and
positive energy to high accuracy, Comput. Phys. Comm. 24 (1981),
141--159.
and
positive energy to high accuracy, Comput. Phys. Comm. 24 (1981),
141--159.
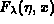 ,
, 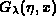 and their derivatives, J.
Comput. Phys. 46 (1982), 171--188.
and their derivatives, J.
Comput. Phys. 46 (1982), 171--188.
 72
72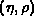 --plane, Comput. Phys.
Comm. 3 (1972), 73--87.
--plane, Comput. Phys.
Comm. 3 (1972), 73--87.