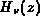 , Rend. Sem. Mat. Univ. Politec. Torino 32 (1975),
251--269.
, Rend. Sem. Mat. Univ. Politec. Torino 32 (1975),
251--269.
Press here to get the full document in PostScript format.
Press here to get this subdocument in PostScript format.
D. W. Lozier and F. W. J. Olver
5.12. Struve and Anger-Weber Functions .
5.12.1. Struve Functions or Integrals of Struve Functions.
Algorithms:
[ Luk69b] , [ Luk75] , [ Mac93] , [ New84] .
Intermediate Libraries:
[ Bak92] , [ Mos89] , [ ULI90] .
5.12.2. Integrals of Anger-Weber Functions.
Intermediate Libraries:
[ Bak92] .
5.12.3. Articles.
[ Zan75] .
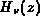 , Rend. Sem. Mat. Univ. Politec. Torino 32 (1975),
251--269.
, Rend. Sem. Mat. Univ. Politec. Torino 32 (1975),
251--269.
The original abstract follows.
Higher transcendental functions continue to play varied and important roles in investigations by engineers, mathematicians, scientists and statisticians. The purpose of this paper is to assist in locating useful approximations and software for the numerical generation of these functions, and to offer some suggestions for future developments in this field.
Applied and Computational Mathematics Division, National Institute of Standards and Technology, Gaithersburg, Md 20899
E-mail address: dlozier@nist.gov
Institute for Physical Science and Technology, University of Maryland, College Park, MD 20742
E-mail address: olver@bessel.umd.edu
The research of the second author has been supported by NSF Grant CCR 89-14933.
1991 Mathematics Subject Classification. Primary 65D20; Secondary 33-00.