Press
here
to get the full document in PostScript format.
Press
here
to get this subdocument in PostScript format.
Numerical Evaluation of Special Functions
D. W. Lozier and F. W. J. Olver
4.3. Exponential Integrals, Logarithmic Integral, Sine and Cosine Integrals
.
4.3.1. Exponential Integrals of Real Argument.
Algorithms:
[ Cle62]
,
[ CT69]
,
[ Luk69b]
,
[ Luk76]
.
Software Packages:
[ Amo80a, Fortran]
,
[ CMW63, Algol]
,
[ Gau73, Algol]
,
[ Pac70, Fortran]
,
[ SZ76, Fortran]
.
Intermediate Libraries:
[ Bak92]
,
[ ULI90]
.
Comprehensive Libraries:
IMSL,
NAG,
Numerical Recipes,
Scientific Desk,
SLATEC.
4.3.2. Logarithmic Integral of Real Argument.
Intermediate Libraries:
[ Bak92]
,
[ ULI90]
.
Comprehensive Libraries:
IMSL,
Scientific Desk,
SLATEC.
4.3.3. Sine and Cosine Integrals and Hyperbolic Sine and
Cosine Integrals of Real Argument.
Algorithms:
[ Luk69b]
.
Software Packages:
[ Bul67, Algol]
.
Intermediate Libraries:
[ Bak92]
,
[ Mos89]
,
[ ULI90]
.
Comprehensive Libraries:
IMSL,
NAG,
Numerical Recipes,
Scientific Desk.
4.3.4. Complex Arguments.
Algorithms:
[ Luk69b]
.
Software Packages:
[ Amo90a, Fortran]
.
Intermediate Libraries:
[ Bak92]
.
Interactive Systems:
Maple,
Mathematica.
4.3.5. Articles.
[ Amo80b]
,
[ Amo90b]
,
[ CT68]
,
[ TM68]
,
[ vdLT84]
.
References
- Amo80a
-
D. E. Amos, Algorithm 556. Exponential integrals, ACM Trans. Math.
Software 6 (1980), 420--428, for remark see same journal v. 9 (1983),
p. 525.
- Amo80b
-
D. E. Amos, Computation of exponential integrals, ACM Trans. Math.
Software 6 (1980), 365--377.
- Amo90a
-
D. E. Amos, Algorithm 683. A portable Fortran subroutine for
exponential integrals of a complex argument, ACM Trans. Math. Software
16 (1990), 178--182.
- Amo90b
-
D. E. Amos, Computation of exponential integrals of a complex argument,
ACM Trans. Math. Software 16 (1990), 169--177.
- Bak92
-
L. Baker, C mathematical function handbook, McGraw-Hill, Inc., New
York, 1992, includes diskette.
- Bul67
-
R. Bulirsch, Numerical calculation of the sine, cosine and Fresnel
integrals, Numer. Math. 9 (1967), 380--385.
- Cle62
-
C. W. Clenshaw, Chebyshev series for mathematical functions, National
Physical Laboratory Mathematical Tables, vol. 5, Her Majesty's Stationery
Office, London, 1962.
- CMW63
-
C. W. Clenshaw, G. F. Miller, and M. Woodger, Algorithms for special
functions I, Numer. Math. 4 (1963), 403--419.
- CT68
-
W. J. Cody and H. C. Thacher, Jr., Rational Chebyshev approximations
for the exponential integral
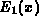 , Math. Comp. 22 (1968),
641--649.
, Math. Comp. 22 (1968),
641--649.
- CT69
-
W. J. Cody and H. C. Thacher, Jr., Chebyshev approximations for the
exponential integral
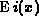 , Math. Comp. 23 (1969), 289--303.
, Math. Comp. 23 (1969), 289--303.
- Gau73
-
W. Gautschi, Algorithm 471. Exponential integrals, Comm. ACM 16
(1973), 761--763.
- Luk69
-
Y. L. Luke, The special functions and their approximations, vol. 2,
Academic Press, New York, 1969.
- Luk76
-
Y. L. Luke, On the expansion of exponential type integrals in series of
Chebyshev polynomials, Theory of Approximation with Applications (A. G.
Law and B. N. Sahney, eds.), Academic Press, Inc., New York, 1976,
pp. 180--199.
- Mos89
-
S. L. B. Moshier, Methods and programs for mathematical functions, Ellis
Horwood Limited, Chichester, 1989, separate diskette.
- Pac70
-
K. A. Paciorek, Algorithm 385. Exponential integral
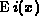 , Comm.
ACM 13 (1970), 446--447, for certification and remarks see same journal
v. 13 (1970), pp. 448--449 and p. 750; v. 15 (1972), p. 1074.
, Comm.
ACM 13 (1970), 446--447, for certification and remarks see same journal
v. 13 (1970), pp. 448--449 and p. 750; v. 15 (1972), p. 1074.
- SZ76
-
I. A. Stegun and R. Zucker, Automatic computing methods for special
functions. Part III. The sine, cosine, exponential integrals, and
related functions, J. Res. Nat. Bur. Standards 80B (1976), 291--311.
- TM68
-
R. F. Tooper and J. Mark, Simplified calculation of
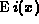 for
positive arguments, and a short table of
for
positive arguments, and a short table of 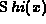 , Math. Comp. 22
(1968), 448--449.
, Math. Comp. 22
(1968), 448--449.
- ULI90
-
Mathematical function library for Microsoft--C, United Laboratories,
Inc., John Wiley & Sons, 1990, includes diskettes. Edition also
exists in Fortran (1989).
- vdLT84
-
C. G. van der Laan and N. M. Temme, Calculation of special functions
: The gamma function, the exponential integrals and error-like functions,
CWI Tract, vol. 10, Centrum voor Wiskunde en Informatica, Amsterdam, 1984.
Abstract:
This document is an excerpt from the current hypertext version of
an article that appeared in Walter Gautschi (ed.),
Mathematics of Computation 1943--1993: A Half-Century of
Computational Mathematics, Proceedings of Symposia in
Applied Mathematics 48, American Mathematical Society,
Providence, RI 02940, 1994.
The symposium was held at the University of British Columbia
August 9--13, 1993, in honor of the fiftieth anniversary of
the journal Mathematics of Computation.
The original abstract follows.
Higher transcendental functions continue to play varied and
important roles in investigations by engineers, mathematicians,
scientists and statisticians.
The purpose of this paper is to assist in locating useful approximations
and software for the numerical generation of these functions, and to
offer some suggestions for future developments in this field.
Applied and Computational Mathematics Division,
National Institute of Standards and Technology,
Gaithersburg, Md 20899
E-mail address: [email protected]
Institute for Physical Science and Technology,
University of Maryland,
College Park, MD 20742
E-mail address: [email protected]
The research of the second author has been supported by NSF
Grant CCR 89-14933.
1991 Mathematics Subject Classification. Primary 65D20;
Secondary 33-00.
Daniel W Lozier
Fri Apr 7 13:50:43 EDT 1995
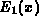 , Math. Comp. 22 (1968),
641--649.
, Math. Comp. 22 (1968),
641--649.
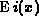 , Math. Comp. 23 (1969), 289--303.
, Math. Comp. 23 (1969), 289--303.
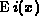 , Comm.
ACM 13 (1970), 446--447, for certification and remarks see same journal
v. 13 (1970), pp. 448--449 and p. 750; v. 15 (1972), p. 1074.
, Comm.
ACM 13 (1970), 446--447, for certification and remarks see same journal
v. 13 (1970), pp. 448--449 and p. 750; v. 15 (1972), p. 1074.
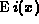 for
positive arguments, and a short table of
for
positive arguments, and a short table of 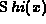 , Math. Comp. 22
(1968), 448--449.
, Math. Comp. 22
(1968), 448--449.