Press
here
to get the full document in PostScript format.
Press
here
to get this subdocument in PostScript format.
Numerical Evaluation of Special Functions
D. W. Lozier and F. W. J. Olver
4.1. Airy Functions
.
This section includes Scorer's functions.
4.1.1. Real Arguments.
Algorithms:
[ Nem71]
,
[ RS81]
.
Software Packages:
[ Pri75, Fortran]
.
Intermediate Libraries:
[ Bak92]
,
[ Mos89]
,
[ ULI90]
.
Comprehensive Libraries:
IMSL,
NAG,
Numerical Recipes,
Scientific Desk,
SLATEC.
Interactive Systems:
Maple.
4.1.2. Complex Arguments.
Software Packages:
[ Amo86, Fortran]
,
[ CJR92, Fortran]
.
Comprehensive Libraries:
NAG,
Scientific Desk,
SLATEC.
Interactive Systems:
Mathematica.
4.1.3. Articles.
[ CCF83]
,
[ Lee80]
,
[ LO93]
,
[ Moo81]
,
[ SAG79]
.
References
- Amo86
-
D. E. Amos, Algorithm 644. A portable package for Bessel functions of
a complex argument and nonnegative order, ACM Trans. Math. Software 12
(1986), 265--273, for remark see same journal v. 16 (1990), p. 404.
- Bak92
-
L. Baker, C mathematical function handbook, McGraw-Hill, Inc., New
York, 1992, includes diskette.
- CCF83
-
J. N. L. Connor, P. R. Curtis, and D. Farrelly, A differential equation
method for the numerical evaluation of the Airy, Pearcey and swallowtail
canonical integrals and their derivatives, Molecular Phys. 48 (1983),
1305--1330.
- CJR92
-
R. M. Corless, D. J. Jeffrey, and H. Rasmussen, Numerical evaluation of
Airy functions with complex arguments, J. Comput. Phys. 99 (1992),
106--114.
- Lee80
-
S.-Y. Lee, The inhomogeneous Airy functions
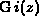 and
and 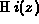 ,
J. Chem. Phys. 72 (1980), 332--336.
,
J. Chem. Phys. 72 (1980), 332--336.
- LO93
-
D. W. Lozier and F. W. J. Olver, Airy and Bessel functions by parallel
integration of ODEs, Proceedings of the Sixth SIAM Conference on
Parallel Processing for Scientific Computing, vol. 2 (R. F. Sincovec, D. E.
Keyes, M. R. Leuze, L. R. Petzold, and D. A. Reed, eds.), Society for
Industrial and Applied Mathematics, Philadelphia, 1993, pp. 531--538.
- Moo81
-
W. Moon, Airy function with complex arguments, Comput. Phys. Comm.
22 (1981), 411--417.
- Mos89
-
S. L. B. Moshier, Methods and programs for mathematical functions, Ellis
Horwood Limited, Chichester, 1989, separate diskette.
- Ném71
-
G. Németh, Chebyshev polynomial expansions of Airy functions, their
zeros, derivatives, first and second integrals, Magyar Tud. Akad. Mat. Fiz.
Oszt. Közl. 20 (1971), 13--33 (Hungarian).
- Pri75
-
P. J. Prince, Algorithm 498. Airy functions using Chebyshev series
approximations, ACM Trans. Math. Software 1 (1975), 372--379.
- RS81
-
M. Razaz and J. L. Schonfelder, Remark on Algorithm 498. Airy
functions using Chebyshev series approximations, ACM Trans. Math. Software
7 (1981), 404--405.
- SAG79
-
Z. Schulten, D. G. M. Anderson, and R. G. Gordon, An algorithm for the
evaluation of the complex Airy functions, J. Comput. Phys. 31
(1979), 60--75.
- ULI90
-
Mathematical function library for Microsoft--C, United Laboratories,
Inc., John Wiley & Sons, 1990, includes diskettes. Edition also
exists in Fortran (1989).
Abstract:
This document is an excerpt from the current hypertext version of
an article that appeared in Walter Gautschi (ed.),
Mathematics of Computation 1943--1993: A Half-Century of
Computational Mathematics, Proceedings of Symposia in
Applied Mathematics 48, American Mathematical Society,
Providence, RI 02940, 1994.
The symposium was held at the University of British Columbia
August 9--13, 1993, in honor of the fiftieth anniversary of
the journal Mathematics of Computation.
The original abstract follows.
Higher transcendental functions continue to play varied and
important roles in investigations by engineers, mathematicians,
scientists and statisticians.
The purpose of this paper is to assist in locating useful approximations
and software for the numerical generation of these functions, and to
offer some suggestions for future developments in this field.
Applied and Computational Mathematics Division,
National Institute of Standards and Technology,
Gaithersburg, Md 20899
E-mail address: [email protected]
Institute for Physical Science and Technology,
University of Maryland,
College Park, MD 20742
E-mail address: [email protected]
The research of the second author has been supported by NSF
Grant CCR 89-14933.
1991 Mathematics Subject Classification. Primary 65D20;
Secondary 33-00.
Daniel W Lozier
Fri Apr 7 13:46:32 EDT 1995
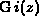 and
and 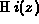 ,
J. Chem. Phys. 72 (1980), 332--336.
,
J. Chem. Phys. 72 (1980), 332--336.
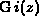 and
and 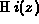 ,
J. Chem. Phys. 72 (1980), 332--336.
,
J. Chem. Phys. 72 (1980), 332--336.