 C Mathematical Function Handbook.
C Mathematical Function Handbook.
Press here to get the full document in PostScript format.
Press here to get this subdocument in PostScript format.
D. W. Lozier and F. W. J. Olver
3.2. Intermediate Libraries .
Under this heading we place software that is in some sense intermediate between software packages, which embody original research contributions, and comprehensive libraries (§ 3.3 below). The libraries we consider here provide support only for mathematical functions. Furthermore, they are largely restricted to codification of existing algorithms with all their advantages---and limitations.
3.2.1.  C Mathematical Function Handbook.
C Mathematical Function Handbook.
This volume with diskette [ Bak92] is keyed to the NBS Handbook of Mathematical Functions [ AS64] . Most chapters of the NBS Handbook have a counterpart here in which brief introductory material is followed by C code listings. A complex arithmetic package is included since C supports only real and integer arithmetic. [ Bak92] advocates the use of C because it ``is rapidly becoming the lingua franca of the computer world'' and ``algorithms written in C should be very portable''. He has written two other books on C programming for technical applications.
3.2.2.  Mathematical Function Library for Microsoft
Fortran or C.
Mathematical Function Library for Microsoft
Fortran or C.
These volumes [ ULI90] exist to ``provide users with a comprehensive set of mathematical function routines to assist them in solving their mathematical problems on IBM PC/XT/AT or compatibles''. Each consists of a looseleaf manual with diskettes. The documentation for each function gives usage instructions, input range, accuracy, definition of the function, algorithm, sample program and sample results. The functions are evaluated only for real arguments. The diskettes contain a compiled library in microprocessor assembly code for use with Microsoft compilers and the Fortran or C source code for use with other compilers.
3.2.3.  Methods and Programs for Mathematical Functions.
Methods and Programs for Mathematical Functions.
This volume with separate diskette of C programs [ Mos89]
presents
a selection of
special functions with real arguments and integer or real parameters.
The programs are designed for double precision, and tables of test
results included for every function typically show absolute or
relative errors (whichever is appropriate) of the order of 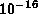 .
Where polynomial or rational approximations are used, the expansion
coefficients were generated in multiple precision using C programs
that are given in the book.
.
Where polynomial or rational approximations are used, the expansion
coefficients were generated in multiple precision using C programs
that are given in the book.
The original abstract follows.
Higher transcendental functions continue to play varied and important roles in investigations by engineers, mathematicians, scientists and statisticians. The purpose of this paper is to assist in locating useful approximations and software for the numerical generation of these functions, and to offer some suggestions for future developments in this field.
Applied and Computational Mathematics Division, National Institute of Standards and Technology, Gaithersburg, Md 20899
E-mail address: dlozier@nist.gov
Institute for Physical Science and Technology, University of Maryland, College Park, MD 20742
E-mail address: olver@bessel.umd.edu
The research of the second author has been supported by NSF Grant CCR 89-14933.
1991 Mathematics Subject Classification. Primary 65D20; Secondary 33-00.