FLOTRAN Basics

FLOTRAN is a finite element analysis program for solving fluid flow and conjugate heat transfer problems.

The governing equations solved by FLOTRAN are the Navier-Stokes equations combined with the continuity equation, the thermal transport equation, and constitutive property relationships.

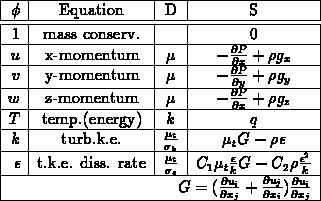
This equation represents a number of fluid flow equations:

Turbulent Model

As the Reynolds number increases, the flow becomes unstable and start to form eddies. This flow phenomenon is characterized as turbulent flow. The forming and disappearing of eddies change instantaneously and randomly in small scale. It would require very small time steps and very fine meshes to model the full time-dependent, small scale vortices of the Navier-Stokes equations. FLOTRAN uses the model to approximate the turbulent flow.

The model uses time-averaging to obtain fluid flow equations. The velocity is expressed in terms of a mean velocity and a fluctuating velocity.

Integrate over a small time scale:

Rewrite the compressible Navier-Stokes euqations in tensor form:

Perform time-averaging integration on above equation over the small time scale:

The time-averaged Navier-Stokes equations becomes:

are the time-averaged mean velocities. Additional advection terms are Reynolds stresses:

Introduce turbulent viscosity and define the effective viscosity :

Turbulent Navier-Stokes euqations in tensor form:

Spalding and Launder Model

Turbulent kinetic energy

Turbulent kinetic energy dissipation rate

Length scale related to turbulent kinetic energy

Turbulent viscosity

The source terms include the pressure gradient and the buoyancy forces and can also include additional source terms such as distributed resistances (head loss factors, friction factors, or permeability).

The density may be taken to be a function of temperature and/or pressure.. Several different polynomial relationships are available. Coefficients are calculated based on a user-selected set of data points.

For cases at high Reynolds number a two-equation turbulence model is used. In the turbulent case the effects of the time-varying velocity fluctuations are accounted for by an eddy viscosity model. Turbulent viscosity and turbulent thermal conductivity components are calculated based on the turbulent kinetic energy and turbulent kinetic energy dissipation rate and added to the corresponding laminar properties. The solution of partial differential equations based on the conservation of momentum provide the values of and . The result is a spatially varying effective viscosity and effective conductivity field.

The governing equations are solved in sequential fashion using a segregated velocity-pressure solution algorithm. The process features the development of a Poisson-like pressure equation based on conservation of mass. An approximate solution to the momentum equations provides the forcing function for the pressure equation and the resulting pressure field is used to update velocity to ensure conservation of mass. This method features equal order elements for pressure and velocity and so all dependent variables are obtained for the same set of finite element nodes.

A monotone streamline upwind method is used to handle the nonlinear advection terms in the governing transport equations. The velocity field existing at any point in the solution process is used to identify which node(s) in a given element are downwind nodes. Streamlines from this velocity field are traced from the downwind nodes upstream to see where they entered the element. The advection term for that element is then calculated using conditions at that location. This method provides a stable solution while minimizing numerical diffusion, an important consideration in any approach to a mixing problem.

FLOTRAN Features

Steady-State or Transient Solution Algorithm
Equal Order Approximation for Velocity and Pressure
1. No staggered grids
2. No mixed order interpolation
Monotone Streamline Upwind Appproximation for Advection Terms
1. Increased accuracy over conventional upwind
2. Stable at high Reynolds numbers
Minimal Execution Time Requirements
1. Segregated sequential solution
2. Iterative solution methods
Minimal Storage Requirements
1. Bandwidth independent
2. In-core solution method

FLOTRAN Capabilities

2-D or 3-D Geometries
Axisymmetric Geometries
Laminar or Turbulent Flow and/or Heat Transfer
Forced, Free, or Mixed Convection
Conduction
Conjugate Heat Transfer
Distributed Flow Resistances
Porous Media
Incompressible or Compressible Flow
Steady State or Transient
Total Energy Equation
Global Convergence Status

Boundary Conditions:
1. Prescribed Nodal Values - Velocity, Pressure, Temperature,Turbulent Kinetic Energy, Turbulent Energy Dissipation.
2. Prescribed Heat Flux
3. Prescribed Heat Source
4. Prescribed Film Coefficient
5. Adiabatic
6. Symmetry
7. Periodic Boundaries

Getting Started Using FLOTRAN

FLOTRAN has been integrated with ANSYS. This integration allows users to build the finite element models using ANSYS PREP7 and to pass the model data to flotran for the various analyses. Once the FLOTRAN analyses are done, the data can then be transferred to the ANSYS postprocessor, POST1.

IDEAS and PATRAN can also be used to pre- and postprocess finite element models for FLOTRAN analyses.

In this course, we will use only ANSYS for pre- and postprocesses.

FLOTRAN Processes

Preprocessing (or model generation and B.C./I.C.) - ANSYS,
Solution - FLOTRAN,
Postprocessing (or results evaluation) - ANSYS.

FLOTRAN Modeling

Only two element types are valid for FLOTRAN analyses. FLOTRAN uses the MAT element attribute to distinguish fluid elements from solid elements. Fluid elements must have MAT = 1, and solid elements elements are identified by MAT > 1. The REAL ATTRIBUTE is to flag elements with distributed resistance.

Modeling Constraints

Element Types
1. Quad and triangles (2D) - PLANE55
2. Hex and tet (3D) - SOLID70
Element Material Number
1. MAT = 1 - Fluid Elements
2. MAT > 1 - Solid Elements
Cartesian Coordinates
Rotating Coordinates
Cylindrical Coordinates

Modeling Guidelines

Examine the solution domain for possible symmetries
Sketch the geometry for planning the geometry model and the finite element model
Anticipate the analysis requirements
1. Regions of high gradients in the solution variables. These regions usually require finer meshes.
2. Important Boundaries such as flow inlets, flow exits, heated areas, and constant temperature boundaries.
3. Mesh size requirements to be considered with maximum limit of nodes and CPU and storage requirements.
Sketch the proposed mesh
Construct the geometry and elments with top-down or bottom-up technique

Boundary Condition Types

Symmetry boundaries
- Geometry half symmetry or Mirror image
- Align with a coordinate axis
- Zero normal velocity on the bounaries
Inflow boundaries - specify either inlet velocity or pressure
Outflow boubdaries - specify pressure only
Wall boundaries - zero flow velocity on the wall
Periodic Boundaries - corresponding boundaries with identical flows
Thermal boundary conditions - do not affect flow boundary conditions
Initial conditions - specified with separate boundary condition in each LOAD STEP(ANSYS)

Optimum Order for Setting Boundary conditions

Symmetry boundaries
Inflow boundaries
Outflow boundaries
Wall boundaries

When a boundary condition is repeatedly specified, the latter overwrite the former one. Unspecified flow boundaries are treated as natural boundary conditions where mass can enter or leave the boundaries.

FLOTRAN Modeling - Example 1

   /TITLE,Flow through a Curved Channel 
   /UNITS,SI  ! SI units  
   /PREP7     ! Begin PREP7 preprocessing 
   ET,1,55    ! Plane55 Element type 
   ! Define pipe dimensions 
   D=20   ! channel width 
   R=0.5*D 
   RI=40  ! Radius of curved center line of channel 
   D4=D*4 ! Four times half channel width 
   RR=R*R 
   V0=200 
   K,1,,-R 
   K,2,,R 
   K,3 
   L,1,2    
   /pnum,line,1 
   /pnum,kp,1   
   /pnum,area,1 
   /pnum,node,1 
   lplot   
   LESIZE,1,,,16,-4 
   ESHAPE,2 ! Quadrilaterals only 
   /triad,off  ! turn off coordinate traid at origin 
   KPLOT    
   K,4,D4+RI  
   K,5,D4+RI,D4*2+RI  
   L,3,4    
   L,4,5    
   LFILL,2,3,RI 
   LESIZE,2,,,32,0.5 
   LESIZE,3,,,48,2.5 
   LESIZE,4,,,32 
   LPLOT 
   ADRAG,1,,,,,,2,4,3 
   APLOT    
   AMESH,ALL
   /pnum,node,0 
   /pnum,kp,0  
   /pnum,elem,0 
   /triad,on  
   EPLOT 
   DOF,VX,VY,VZ,PRES,ENKE,ENDS 
   FLDA,1S,JB,cflow 
   FLDA,1S,IT,100   
   FLDA,1S,RS,T  
   FLDA,1S,TB,T  
   NSEL,s,loc,x  
   NPLOT   
   /pbc,all,,a  
   D,all,vy   
   GET,NMAX,NODE,,NUM,MAX 
   DO,I,1,NMAX 
    RSQ=NX(I)**2+NY(I)**2 
    VZ0=V0*(1.0-(RSQ/RR)**2) 
    D,I,VX,VZ0 
   ENDDO 
   nsel,s,loc,y,RI+D4*2   
   d,all,pres   
   LSEL,S,LINE,,6,7 
   LSEL,A,LINE,,9,10 
   LSEL,A,LINE,,12,13 
   NSLL,S,1 
   D,ALL,VX,,,,,VY 
   lsel,all 
   NSEL,ALL 
   FLDA,2P,D0,9.98E-1   
   FLDA,2P,V0,0.01  
   FLDA,2P,C0,6.04E-3   
   FLDA,2P,CP,4.199 
   FLDA,2S,NP,1.01325E6 
   FLWRITE,ALL 
   FINISH  
   /EXIT

FLOTRAN Modeling - Example 2

   /TITLE,Flow through a Curved Pipe  
   /UNITS,SI     
   /PREP7    
   ET,1,55  
   ET,2,70  
   ! Define pipe dimensions  
   D=20    ! Pipe diameter  
   RI=40   ! Radius of curved center line of pipe   
   D4=D*4  ! Four times diameter length  
   RR=(0.5*D)**2  
   V0=200  
   PCIRC,0.4*D,,0,90     
   PCIRC,0.4*D,0.5*D,0,90     
   NUMMRG,ALL  
   /PNUM,line,1  
   /PNUM,area,1  
   /PNUM,kp,1    
   LPLOT     
   TYPE,1  
   LESIZE,1,,,8  
   LESIZE,2,,,8,2  
   LESIZE,3,,,8,0.5  
   LESIZE,5,,,4,2  
   LESIZE,7,,,4,2  
   APLOT  
   ESHAPE,2  
   AMESH,ALL     
   ARSYM,X,ALL   
   NUMMRG,ALL  
   ARSYM,Y,ALL   
   NUMMRG,ALL  
   NUMCMP,NODE
   /pnum,node,1  
   /triad,off    
   TYPE,2  
   K,23,,,D4+RI    
   K,24,D4*2+RI,,D4+RI    
   L,3,23  
   L,23,24  
   lplot     
   LFILL,13,16,RI  
   LESIZE,13,,,16,0.25  
   LESIZE,18,,,32  
   LESIZE,16,,,24,5  
   /VIEW,1,1,1  
   VDRAG,ALL,,,,,,13,18,16  
   NUMMRG,NODE  
   ASEL,S,TYPE,,1  
   ACLEAR,ALL  
   /pnum,node,0  
   /pnum,kp,0    
   /pnum,elem,0  
   /triad,on     
   EPLOT  
   VSEL,S,TYPE,,2    
   NSLV,S,1  
   DOF,VX,VY,VZ,PRES,ENKE,ENDS   
   NSEL,S,LOC,Z  
   NPLOT
   /pbc,all,,a   
   D,ALL,VX  ! Flow at inlet  
   D,ALL,VY  
   GET,NMAX,NODE,,NUM,MAX  
   DO,I,1,NMAX  
    RSQ=NX(I)**2+NY(I)**2  
    VZ0=V0*(1.0-(RSQ/RR)**2)  
    D,I,VZ,VZ0  
   ENDDO  
   NSEL,S,LOC,X,RI+D4*2  
   NPLOT  
   D,ALL,PRESS  ! Pressure at outlat  
   ASEL,S,EXT  ! Select external walls  
   ASEL,U,AREA,,1,8  ! Exclude inlet  
   ASEL,U,LOC,X,RI+D4*2  ! Exclude outlet  
   NSLA,S,0  ! Select all nodes on the walls  
   D,ALL,VX,,,,Vy,VZ  ! No slip on walls  
   ASEL,ALL  
   NSEL,ALL  
   ESEL,S,type,,2  
   FLDA,1S,JB,cpipe  
   FLDA,1S,IT,50  
   FLDA,1S,RS,T  
   FLDA,1S,TB,T  
   FLDA,2S,NP,1.01325E6  
   FLDA,2P,D0,9.98E-1  
   FLDA,2P,V0,0.01  
   FLDA,2P,C0,6.04E-3  
   FLDA,2P,CP,4.199  
   FLWRITE,ALL  
   SAVE

FLOTRAN Setup

ANSYS incorporates FLOTRAN menus to setup FLOTRAN analysis control parameters within PREP7. The control data, the model geometry, the boundary conditions, and initial conditions are then written into separate FLOTRAN files for FLOTRAN to use.

FLOTRAN files for a particular problem use a common file name (jobname) with different extensions to identify the types of file. The jobname must be consistent with the file naming convention and is limited to 8 characters. If a jobname consists of digits as the trailing charaters, the digits are treat as a case identifier and will be stripped from the jobname.

  jobname.xgm    transfer geometry file written by ANSYS PREP7  
  jobname&.xbc   transfer B.C. file written by ANSYS PREP7  
  jobname.geom   FLOTRAN translated geometry file  
  jobname&.bc    FLOTRAN boundary condition file  
  jobname&.run   FLOTRAN run control file  
  jobname&.res   FLOTRAN results file  
  jobname&.rso   FLOTRAN backup results file  
  jobname&.rsw   FLOTRAN wall file  
  jobname&.prt   FLOTRAN print file    

  Transient Runs
  jobname&.xic   transfer initial condition file  
  jobname&.ic    FLOTRAN initial condition file  
  jobname&.#     FLOTRAN intermediate transient results file #

FLOTRAN Screens

   <1S>   Basic Run Data  
   <2S>   Properties      
   <2P>   User Fluid Data  
   <3S>   Turbulence       
   <4S>   Relaxation Parameters   
   <5S>   Solution Control   
   <6S>   Transient Control   
   <7S>   Rotational Terms    

      Quit, No Changes  
      Write File and Exit    

   ENTER CODE AND VALUE (e.g.  IT 100)

Screen 1S - Basic Run Data

   Create Post File          F   Flow Termination         0.0E+00   
   Iterations                50  Energy Termination      0.0E+00   
   Output Frequency          5   Print U Velocity         F   
   Restart                   F   Print V Velocity         F   
   Batch Output              F   Print WVelocity          F   
   Flow Analysis             T   Print Pressure           F   
   Turbulent                 T   Print Temperature        F   
   Compressible Solution     F   Print Turb Kin Energy    F   
   Thermal Analysis          F   Swirling Flow            F   
   Print Turb Dissipation    F   Output Residuals         F

Screen 2S - Properties

   Fluid                    CONSTANT  
   Reference Pressure       1.0133E+6  
   Nominal Temperature      2.9300E+2  
   Ambient Temperature      2.9300E+2  
   Stagnation Temperature   2.9300E+2  
   Print Density            F  
   Print Viscosity          F  
   Print Conductivity       F    
   X Acceleration            0.000E+00  
   Y Acceleration           0.000E+00  
   Z Acceleration           0.000E+00  
   Variable Density         F  
   Variable Viscosity       F  
   Variable Conductivity    F  
   Property Update Freq.    1

Screen 2P - User Fluid Data

           (Fluid CONSTANT, LIQUID or GAS only)   

                        Base  
                        Value              Coeff  
   Density          9.9800E-1      0.0000E+0  
	                               0.0000E+0
	                               0.0000E+0  
   Viscosity        1.0000E-2      0.0000E+0  
	                               0.0000E+0
	                               0.0000E+0  
   Conductivity     6.0400E-3      0.0000E+0  
	                               0.0000E+0
	                               0.0000E+0  
   Specific Heat    4.1990E+0  
   Ratio CP/CV      1.4000E+0

Variable Properties

Functional Form for Gas

Density: Ideal Gas Equation ( )

Viscosity: Sutherland's Formula

Conductivity: Sutherland's Formula

Functional Form for Liquid

Density: Quadratic Polynomial

Viscosity: Exponential

Conductivity: Exponential

Screen 3S - Turbulence Parameters

  Inlet Intensity      0.0100     Print Eff Viscosity       F  
  Inlet Scale Factor   0.0100     Print Eff Conductivity    F  
  Turbulence Ratio     1.0E+03  
                                      Schmidt Number  
  Temperature          1.0000     Turb Kinetic Energy       1.0000  
                                      Turb Dissipation Rate     1.3000 

                          Turbulence Parameters
  CMu    0.0900     Kappa    0.4000     E    9.000  
  C1     1.4400     C2       1.9200     A    26.00

Screen 4S - Relaxation Parameters

  U Velocity Relaxation       0.500  
  V Velocity Relaxation       0.500  
  W Velocity Relaxation       0.500  
  Pressure Relaxation         0.500  
  Turb Kin Energy Relax       0.500  
  Turb Dissipation Relax      0.500    
  Temperature Relaxation      0.500  
  Density Relaxation          0.500  
  Viscosity Relaxation        0.500  
  Conductivity Relaxation     0.500   
  Eff Viscosity Relax         0.500  
  Eff Conductivity Relax      0.500    
  
  Momentum Inertia            1.E+15  
  Pressure Inertia            1.E+15  
  Turbulence Inertia          1.E+15    
  
  Artificial Viscosity        0.E+00

Screen 5S - Solution Control

	                        Pressure       Energy    
  Semi-direct Solution      T          F  
  Convergence Criteria      1.E-07     1.E-05  
  Maximum Iterations        300        300 

	              TDMA Iterations
  Momentum              1      Kinetic Energy          10  
  Pressure              100    Dissipation Rate        10  
  Temperature           25  
                              [VM=1,P=2,K=3,E=4,T=5,  Rho=6]  
  Debug Print Level     0      Solution Error Est.      0

Screen 6S - Transient Control

  Transient Solution         F  
  Number of time steps       10   
  Time step                  -1.0000E+0   
  Stop Time                  1.0000E+0   
  Output Time Increment      1.000E+09   
  Output Step Increment      9999

Screen 7S - Rotational Terms

  X Omega (Rot. speed)      0.000E+00  
  Y Omega (Rot. speed)      0.000E+00  
  Z Omega (Rot. speed)      0.000E+00    
  X Rotat. Axis Offset      0.000E+00  
  Y Rotat. Axis Offset      0.000E+00  
  Z Rotat. Axis Offset      0.000E+00

Running FLOTRAN

Once the finite element model has been prepared by ANSYS PREP7, (IDEASS or PATRAN,) you may submit it to FLOTRAN by entering:

flotran

and respond to the prompts.

FLOTRAN Production Dynamic

Version 2.1a Convex 6/01/93

This is the FLOTRAN (R) general purpose finite element computer program for fluid flow and heat transfer analysis. Neither Swanson Analysis Systems, Inc. nor any distributor supplying this program assume any responsibility for the validity, accuracy, or applicability of any results obtained from the FLOTRAN (R) program. Users must verify their own results.

1. Setup Run 2. Submit Run 3. Results Processing 4. Utilities 5. Exit
1

1. Geometry 2. Boundary Cond. 3. Initial Cond. 4. Run File 5. Exit
1

Enter FLOTRAN jobname (8 characters)
cflow

Translate geometry for cflow ? (Y or N)
y

Overwrite current geometry? (Y or N)
y

Enter preprocessor file name

Translate BC for cflow ? (Y or N)
y

Enter preprocessor file name

1. Setup Run 2. Submit Run 3. Results Processing 4. Utilities 5. Exit
5

Do not select "2. Submit Run" for running a batch job. Exit flotran and use the NIST modified FLORUN command to submit a FLOTRAN batch job:

florun.nist <jobname> batch [CPU hours] [Mem-size Mb]

FLOTRAN Solution

A complete pass through all the equations is called a global iteration consisting of

Approximate solution of each momentum equation in sequential fasion.
Solution of the pressure equation.
Calculation of velocities to conserve mass.
Solution of the energy equation.
Update of the laminar properties.
Solution of the turbulence equations.
Update of the turbulent properties.

The progress of the solution is monitored by observing the rate of change of the solution from one global iteration to the next. The analyst can restart the analysis until satisfied that the rate of change of the solution is small enough.

The approximate solution of the momentum equation is obtained through the use of a tri-diagonal matrix algorithm. The momentum equations are relaxed to provide a stable solution.

The pressure equation is solved with a pre-conditioned conjugate gradient routine. An incomplete Choleski decomposition provides the preconditioning. The approach is particularly well suited for practical applications because the solver requires very little storage other than those associated with the non-zero matrix terms in the nonsymmetric momentum equation. The performance of the method is bandwidth independent and it is ideally suited towards use with irregular and unstructured finite element grids.

Convergence Monitoring

ITER   U-MOM       V-MOM       PRESS       ENERG       K           EPSILON  
   1   0.000E+00   0.000E+00   1.000E+00   0.000E+00   0.000E+00   0.000E+00  
   2   4.823E-02   4.731E-02   2.142E+00   0.000E+00   9.991E-01   6.062E-01  
   3   1.563E-02   1.633E-02   7.292E-01   0.000E+00   3.453E-01   3.430E-01  
   4   1.368E-02   1.582E-02   3.680E-01   0.000E+00   2.090E-01   2.421E-01  
   5   1.316E-02   1.520E-02   2.053E-01   0.000E+00   1.517E-01   1.907E-01  
   6   1.276E-02   1.487E-02   1.605E-01   0.000E+00   1.214E-01   1.587E-01  
   7   1.231E-02   1.463E-02   1.199E-01   0.000E+00   1.031E-01   1.370E-01  
   8   1.184E-02   1.421E-02   7.186E-02   0.000E+00   9.050E-02   1.215E-01  
   9   1.134E-02   1.423E-02   9.942E-02   0.000E+00   7.999E-02   1.073E-01  
  10   1.095E-02   1.385E-02   5.649E-02   0.000E+00   7.142E-02   9.527E-02      


                    Global Convergence Statistics

       U-MOM       V-MOM       PRESS       ENERG       K           EPSILON  
 Err   3.978E+03   4.579E+03   3.483E+06   0.000E+00   1.805E+08   1.130E+06  
 Sig   6.750E+03   8.080E+03   6.349E+06   0.000E+00   5.080E+08   1.476E+06


 Total Mass Flow In    =   6356.2  
 Total Mass Flow Out   =   -6356.0    


 Total Energy Flow In  =   0.78201E+07  
 Total Energy Flow Out =   -0.78198E+07

Results Evaluation

Field Variable Information
1. Velocity
2. Pressure
3. Temperature
4. Total Temperature
5. Turbulent Kinetic Energy
6. Turbulent Dissipation Rate
7. Density
8. Molecular Viscosity
9. Effective Viscosity
10. Thermal Conductivity
Calculated Field Quanities
1. Stream Function (2D)
2. Velocity Magnitude (3D)
3. Wall Film Coefficients
4. Wall Heat Fluxes
5. Pressure Coefficient
6. Mach Number
7. Total Pressure
8. Nodal Heat Fluxes
9. Nodal Film Coefficients
Solution Reliability Statistics
1. Nodal Residuals
2. Nodal Error Indicators
Graphic Output:
1. All of the imaging capabilities (e.g., contour plots, vector plots, etc.) All FLOTRAN variables can be used for postprocessing.
2. Massless Particle Tracking is available in the ANSYS and IDEAS programs.

Post Processing Variables

   VX     X direction Velocity  
   VY     Y direction Velocity  
   VZ     Z direction Velocity  
   PRES   Pressure  
   TEMP   Temperature  
   ENKE   Turbulent Kinetic Energy  
   ENDS   K. E. Dissipation Rate  
   NDEN   Nensity  
   NVIS   Viscosity  
   TCON   Fluid Thermal Conductivity  
   EVIS   Effective Viscosity  
   ECON   Effective Conductivity  
   TTOT   Total Temperature  
   STRM   Stream Function  
   PCOE   Pressure Coefficient  
   MACH   Mach Number  
   PTOT   Total Pressure  
   HFLX   Heat Flux  
   HFLM   Film Coefficient

FLOTRAN Postprocessing

The FLOTRAN results file, <jobname&.res> is a unformatted binary file that can be read by the FLREAD command in ANSYS postprocessing.

Read Results File:

FLREAD, jobname, ext

Where ext is the extension of FLOTRAN filename.

   res   Nodal results file for all degrees of freedom as well as properties  
   nqh   Heat flux and filem coefficients  
   eid   Error indicator file

Plot Results:

   PLNSOL, variable (Velocity, Temperature, Pressure, etc.)

Plot velocity vectors:

   PLVECT, V

Plot graphs along a line path:

   Define Path:
     LPTATH,node1,node2,....node10
   Define Name of Graph:
     PDEF, User-define-name, Variable
   Produce Graph:
     PLPATH, User-define-name

Integrate Pressures:

   INTSRF, PRES

Particles Tracing:

   Define up to 50 points in problem domain
      TRPOIN,x,y,z 
      TRPOIN,PICK 
      List existing points with TRPLIS
      Delete points with TRPDEL
      
   Execute particle tracing of any post processing variable
      PLTRAC, FLUID, item, compon

3D Contour Plots:

      /CTYPE,1
      /EDGE,off
      ASEL,S,EXT
      NSLA,S,ALL,1
      NSEL,INVE
      PLNSOL,V,SUM

3D Cross Section Contour Plots

      /TYPE,3,SECT
      /FOCUS,3,RI,0,D4+RI
      /VIEW,3,1,0,0
      NSEL,s,loc,x,RI
      ESLN,,0
      PLNSOL,V,SUM
      PLNSOL,PRESS

Transient results files use ANSYS POST26.

FLOTRAN Postprocessing Example

  RESUME,cpipe,db   
  /POST1    
  FLREAD,cpipe,res  
  /WINDOW,1,FULL    
  /WINDOW,2,-.2,.4,-1,-.4  
  /WINDOW,3,.4,1,-1,-.4  
  /TLABEL,0.25,-.98,Z=D*4  
  /TLABEL,1,-.98,X=RI  
  /window,all,off   
  /CTYPE,1  
  nsel,s,loc,y,-99,0    
  esln,,0  
  /window,1,on  
  /VIEW,1,0.5,1,-0.5  
  PLNSOL,V,SUM  
  /noerase  
  /window,1,off  
  NSEL,ALL  
  /CTYPE  
  /window,2,on  
  /TYPE,2,SECT  
  /FOCUS,2,0,0,D4  
  /VIEW,2,0,0,1  
  nsel,s,loc,z,D4  
  esln,,0  
  PLNSOL,V,SUM  
  /window,2,off     
  /window,3,on  
  /TYPE,3,SECT  
  /FOCUS,3,RI,0,D4+RI  
  /VIEW,3,1,0,0  
  nsel,s,loc,x,RI  
  esln,,0  
  PLNSOL,V,SUM

Error and Trouble Shooting

FLOTRAN error message indicates a fatal error. FLOTRAN performs a number of data checks to ensure that the problem posted is valid. There are, of course, many inputs that cannot be verified; users must verify them. Diverging solution, and unexpected results are often caused by invalid input.

Common Causes of Divergence

Incorrect problem setup
- Highly skewed or tapered finite elements
- Missing or duplicate nodes
- Incorrect or missing boundary conditions
- Unreferenced nodes
- Poorly defined problem domain
Incorrect problem setup in FLOTRAN
- Inconsistent property information
- Invalid control parameters
Tough fluids problem

Trouble Shooting Guide

Users may check the boundary conditions by setting both Flow and Thermal in Screen 1S to F(false) and Iteration to 0. The FLOTRAN will generate a jobname.prt that tabulates the mass flows at all inlets and outlets. If unexpected inlets/outlets are listed, eliminate them.
Make sure information on Screen 2S and Screen 2P are realistic and consistent. For example, a temperature data given in when it should be given in may give an unrealistic density and cause divergence.
If the divergence occurs on the first few iterations, it is usually either a modeling error or an incorrect FLOTRAN data specification. If a FLOTRAN analysis runs for a short time (5-10 iterations) where it appears to converge and then diverges, it may be caused by improper run parameters. For example, a laminar flow analysis on a high Reynold number situation may first converge then diverge.
Reducing the relaxation parameters on Screen 4S may help the convergence. These parameters are set at 0.5 and may be reduced to 0.2-0.3 to better control the convergence. Another alternative is to lower the inertia number on Screen 4S.
If these methods stiil fail to converge, it may be possible to pre-condition the problem. This is done by raising the viscosity an appropiate order of magnitude to obtain a laminar solution and then introducing the turbulence.

FLOTRAN Applications

FLOTRAN has been applied to a variety of applications from a wide range of industries.

AUTOMOTIVE
1. Study of air flow over vehicles
2. Passenger compartment flow
3. Fluid flow, conjugate heat transfer analysis of engine exhaust manifolds and water jackets - Flow through radiator passages
4. Flow analysis through various valve configurations
AEROSPACE
1. External flow over various wing configurations
2. Internal flow analyses of nozzels and ducts
3. Fluid flow, heat transfer analysis of aircraft passenger compartments
4. Compressible flow analysis with shock/boundary layer interaction
5. Thermal analyses
ELECTRONICS
1. Electronic cooling in a computer terminal
2. Conjugate heat transfer analysis of IC package
3. Heat transfer analysis of electronic fin array
4. Heat transfer analysis of a simulated card cage
5. Disk flow
POWER
1. Thermally stratified turbulent pipe flow
2. Pressurized thermal shock
3. Natural convection cooling
4. Fluid bed reactor analysis
5. Valve analysis
HVAC
1. Flow inside buildings
2. Flow in ducts
3. Flow in pipes
4. Flow through coolant passages
5. Heat exchanger analysis
TURBO MACHINERY
1. Torque converter flow analysis
2. Flow through vaned and vaneless diffusers
3. Labyrinth seal flow
4. Blade cooling analysis
5. Flow in pump, compressor, turbine, impeller passages

Hai Tang, last updated December 15, 1995