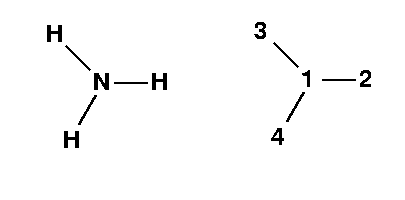
NH3
is a neutral molecule and has 10 (7+1+1+1) electrons. It has an even number of electrons, and according to the Pauli principle they are all paired up and it is a ground state singlet. Therefore the charge/multiplicity entry is 0 1. The molecule itself looks like:


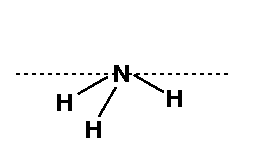
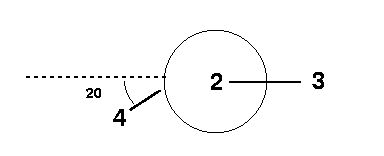
From the Hint, you were told that you should draw a Newman projection of the 4-1-2-3 connectivity in order to determine the dihedral angle. You can see from the figure that the value of the dihedral angle = 200°.
The complete input file for this molecule is:
#P HF STO-3G OPT
NH3 OPTIMIZED GEOMETRY at STO-3G
0 1
N1
H2 1 RNH
H3 1 RNH 2 HNH
H4 1 RNH 2 HNH 3 DA
RNH 1.0
HNH 120.0
DA 200.0
(CH3)2CO is a neutral molecule and has 32 (2*(6+3)+6+8) electrons. Therefore the charge/multiplicity entry is
0 1.
The complete input for Z-matrix format for this molecule is:
#P RHF/STO-3G Opt Test
(CH3)2CO: acetone Geometry Optimization
0 1
C1
O2 1 RCO
C3 1 RCC 2 120.0
C4 1 RCC 2 120.0 3 180.0
H5 3 RCH 1 109.0 2 90.0
H6 3 RCH 1 109.0 2 210.0
H7 3 RCH 1 109.0 2 -30.0
H8 4 RCH 1 109.0 2 90.0
H9 4 RCH 1 109.0 2 210.0
H10 4 RCH 1 109.0 2 -30.0
RCH 1.08
RCO 1.20
RCC 1.30
Li-C5H5 is neutral and has 38 (3+5*(6+1)) electrons. Therefore, the charge/multiplicity entry is 0 1.
The molecule looks like this:
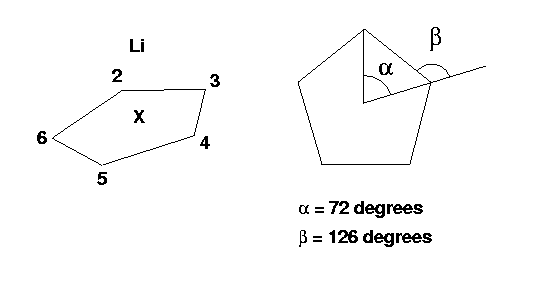
The complete input file for this molecule in Z-matrix format is:
#P HF 6-31G(d) OPT-z-matrix
Li-C5H5 OPTIMIZED GEOMETRY at 6-31G(d)
0 1
X
C2 1 rxc
C3 1 rxc 2 72.0
C4 1 rxc 3 72.0 2 180.0
C5 1 rxc 4 72.0 3 180.0
C6 1 rxc 5 72.0 4 180.0
H2 2 rch 3 126.0 1 180.0
H3 3 rch 4 126.0 1 180.0
H4 4 rch 5 126.0 1 180.0
H5 5 rch 6 126.0 1 180.0
H6 6 rch 7 126.0 1 180.0
Li 1 rlix 2 90.0 3 90.0
rxc 1.20
rch 1.08
rlix 1.40