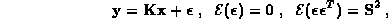
Since first kind integral equations are ubiquitous in measurement processes, they are of great interest to NIST and ACMD. Discretizations of such equations give
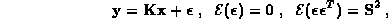
where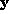 
is a vector of measurements, 
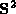is the
covariance matrix for 
,
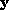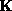is a known instrument response matrix, and
is a vector to be determined.
This problem is usually poorly conditioned, with a wildly
oscillating, unphysical solution.
Previous efforts have produced the algorithm BRAKET-LS which stabilizes
the solution by requiring nonnegativity and computes confidence interval bounds
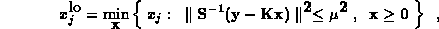
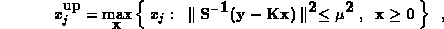
where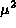 
determines the confidence level.
The method requires initial estimates which do not have to bracket the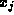 
very closely, but the computational effort is greatly reduced if they do.
More recent efforts have been devoted to generating such estimates and to
developing diagnostic tests for the residuals generated by the corresponding
solutions. The unfolding codes FERDO and FERD have been adapted to create
subroutines which calculate good suboptimal initial intervals. FERDO uses a
regularization technique which requires the solution to be in the intersection
of the measurement uncertainty ellipsoid with a guaranteed ellipsoid derived
from the nonnegativity constraints. The suboptimal intervals are based on a
convex combination of the two, and the widths of the intervals depend on the
choice of the regularization parameter. FERD is based on the duals of the
above problems. In the dual for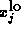 
the primal constraints are
replaced by lower bias inequalities and for 
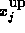by upper bias
inequalities. Beginning with initial estimates which are neither lower nor
upper biased, FERD implements an elimination iteration to find feasible
solutions which are used as starting estimates for BRAKET-LS. Another
algorithm, called OPTIMO, replaces the measurement constraint ellipsoid with a
circumscribing box and uses linear programming to generate suboptimal initial
intervals. Preliminary tests have yielded good results for smaller problems
but failures because of excessive iterations for problems with more than 60
unknowns. New diagnostic tests for all of these methods were obtained by
applying time-series methods to the residuals. Future efforts will be devoted
to further developments of the OPTIMO algorithm, fine tuning of the FERDO and
FERD algorithms, further development of residual diagnostic tests, and
documenting the whole package.