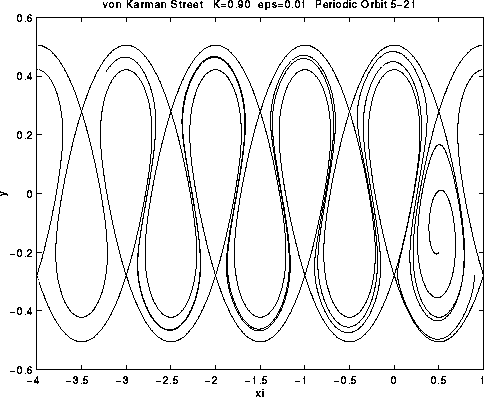
The understanding of a number of important natural phenomena, as well as the development of many technological applications, is based on an analysis of the dynamics of small particles, such as bubbles, drops, and solid particles, in fluid flows. At low concentrations, particle interactions are negligible, and if the particles are sufficiently small, the dominant fluid force on a particle is simply a Stokes drag force. The scale of this drag force is indicated by a dimensionless ratio called the Stokes number. In a number of important applications, the Stokes number is very small, which implies that inertial effects are small, and this has the effect of making the equations describing the particle motion stiff, in the sense that the time scale associated with particle inertia is much smaller than the time scale associated with the background fluid flow. Practically speaking, this stiffness makes accurate numerical simulation of the motion of many particles expensive in terms of computer time. Furthermore, a particle typically has more than one degree of freedom, which means that the position-velocity phase space of such a model is at least four dimensional, making visualization of the results of simulations difficult. In work completed this year, a model of the dynamics of small, rigid, dilute spherical particles in the wake of a bluff body, modeled as a two-dimensional Kármán vortex street, was analyzed using methods of nonlinear dynamics, in order to study an unexpected effect observed in experiments called particle focusing. Using geometric singular perturbation theory, it was shown that the motion of an aerosol particle, which takes place in the four-dimensional position-velocity phase space of the model, rapidly approaches a motion on a two-dimensional center manifold. Thus, what started out as a stiff initial-value problem for a set of four ordinary differential equations has been reduced to a nonstiff initial-value problem for only two ordinary differential equations. Numerical simulations of this reduced problem indicate there is a stable periodic attractor in the model, which provides an explanation for the observed particle focusing (see illustration below). In work currently in progress, the effects of gravity on the model are being analyzed. This collaboration will be completed upon publication of a paper documenting this work.

Caption: {Particle trajectories in the reduced model corresponding to two different shown are the separatrices which define the channel in the unperturbed case.