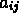Isabel Beichl, ACMD
Francis Sullivan, Supercomputing Research Center
The permanent of an nxn matrix with entries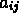 
is
defined by
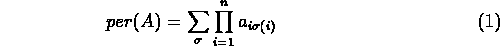
where the sum is over all permutations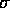 
of 
.
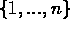Informally, it similar to the determinant but without the
alternating signs. However, in contrast with the determinant,
no efficient procedure for computing this function is known.
The permanent is important because it is equivalent to counting
perfect matchings of a bipartite graph and arises naturally in
a number of fields including
discrete optimization, statistical physics and
scheduling.
Computing the permanent is typical of the kind of combinatorial
problems that arise in data communications, a class of issues
that NIST will need to face in coming years.
Based on our experience in Monte Carlo simulation
and in linear algebra we have developed an approximation
algorithm that extends the best approximation algorithm
for computing the permanent (Jerrum & Sinclair, SIAM J. Comput. v. 18)
to a wider class of matrices.
We use importance sampling
as a method for reducing the variance of the samples generated
and thus
hasten convergence. We are in the process of developing
a particularly efficient implementation based on some little
known methods of linear algebra.