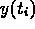Bert W. Rust and Dianne P. O'Leary, ACMD
Many measured distributions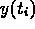 
are modeled by
a system of integral equations
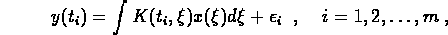
where the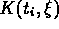 
are known, the 
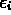are
measuring errors, and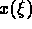 
is an unknown function to be determined.
Since these integral equations are ubiquitous in measurement processes, methods
for solving them are of great interest to NIST and ACMD.
Replacing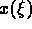 
by a discrete approximation 
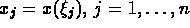, gives the linear regression model
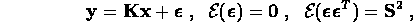
where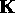 
is an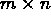 
matrix and 
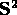is the covariance
matrix for the measurements. The corresponding least squares
problem is usually so poorly conditioned that the usual methods give wildly
oscillating, unphysical solutions.
This project previously produced
three algorithms, CLASIC, FERDIT and BRAKET-LS, which give
estimates and confidence intervals for the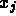 
.
CLASIC uses a singular value decomposition (SVD) of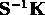 
to implement iterative refinement on the augmented system
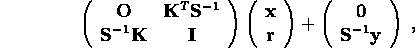
with an option for truncating the SVD to suppress the amplification of measurement noise.
The FERDIT algorithm assumes that the solution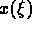 
is nonnegative and
iterates on a regularized regression model
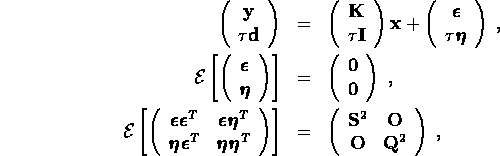
where 
is the regularization parameter,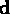 
is a positive vector
and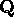 
is a related nonnegative diagonal matrix designed to constrain
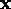to the positive orthant. The iteration is implemented with an SVD
of the matrix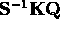 
. The bounds obtained are conservative and
suboptimal, but are useful as starting estimates for the BRAKET-LS method.
The BRAKET-LS algorithm also assumes a nonnegative solution and uses a parametric quadratic programming procedure to produce rigorous confidence interval bounds defined by
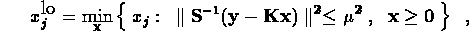
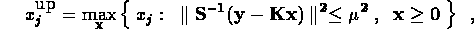
where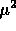 
is a constant chosen to give the desired confidence level.
The method requires initial estimates which do not have to bracket
the 
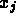very closely, but the computational effort is
considerably reduced by using the
suboptimal bounds obtained from the FERDIT method.
Current efforts have been devoted to simplifying and documenting the Fortran subroutines and writing a paper describing the BRAKET-LS software.