
Up: Numerical Evaluation of Special
Previous: A Note on the
- AB87a
-
G. Allasia and R. Besenghi, Numerical calculation of incomplete gamma
functions by the trapezoidal rule, Numer. Math. 50 (1987),
419-428.
- AB87b
-
G. Allasia and R. Besenghi, Numerical computation of Tricomi's psi
function by the trapezoidal rule, Computing 39 (1987), 271-279.
- AB89
-
G. Allasia and R. Besenghi, Numerical calculation of the Riemann zeta
function and generalizations by means of the trapezoidal rule, Numerical and
Applied Mathematics, Part 2 (Paris 1988) (C. Brezinski, ed.), IMACS Ann.
Comput. Appl. Math., 1.2, Baltzer, Basel, 1989, pp. 467-472.
- AB91
-
G. Allasia and R. Besenghi, Numerical evaluation of the Kummer function
with complex argument by the trapezoidal rule, Rend. Sem. Mat. Univ.
Politec. Torino 49 (1991), no. 3, 315-327 (1993).
- Ach86
-
J.-J. Achenbach, Numerik. Implementierung von Zylinderfunktionen,
Friedr. Vieweg & Sohn, Braunschweig/Wiesbaden, 1986.
- ACJP85
-
J. Arazy, T. Claesson, S. Janson, and J. Peetre, Means and their
iterations, Proceedings of the Nineteenth Nordic Congress of Mathematicians,
Reykjavik 1984, Icelandic Mathematical Society, Reykjavik, 1985,
pp. 191-212.
- ACM
-
Collected algorithms from ACM, Association for Computing Machinery,
1515 Broadway, New York, New York 10036, periodically updated looseleaf
collection.
- ACM64
-
Index by subject to algorithms, 1960-63, Comm. ACM 7 (1964),
146-148.
- AD79
-
D. E. Amos and S. L. Daniel, AMOSLIB, a special function library,
version 9/77, Report 77-1390, Sandia Laboratories, August 1979.
- Ada69
-
A. G. Adams, Algorithm 39. Areas under the normal curve, Comput. J.
12 (1969), 197-198.
- ADK+84
-
A. A. Abramov, A. L. Dyshko, N. B. Konyukhova, T. V. Pak, and B. S. Pariiskii,
Evaluation of prolate spheroidal function by solving the corresponding
differential equations, U.S.S.R. Comput. Math. and Math. Phys. 24
(1984), no. 1, 1-11.
- ADKL89
-
A. A. Abramov, A. L. Dyshko, N. B. Konyukhova, and T. V. Levitina,
Evaluation of Lamé angular wave functions by solving auxiliary
differential equations, U.S.S.R. Comput. Math. and Math. Phys. 29
(1989), no. 3, 119-131.
- ADKL91
-
A. A. Abramov, A. L. Dyshko, N. B. Konyukhova, and T. V. Levitina,
Computation of radial wave functions for spheroids and triaxial
ellipsoids by the modified phase function method, Comput. Math. Math. Phys.
31 (1991), no. 2, 25-42.
- ADW77a
-
D. E. Amos, S. L. Daniel, and M. K. Weston, Algorithm 511. CDC 6600
subroutines IBESS and JBESS for Bessel functions
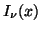 and
and
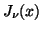 ,
,  ,
,  , ACM Trans. Math. Software 3
(1977), 93-95, for erratum see same journal v. 4 (1978), p. 411.
, ACM Trans. Math. Software 3
(1977), 93-95, for erratum see same journal v. 4 (1978), p. 411.
- ADW77b
-
D. E. Amos, S. L. Daniel, and M. K. Weston, CDC 6600 subroutines
IBESS and JBESS for Bessel functions
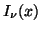 and
and
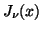 ,
,
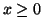 ,
, 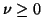 , ACM Trans. Math. Software 3 (1977), 76-92.
, ACM Trans. Math. Software 3 (1977), 76-92.
- Air84
-
T. J. Aird, The IMSL library, Sources and Development of Mathematical
Software (W. R. Cowell, ed.), Prentice-Hall, Inc., Englewood Cliffs, New
Jersey, 1984, pp. 264-301.
- Alh96
-
Fayez A. Alhargan, A complete method for the computations of Mathieu
characteristic numbers of integer orders, SIAM Rev. 38 (1996),
no. 2, 239-255.
- AM61
-
A. M. Arthurs and R. McCarroll, Expansion of spherical Bessel functions
in a series of Chebyshev polynomials, Math. Comp. 15 (1961),
159-162.
- AM78
-
R. W. B. Ardill and K. J. M. Moriarty, Spherical Bessel functions
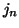 and
and 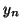 of integer order and real argument, Comput. Phys. Comm.
14 (1978), 261-265.
of integer order and real argument, Comput. Phys. Comm.
14 (1978), 261-265.
- Amo74
-
D. E. Amos, Computation of modified Bessel functions and their ratios,
Math. Comp. 28 (1974), 239-251.
- Amo80a
-
D. E. Amos, Algorithm 556. Exponential integrals, ACM Trans. Math.
Software 6 (1980), 420-428, for remark see same journal v. 9
(1983), p. 525.
- Amo80b
-
D. E. Amos, Computation of exponential integrals, ACM Trans. Math.
Software 6 (1980), 365-377.
- Amo83a
-
D. E. Amos, Algorithm 609. A portable Fortran subroutine for the
Bickley functions
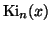 , ACM Trans. Math. Software
9 (1983), 480-493.
, ACM Trans. Math. Software
9 (1983), 480-493.
- Amo83b
-
D. E. Amos, Algorithm 610. A portable Fortran subroutine for
derivatives of the psi function, ACM Trans. Math. Software 9
(1983), 494-502.
- Amo83c
-
D. E. Amos, Uniform asymptotic expansions for exponential integrals
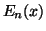 and Bickley functions
and Bickley functions
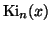 , ACM Trans.
Math. Software 9 (1983), 467-479.
, ACM Trans.
Math. Software 9 (1983), 467-479.
- Amo86
-
D. E. Amos, Algorithm 644. A portable package for Bessel functions of
a complex argument and nonnegative order, ACM Trans. Math. Software
12 (1986), 265-273, for remarks see same journal v. 16 (1990), p.
404 and v. 21 (1995), pp. 388-393.
- Amo90a
-
D. E. Amos, Algorithm 683. A portable Fortran subroutine for
exponential integrals of a complex argument, ACM Trans. Math. Software
16 (1990), 178-182.
- Amo90b
-
D. E. Amos, Computation of exponential integrals of a complex argument,
ACM Trans. Math. Software 16 (1990), 169-177.
- And82a
-
W. L. Anderson, Algorithm 588. Fast Hankel transforms using related
and lagged convolutions, ACM Trans. Math. Software 8 (1982),
369-370.
- And82b
-
W. L. Anderson, Fast Hankel transforms using related and lagged
convolutions, ACM Trans. Math. Software 8 (1982), 344-368.
- AS64
-
M. Abramowitz and I. A. Stegun (eds.), Handbook of mathematical functions
with formulas, graphs and mathematical tables, National Bureau of Standards
Applied Mathematics Series, vol. 55, U. S. Government Printing Office,
Washington, D. C., 1964.
- AS68
-
Statistical algorithms editorial note, Appl. Statist. 17
(1968), 79-82.
- AS92
-
J. Abad and J. Sesma, Computation of Coulomb wave functions at low
energies, Comput. Phys. Comm. 71 (1992), 110-124.
- AS93a
-
R. W. Abernathy and R. P. Smith, Algorithm 724. Program to calculate
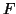 -percentiles, ACM Trans. Math. Software 19 (1993), 481-483.
-percentiles, ACM Trans. Math. Software 19 (1993), 481-483.
- AS93b
-
R. W. Abernathy and R. P. Smith, Applying series expansion to the inverse
beta distribution to find percentiles of the
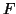 -distribution, ACM Trans.
Math. Software 19 (1993), 474-480.
-distribution, ACM Trans.
Math. Software 19 (1993), 474-480.
- Ask89
-
R. A. Askey, Handbooks of special functions, A Century of Mathematics in
America, Part III, Hist. Math., vol. 3, American Mathematical Society,
Providence, Rhode Island, 1989, pp. 369-391.
- ATZ83
-
F. M. Arscott, P. J. Taylor, and R. V. M. Zahar, On the numerical
construction of ellipsoidal wave functions, Math. Comp. 40 (1983),
367-380.
- Bai93
-
D. H. Bailey, Algorithm 719. Multiprecision translation and execution
of Fortran programs, ACM Trans. Math. Software 19 (1993),
288-319.
- Bak92
-
L. Baker, C mathematical function handbook, McGraw-Hill, Inc., New York,
1992, includes diskette.
- Bar61
-
R. Barakat, Evaluation of the incomplete gamma function of imaginary
argument by Chebyshev polynomials, Math. Comp. 15 (1961), 7-11.
- Bar74
-
R. H. Barlow, Convergent continued fraction approximants to generalised
polylogarithms, BIT 14 (1974), 112-116.
- Bar76
-
A. R. Barnett, RCWFF--A modification of the real Coulomb
wavefunction program RCWFN, Comput. Phys. Comm. 11 (1976),
141-142.
- Bar81a
-
A. R. Barnett, An algorithm for regular and irregular Coulomb and
Bessel functions of real order to machine accuracy, Comput. Phys. Comm.
21 (1981), 297-314.
- Bar81b
-
A. R. Barnett, KLEIN: Coulomb functions for real
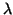 and
positive energy to high accuracy, Comput. Phys. Comm. 24 (1981),
141-159.
and
positive energy to high accuracy, Comput. Phys. Comm. 24 (1981),
141-159.
- Bar82a
-
A. R. Barnett, Continued-fraction evaluation of Coulomb functions
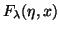 ,
,
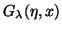 and their derivatives, J.
Comput. Phys. 46 (1982), 171-188.
and their derivatives, J.
Comput. Phys. 46 (1982), 171-188.
- Bar82b
-
A. R. Barnett, COULFG: Coulomb and Bessel functions and their
derivatives, for real arguments, by Steed's method, Comput. Phys. Comm.
27 (1982), 147-166.
- Bar82c
-
A. R. Barnett, High-precision evaluation of the regular and irregular
Coulomb wavefunctions, J. Comput. Appl. Math. 8 (1982), 29-33.
- BBC95
-
D. A. Barry, S. J. Barry, and P. J. Culligan-Hensley, Algorithm 743.
WAPR: A Fortran routine for calculating real values of the
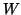 -function, ACM Trans. Math. Software 21 (1995), 172-181.
-function, ACM Trans. Math. Software 21 (1995), 172-181.
- BC83a
-
T. A. Beu and R. I. Câmpeanu, Prolate angular spheroidal wave
functions, Comput. Phys. Comm. 30 (1983), 187-192.
- BC83b
-
T. A. Beu and R. I. Câmpeanu, Prolate radial spheroidal wave
functions, Comput. Phys. Comm. 30 (1983), 177-185.
- BCB95
-
D. A. Barry, P. J. Culligan-Hensley, and S. J. Barry, Real values of
the
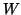 -function, ACM Trans. Math. Software 21 (1995), 161-171.
-function, ACM Trans. Math. Software 21 (1995), 161-171.
- BD80
-
A. Bañuelos and R. A. Depine, A program for computing the Riemann
zeta function for complex argument, Comput. Phys. Comm. 20 (1980),
441-445.
- BDG+72
-
C. Bardin, Y. Dandeu, L. Gauthier, J. Guillerman, T. Lena, and J.-M. Pernet,
Coulomb functions in the entire
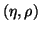 -plane, Comput. Phys.
Comm. 3 (1972), 73-87.
-plane, Comput. Phys.
Comm. 3 (1972), 73-87.
- BDM81
-
A. Bañuelos, R. A. Depine, and R. C. Mancini, A program for computing
the Fermi-Dirac functions, Comput. Phys. Comm. 21 (1981),
315-322.
- BEGG91
-
D. L. Boley, S. Elhay, G. H. Golub, and M. H. Gutknecht, Nonsymmetric
Lanczos and finding orthogonal polynomials associated with indefinite
weights, Numer. Algorithms 1 (1991), 21-43.
- BEJ76
-
J. M. Blair, C. A. Edwards, and J. H. Johnson, Rational Chebyshev
approximations for the inverse of the error function, Math. Comp.
30 (1976), 827-830.
- BEJ78
-
J. M. Blair, C. A. Edwards, and J. H. Johnson, Rational Chebyshev
approximations for the Bickley functions
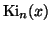 , Math.
Comp. 32 (1978), 876-886.
, Math.
Comp. 32 (1978), 876-886.
- Bel88
-
V. N. Belykh, Calculation on a computer of the complete elliptic
integrals
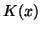 and
and 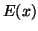 , Boundary value problems for partial
differential equations, Akad. Nauk SSSR Sibirsk. Otdel., Inst. Mat.,
Novosibirsk, 1988, pp. 3-15, 137 (Russian).
, Boundary value problems for partial
differential equations, Akad. Nauk SSSR Sibirsk. Otdel., Inst. Mat.,
Novosibirsk, 1988, pp. 3-15, 137 (Russian).
- BFST86
-
V. Bezvoda, R. Farzan, K. Segeth, and G. Takó, On numerical
evaluation of integrals involving Bessel functions, Apl. Mat. 31
(1986), 396-410.
- BG81a
-
G. A. Baker, Jr. and P. Graves-Morris, Padé approximants, part
I, Encyclopedia of Mathematics and its Applications, vol. 13,
Addison-Wesley Publishing Company, Reading, Massachusetts, 1981.
- BG81b
-
G. A. Baker, Jr. and P. Graves-Morris, Padé approximants, part
II, Encyclopedia of Mathematics and its Applications, vol. 14,
Addison-Wesley Publishing Company, Reading, Massachusetts, 1981.
- BGV93
-
K. Balla, O. S. Guk, and M. Vicsek, On the computation of Bessel
functions of first kind, Computing 50 (1993), 77-85.
- BH75
-
N. Bleistein and R. A. Handelsman, Asymptotic expansions of integrals,
Holt, Rinehart and Winston, New York, 1975.
- BHK91
-
R. F. Boisvert, S. E. Howe, and D. K. Kahaner, The guide to available
mathematical software problem classification system, Comm. Statist.
B--Simulation Comput. 20 (1991), 811-842.
- BHKS90
-
R. F. Boisvert, S. E. Howe, D. K. Kahaner, and J. L. Springmann, Guide to
available mathematical software, Tech. Report NISTIR 90-4237, National
Institute of Standards and Technology, Center for Computing and Applied
Mathematics, Gaithersburg, Maryland 20899, 1990.
- Bim93
-
HiQ reference manual, version 2.0, Bimillennium Corporation, 16795
Lark Avenue, Suite 200, Los Gatos, California 95030, 1993.
- Bis91
-
A. K. Bisoi, A Maple program to generate orthonormal polynomials,
Comput. Math. Appl. 22 (1991), no. 9, 1-5.
- BKN88a
-
L. V. Babushkina, M. K. Kerimov, and A. I. Nikitin, Algorithms for
computing Bessel functions of half-integer order with complex arguments,
U.S.S.R. Comput. Math. and Math. Phys. 28 (1988), no. 5, 109-117.
- BKN88b
-
L. V. Babushkina, M. K. Kerimov, and A. I. Nikitin, Algorithms for
evaluating spherical Bessel functions in the complex domain, U.S.S.R.
Comput. Math. and Math. Phys. 28 (1988), no. 6, 122-128.
- BL96
-
K. Balla and V. H. Linh, The simultaneous computation of Bessel
functions of first and second kind, Comput. Math. Appl. 31 (1996),
no. 4-5, 87-97, Selected topics in numerical methods (Miskolc, 1994).
- Bla46
-
G. Blanch, On the computation of Mathieu functions, J. Math. and Phys.
25 (1946), 1-20.
- Bla74
-
J. M. Blair, Rational Chebyshev approximations for the modified
Bessel functions
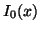 and
and 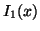 , Math. Comp. 28
(1974), 581-583.
, Math. Comp. 28
(1974), 581-583.
- BMOF92
-
E. Badralexe, P. Marksteiner, Y. Oh, and A. J. Freeman, Computation of
the Kummer functions and Whittaker functions by using Neumann type
series expansions, Comput. Phys. Comm. 71 (1992), 47-55.
- BN89
-
J. L. Blanchard and E. H. Newman, Numerical evaluation of parabolic
cylinder functions, IEEE Trans. Antennas and Propagation 37 (1989),
519-523.
- Boe60
-
J. Boersma, Computation of Fresnel integrals, Math. Comp. 14
(1960), 380.
- Bow84
-
K. O. Bowman, Computation of the polygamma functions, Comm. Statist.
B--Simulation Comput. 13 (1984), 409-415.
- BP96
-
R. Barakat and E. Parshall, Numerical evaluation of the zero-order
Hankel transform using Filon quadrature philosophy, Appl. Math. Lett.
9 (1996), no. 5, 21-26.
- BR71
-
R. D. Bardo and K. Ruedenberg, Numerical analysis and evaluation of
normalized repeated integrals of the error function and related functions,
J. Comput. Phys. 8 (1971), 167-174.
- BR91
-
C. Brezinski and M. Redivo Zaglia, A new presentation of orthogonal
polynomials with applications to their computation, Numer. Algorithms
1 (1991), 207-221.
- Bra73
-
W. J. Braithwaite, Associated Legendre polynomials, ordinary and
modified spherical harmonics, Comput. Phys. Comm. 5 (1973),
390-394.
- Bre76
-
R. P. Brent, Fast multiple-precision evaluation of elementary functions,
J. Assoc. Comput. Mach. 23 (1976), 242-251.
- Bre78a
-
R. P. Brent, Algorithm 524. MP, a Fortran multiple-precision
arithmetic package, ACM Trans. Math. Software 4 (1978), 71-81, for
remark see same journal v. 5 (1979), pp. 518-519.
- Bre78b
-
R. P. Brent, A Fortran multiple-precision arithmetic package, ACM
Trans. Math. Software 4 (1978), 57-70.
- Bre91
-
C. Brezinski, History of continued fractions and Padé
approximants, Springer Series in Computational Mathematics, vol. 12,
Springer-Verlag, Berlin, 1991.
- Bri95
-
E. Brizuela, Accurate normalisation of the beta-function PDF, J.
Computational Phys. 119 (1995), 385-387.
- BS80
-
K. L. Bell and N. S. Scott, Coulomb functions (negative
energies), Comput. Phys. Comm. 20 (1980), 447-458.
- BS92
-
R. F. Boisvert and B. V. Saunders, Portable vectorized software for
Bessel function evaluation, ACM Trans. Math. Software 18 (1992),
456-469, for corrigendum see same journal v. 19 (1993), p. 131.
- Bui91
-
Bui Doan Khanh, A computation of the Fermi-Dirac integrals by
asymptotics and the Hermite corrector formula, Appl. Math. Comput.
41 (1991), 61-68.
- Bul65a
-
R. Bulirsch, Numerical calculation of elliptic integrals and elliptic
functions, Numer. Math. 7 (1965), 78-90.
- Bul65b
-
R. Bulirsch, Numerical calculation of elliptic integrals and elliptic
functions. II, Numer. Math. 7 (1965), 353-354.
- Bul67
-
R. Bulirsch, Numerical calculation of the sine, cosine and Fresnel
integrals, Numer. Math. 9 (1967), 380-385.
- Bul69a
-
R. Bulirsch, An extension of the Bartky-transformation to incomplete
elliptic integrals of the third kind, Numer. Math. 13 (1969),
266-284.
- Bul69b
-
R. Bulirsch, Numerical calculation of elliptic integrals and elliptic
functions. III, Numer. Math. 13 (1969), 305-315.
- Bur63
-
F. D. Burgoyne, Approximations to Kelvin functions, Math. Comp.
17 (1963), 295-298.
- Buz84
-
B. L. Buzbee, The SLATEC common mathematical library, Sources and
Development of Mathematical Software (W. R. Cowell, ed.), Prentice-Hall,
Inc., Englewood Cliffs, New Jersey, 1984, pp. 302-320.
- BvI93
-
C. Brezinski and J. van Iseghem, Padé approximations, Handbook of
Numerical Analysis (P. G. Ciarlet and J. L. Lions, eds.), vol. 3,
North-Holland, Amsterdam, 1993, in press.
- BZ92
-
J. M. Borwein and I. J. Zucker, Fast evaluation of the gamma function for
small rational fractions using complete elliptic integrals of the first
kind, IMA J. Numer. Anal. 12 (1992), no. 4, 519-526.
- BZ95
-
M. C. Bartholomew-Biggs and S. Zakovic, Using Markov's interval
arithmetic to evaluate Bessel-Riccati functions, Numer. Algorithms
10 (1995), no. 3-4, 261-287.
- Cal88
-
J. Caldwell, Computation of eigenvalues of spheroidal harmonics using
relaxation, J. Phys. A 21 (1988), 3685-3693.
- Cam79
-
J. B. Campbell, Bessel functions
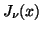 and
and
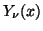 of
real order and real argument, Comput. Phys. Comm. 18 (1979),
133-142.
of
real order and real argument, Comput. Phys. Comm. 18 (1979),
133-142.
- Cam80
-
J. B. Campbell, On Temme's algorithm for the modified Bessel function
of the third kind, ACM Trans. Math. Software 6 (1980), 581-586.
- Cam81
-
J. B. Campbell, Bessel functions
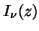 and
and
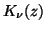 of real
order and complex argument, Comput. Phys. Comm. 24 (1981), 97-105,
for erratum see same journal v. 25 (1982), p. 207.
of real
order and complex argument, Comput. Phys. Comm. 24 (1981), 97-105,
for erratum see same journal v. 25 (1982), p. 207.
- Cam84
-
J. B. Campbell, Determination of
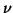 -zeros of Hankel functions,
Comput. Phys. Comm. 32 (1984), 333-339.
-zeros of Hankel functions,
Comput. Phys. Comm. 32 (1984), 333-339.
- Cam95
-
R. G. Campos, A quadrature formula for the Hankel transform, Numer.
Algorithms 9 (1995), no. 3-4, 343-354.
- Can71
-
J. Canosa, Numerical solution of Mathieu's equation, J. Comput. Phys.
7 (1971), 255-272.
- Can81
-
S. M. Candel, An algorithm for the Fourier-Bessel transform, Comput.
Phys. Comm. 23 (1981), 343-353.
- Car65
-
B. C. Carlson, On computing elliptic integrals and functions, J. Math.
and Phys. 44 (1965), 36-51.
- Car77a
-
B. C. Carlson, Elliptic integrals of the first kind, SIAM J. Math. Anal.
8 (1977), 231-242.
- Car77b
-
B. C. Carlson, Special functions of applied mathematics, Academic Press,
New York, 1977.
- Car79
-
B. C. Carlson, Computing elliptic integrals by duplication, Numer. Math.
33 (1979), 1-16.
- Car87
-
B. C. Carlson, A table of elliptic integrals of the second kind, Math.
Comp. 49 (1987), 595-606 and S13-S17.
- Car88
-
B. C. Carlson, A table of elliptic integrals of the third kind, Math.
Comp. 51 (1988), 267-280 and S1-S5.
- Car89
-
B. C. Carlson, A table of elliptic integrals: Cubic cases, Math. Comp.
53 (1989), 327-333.
- Car91
-
B. C. Carlson, A table of elliptic integrals: One quadratic factor,
Math. Comp. 56 (1991), 267-280.
- Car92
-
B. C. Carlson, A table of elliptic integrals: Two quadratic factors,
Math. Comp. 59 (1992), 165-180.
- Car95
-
B. C. Carlson, Numerical computation of real or complex elliptic
integrals, Numer. Algorithms 10 (1995), 13-26.
- CCF83
-
J. N. L. Connor, P. R. Curtis, and D. Farrelly, A differential equation
method for the numerical evaluation of the Airy, Pearcey and swallowtail
canonical integrals and their derivatives, Molecular Phys. 48
(1983), 1305-1330.
- CER93
-
CERNLIB short writeups, CERN Program Library Office, CERN-CN
Division, CH-1211 Geneva 23, Switzerland, 1993, electronic mail address is
cernlib@@cernvm.cern.ch.
- CF87
-
Ll. Closas and J. Fernández Rubio, Calculo rapido de las funciones
de Bessel modificadas
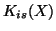 e
e
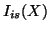 y sus derivadas,
Stochastica 11 (1987), no. 1, 53-61.
y sus derivadas,
Stochastica 11 (1987), no. 1, 53-61.
- CG89
-
G. Chiocchia and B. Gabutti, A new transformation for computing
hypergeometric series and the exact evaluation of the transonic adiabatic
flow over a smooth bump, Comput. & Fluids 17 (1989), no. 1,
13-23.
- CGL90
-
R. Coquereaux, A. Grossmann, and B. E. Lautrup, Iterative method for
calculation of the Weierstrass elliptic function, IMA J. Numer. Anal.
10 (1990), 119-128.
- CH67
-
W. J. Cody and K. E. Hillstrom, Chebyshev approximations for the natural
logarithm of the gamma function, Math. Comp. 21 (1967), 198-203.
- CH70a
-
J. A. Cochran and J. N. Hoffspiegel, Numerical techniques for finding
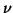 -zeros of Hankel functions, Math. Comp. 24 (1970),
413-422.
-zeros of Hankel functions, Math. Comp. 24 (1970),
413-422.
- CH70b
-
W. J. Cody and K. E. Hillstrom, Chebyshev approximations for the
Coulomb phase shift, Math. Comp. 24 (1970), 671-677, for
corrigendum, see same journal v. 26 (1972), p. 1031.
- Cha80
-
B. W. Char, On Stieltjes' continued fraction for the gamma function,
Math. Comp. 34 (1980), 547-551.
- Cha83
-
A. D. Chave, Numerical integration of related Hankel transforms by
quadrature and continued fraction expansion, Geophysics 48 (1983),
1671-1686.
- Chi92
-
R. C. Y. Chin, A domain decomposition method for generating orthogonal
polynomials for a Gaussian weight on a finite interval, J. Comput. Phys.
99 (1992), 321-336.
- Chr90
-
N. B. Christensen, Optimized fast Hankel transform filters, Geophys.
Prospecting 38 (1990), 545-568, for comment and reply, see same
journal v. 39 (1991), pp. 445-447 and 449-450.
- CHT71
-
W. J. Cody, K. E. Hillstrom, and H. C. Thacher, Jr., Chebyshev
approximations for the Riemann zeta function, Math. Comp. 25
(1971), 537-547.
- CJR92
-
R. M. Corless, D. J. Jeffrey, and H. Rasmussen, Numerical evaluation of
Airy functions with complex arguments, J. Comput. Phys. 99
(1992), 106-114.
- Cle62
-
C. W. Clenshaw, Chebyshev series for mathematical functions, National
Physical Laboratory Mathematical Tables, vol. 5, Her Majesty's Stationery
Office, London, 1962.
- Cle69
-
D. S. Clemm, Algorithm 352. Characteristic values and associated
solutions of Mathieu's differential equation, Comm. ACM 12
(1969), 399-407, for remarks see same journal v. 13 (1970), p. 750 and v. 15
(1972), p. 1074.
- CLM87
-
C. Chiccoli, S. Lorenzutta, and G. Maino, A numerical method for
generalized exponential integrals, Comput. Math. Appl. 14 (1987),
261-268.
- CLM88
-
C. Chiccoli, S. Lorenzutta, and G. Maino, On the evaluation of
generalized exponential integrals
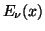 , J. Comput. Phys.
78 (1988), 278-287.
, J. Comput. Phys.
78 (1988), 278-287.
- CLM90a
-
C. Chiccoli, S. Lorenzutta, and G. Maino, An algorithm for exponential
integrals of real order, Computing 45 (1990), 269-276.
- CLM90b
-
C. Chiccoli, S. Lorenzutta, and G. Maino, Calculation of exponential
integrals of real order, Internat. J. Comput. Math. 31 (1990),
125-135.
- CLM90c
-
C. Chiccoli, S. Lorenzutta, and G. Maino, On a Tricomi series
representation for the generalized exponential integral, Internat. J.
Comput. Math. 31 (1990), 257-262.
- CLM97
-
C. Chiccoli, S. Lorenzutta, and G. Maino, On the evaluation of
generalized Laguerre functions, Atti Accad. Sci. Torino Cl. Sci. Fis. Mat.
Natur. 131 (1997), 77-90.
- CM78
-
J. N. L. Connor and D. C. Mackay, Accelerating the convergence of the
zonal harmonic series representation in the Schumann resonance problem, J.
Atmos. Terrestrial Physics 40 (1978), 977-980.
- CM79
-
J. N. L. Connor and D. C. Mackay, Calculation of angular distributions in
complex angular momentum theories of elastic scattering, Molecular Phys.
37 (1979), 1703-1712.
- CM83
-
J. P. Coleman and A. J. Monaghan, Chebyshev expansions for the Bessel
function
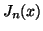 in the complex plane, Math. Comp. 40 (1983),
343-366.
in the complex plane, Math. Comp. 40 (1983),
343-366.
- CM84
-
A. P. Clarke and W. Marwood, A compact mathematical function package,
Austral. Comput. J. 16 (1984), 107-114.
- CMF77
-
W. J. Cody, R. M. Motley, and L. W. Fullerton, The computation of real
fractional order Bessel functions of the second kind, ACM Trans. Math.
Software 3 (1977), 232-239.
- CMW63
-
C. W. Clenshaw, G. F. Miller, and M. Woodger, Algorithms for special
functions I, Numer. Math. 4 (1963), 403-419.
- CN81
-
B. C. Carlson and E. M. Notis, Algorithm 577. Algorithms for incomplete
elliptic integrals, ACM Trans. Math. Software 7 (1981), 398-403.
- Cod65a
-
W. J. Cody, Chebyshev approximations for the complete elliptic integrals
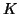 and
and 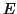 , Math. Comp. 19 (1965), 105-112, for corrigenda
see same journal v. 20 (1966), p. 207.
, Math. Comp. 19 (1965), 105-112, for corrigenda
see same journal v. 20 (1966), p. 207.
- Cod65b
-
W. J. Cody, Chebyshev polynomial expansions of complete elliptic
integrals, Math. Comp. 19 (1965), 249-259.
- Cod68
-
W. J. Cody, Chebyshev approximations for the Fresnel integrals, Math.
Comp. 22 (1968), 450-453, with Microfiche Supplement.
- Cod69
-
W. J. Cody, Rational Chebyshev approximations for the error function,
Math. Comp. 23 (1969), 631-637.
- Cod70
-
W. J. Cody, A survey of practical rational and polynomial approximation
of functions, SIAM Rev. 12 (1970), 400-423.
- Cod74
-
W. J. Cody, The construction of numerical subroutine libraries, SIAM
Rev. 16 (1974), 36-46.
- Cod75
-
W. J. Cody, The FUNPACK package of special function routines, ACM
Trans. Math. Software 1 (1975), 13-25.
- Cod76
-
W. J. Cody, An overview of software development for special functions,
Lecture Notes in Mathematics 506: Numerical Analysis Dundee, 1975 (G. A.
Watson, ed.), Springer-Verlag, Berlin, 1976, pp. 38-48.
- Cod80
-
W. J. Cody, Preliminary report on software for the modified Bessel
functions of the first kind, Tech. Memorandum TM-357, Argonne National
Laboratory, 9700 South Cass Avenue, Argonne, Illinois 60439-4801, 1980.
- Cod82
-
W. J. Cody, Implementation and testing of function software, Lecture
Notes in Computer Science No. 142. Problems and Methodologies in
Mathematical Software Production (P. C. Messina and A. Murli, eds.),
Springer-Verlag, Berlin, 1982, pp. 24-47.
- Cod83
-
W. J. Cody, Algorithm 597. Sequence of modified Bessel functions of
the first kind, ACM Trans. Math. Software 9 (1983), 242-245.
- Cod84a
-
W. J. Cody, FUNPACK--A package of special function routines,
Sources and Development of Mathematical Software (W. R. Cowell, ed.),
Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1984, pp. 49-67.
- Cod84b
-
W. J. Cody, Observations on the mathematical software effort, Sources
and Development of Mathematical Software (W. R. Cowell, ed.),
Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1984, pp. 1-19.
- Cod85
-
W. J. Cody, Software for special functions, Rend. Sem. Mat. Univ.
Politec. Torino Fascicolo Speciale. Special Functions: Theory and
Computation (1985), 91-116.
- Cod90a
-
W. J. Cody, The normal integral, Tech. Report MCS-89-1090, Mathematics
and Computer Science Division, Argonne National Laboratory, 9700 South Cass
Avenue, Argonne, Illinois 60439-4801, 1990.
- Cod90b
-
W. J. Cody, Performance evaluation of programs for the error and
complementary error functions, ACM Trans. Math. Software 16 (1990),
29-37.
- Cod91
-
W. J. Cody, Performance evaluation of programs related to the real gamma
function, ACM Trans. Math. Software 17 (1991), 46-54.
- Cod93a
-
W. J. Cody, Algorithm 714. CELEFUNT: A portable test package for
complex elementary functions, ACM Trans. Math. Software 19 (1993),
1-21.
- Cod93b
-
W. J. Cody, Algorithm 715. SPECFUN: A portable Fortran package of
special function routines and test drivers, ACM Trans. Math. Software
19 (1993), 22-32, for remark see same journal v. 22 (1996), p. 258.
- Cof91
-
M. W. Coffey, Calculation of generalized Lommel integrals for modified
Bessel functions, J. Phys. A 24 (1991), 23-33.
- Col80
-
J. P. Coleman, A Fortran subroutine for the Bessel function
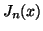 of order 0 to 10, Comput. Phys. Comm. 21 (1980),
109-118.
of order 0 to 10, Comput. Phys. Comm. 21 (1980),
109-118.
- Col87a
-
J. P. Coleman, Complex polynomial approximation by the Lanczos
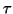 -method: Dawson's integral, J. Comput. Appl. Math. 20
(1987), 137-151.
-method: Dawson's integral, J. Comput. Appl. Math. 20
(1987), 137-151.
- Col87b
-
J. P. Coleman, Polynomial approximations in the complex plane, J.
Comput. Appl. Math. 18 (1987), 193-211.
- Coo68
-
B. E. Cooper, Algorithm AS 10. The use of orthogonal polynomials,
Appl. Statist. 17 (1968), 283-287.
- Cor72
-
P. Cornille, Computation of Hankel transforms, SIAM Rev. 14
(1972), 278-285.
- COT89
-
C. W. Clenshaw, F. W. J. Olver, and P. R. Turner, Level-index arithmetic:
An introductory survey, Lecture Notes in Mathematics 1397: Numerical
Analysis and Parallel Processing (Lancaster 1987) (P. R. Turner, ed.),
Springer-Verlag, Berlin, 1989, pp. 95-168.
- CP66
-
C. W. Clenshaw and S. M. Picken, Chebyshev series for Bessel functions
of fractional order, National Physical Laboratory Mathematical Tables,
vol. 8, Her Majesty's Stationery Office, London, 1966.
 P98
P98
-
P.
 ársky and M. Polášek, Incomplete gamma
ársky and M. Polášek, Incomplete gamma
 functions for real negative and complex arguments, J. Computational
Phys. 143 (1998), 259-265.
functions for real negative and complex arguments, J. Computational
Phys. 143 (1998), 259-265.
- CPC84
-
Master index volumes 1-30, July 1969--December 1983, Comput. Phys.
Comm. 35 (1984), B1-B75, C1-C928.
- CPC87
-
Program master index volumes 1-40, July 1969--June 1986, Comput.
Phys. Comm. (1987), 1-75.
- CPC90
-
Master index volumes 41-50, July 1986--July 1988, Comput. Phys.
Comm. (1990), 17-30.
- CPT70
-
W. J. Cody, K. A. Paciorek, and H. C. Thacher, Jr., Chebyshev
approximations for Dawson's integral, Math. Comp. 24 (1970),
171-178.
- Cra94
-
Isabella Cravero, The computation of the zeros of Laguerre
polynomials, Atti Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur. 128
(1994), no. 3-4, 105-115 (1995).
- Cra98
-
R. E. Crandall, Fast evaluation of multiple zeta sums, Math. Comp.
67 (1998), 1163-1172.
- Cri89
-
C. L. Critchfield, Computation of elliptic functions, J. Math. Phys.
30 (1989), 295-297.
- CS89
-
W. J. Cody and L. Stoltz, Performance evaluation of programs for certain
Bessel functions, ACM Trans. Math. Software 15 (1989), 41-48.
- CS91
-
W. J. Cody and L. Stoltz, The use of Taylor series to test accuracy of
function programs, ACM Trans. Math. Software 17 (1991), 55-63.
- CS93
-
A. S. Clarke and B. Shizgal, On the generation of orthogonal polynomials
using asymptotic methods for recurrence coefficients, J. Computational Phys.
104 (1993), 140-149.
- CS97
-
R. Chattamvelli and R. Shanmugam, Algorithm AS 310. Computing the
non-central beta distribution function, Appl. Statist. 46 (1997),
146-156.
- CST73
-
W. J. Cody, A. J. Strecok, and H. C. Thacher, Jr., Chebyshev
approximations for the psi function, Math. Comp. 27 (1973),
123-127.
- CT67
-
W. J. Cody and H. C. Thacher, Jr., Rational Chebyshev approximations
for Fermi-Dirac integrals of orders
 ,
, 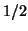 and
and 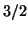 , Math. Comp.
21 (1967), 30-40.
, Math. Comp.
21 (1967), 30-40.
- CT68
-
W. J. Cody and H. C. Thacher, Jr., Rational Chebyshev approximations
for the exponential integral
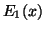 , Math. Comp. 22 (1968),
641-649.
, Math. Comp. 22 (1968),
641-649.
- CT69
-
W. J. Cody and H. C. Thacher, Jr., Chebyshev approximations for the
exponential integral
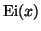 , Math. Comp. 23 (1969),
289-303.
, Math. Comp. 23 (1969),
289-303.
- CT85
-
M. Carmignani and A. Tortorici Macaluso, Calcolo delle funzioni
speciali
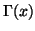 ,
,
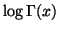 ,
,
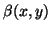 ,
,
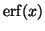 ,
,
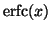 alle alte precisioni, Atti
Accad. Sci. Lett. Arti Palermo Ser. (5) 2 (1981-82) (1985), no. 1,
7-25.
alle alte precisioni, Atti
Accad. Sci. Lett. Arti Palermo Ser. (5) 2 (1981-82) (1985), no. 1,
7-25.
- CT94
-
J. A. Christley and I. J. Thompson, CRCWFN: coupled real Coulomb
wavefunctions, Comput. Phys. Comm. 79 (1994), 143-155.
- Cun69
-
S. W. Cunningham, Algorithm AS 24. From normal integral to deviate,
Appl. Statist. 18 (1969), 290-293.
- CW80
-
W. J. Cody and W. Waite, Software manual for the elementary functions,
Prentice Hall, Englewood Cliffs, New Jersey, 1980.
- Del73
-
Delft Numerical Analysis Group, On the computation of Mathieu
functions, J. Engrg. Math. 7 (1973), 39-61.
- Del79
-
G. Delic, Chebyshev expansion of the associated Legendre polynomial
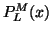 , Comput. Phys. Comm. 18 (1979), 63-71.
, Comput. Phys. Comm. 18 (1979), 63-71.
- dIVPM95
-
C. de Izarra, O. Vallée, J. Picart, and N. T. Minh, Computation of
the Whittaker functions
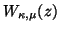 with series expansions and
Padé approximants, Comput. in Phys. 9 (1995), no. 3,
318-323.
with series expansions and
Padé approximants, Comput. in Phys. 9 (1995), no. 3,
318-323.
- DJ67
-
A. R. DiDonato and M. P. Jarnagin, The efficient calculation of the
incomplete beta-function ratio for half-integer values of the parameters
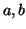 , Math. Comp. 21 (1967), 652-662.
, Math. Comp. 21 (1967), 652-662.
- DK90
-
S. L. Dvorak and E. F. Kuester, Numerical computation of the incomplete
Lipschitz-Hankel integral
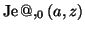 , J. Comput. Phys.
87 (1990), 301-327.
, J. Comput. Phys.
87 (1990), 301-327.
- DKK81
-
V. A. Ditkin, K. A. Karpov, and M. K. Kerimov, The computation of special
functions, U.S.S.R. Comput. Math. and Math. Phys. 20 (1981), no. 5,
3-12.
- DM86
-
A. R. DiDonato and A. H. Morris, Jr., Computation of the incomplete
gamma function ratios and their inverse, ACM Trans. Math. Software
12 (1986), 377-393.
- DM87
-
A. R. DiDonato and A. H. Morris, Jr., Algorithm 654. Fortran
subroutines for computing the incomplete gamma function ratios and their
inverse, ACM Trans. Math. Software 13 (1987), 318-319.
- DM92
-
A. R. DiDonato and A. H. Morris, Jr., Algorithm 708. Significant
digit computation of the incomplete beta function ratios, ACM Trans. Math.
Software 18 (1992), 360-373, for certification see same journal v.
20 (1994), pp. 393-397.
- DNM96
-
T. Do-Nhat and R. H. MacPhie, On the accurate computation of the prolate
spheroidal radial functions of the second kind, Quart. Appl. Math.
54 (1996), no. 4, 677-685.
- Dor68
-
E. Dorrer, Algorithm 322.
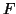 -distribution, Comm. ACM 11
(1968), 116-117, for certification see same journal v. 12 (1969), p. 39.
-distribution, Comm. ACM 11
(1968), 116-117, for certification see same journal v. 12 (1969), p. 39.
- DR94a
-
C. F. Dunkl and D. E. Ramirez, Algorithm 736. Hyperelliptic integrals
and the surface measure of ellipsoids, ACM Trans. Math. Software 20
(1994), 427-435.
- DR94b
-
C. F. Dunkl and D. E. Ramirez, Computing hyperelliptic integrals for
surface measure of ellipsoids, ACM Trans. Math. Software 20 (1994),
413-426.
- DR98
-
H.-J. Dobner and S. Ritter, Verified computation of Lamé functions
with high accuracy, Computing 60 (1998), 81-89.
- dT93
-
C. F. du Toit, Bessel functions
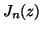 and
and
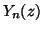 of
integer order and complex argument, Comput. Phys. Comm. 78 (1993),
no. 1-2, 181-189.
of
integer order and complex argument, Comput. Phys. Comm. 78 (1993),
no. 1-2, 181-189.
- DW95
-
K. Devlin and N. Wilson, Six-year index of ``Computers and
Mathematics'', Notices Amer. Math. Soc. 42 (1995), 248-254.
- Eck76
-
U. Eckhardt, A rational approximation to Weierstrass'
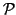 -function, Math. Comp. 30 (1976), 818-826.
-function, Math. Comp. 30 (1976), 818-826.
- Eck77
-
U. Eckhardt, A rational approximation to Weierstrass'
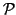 -function. II. The lemniscatic case, Computing 18
(1977), 341-349.
-function. II. The lemniscatic case, Computing 18
(1977), 341-349.
- Eck80
-
U. Eckhardt, Algorithm 549. Weierstrass' elliptic functions, ACM
Trans. Math. Software 4 (1980), 112-120.
- Egl84
-
A. P. Eglaya, Eigenvalues of wave spheroidal functions with a complex
parameter, Latv. Mat. Ezhegodnik (1984), no. 28, 143-150 (Russian).
- Ehr95
-
U. T. Ehrenmark, The numerical inversion of two classes of
Kontorovich-Lebedev transform by direct quadrature, J. Comput. Appl.
Math. 61 (1995), 43-72.
- EK92
-
Ö. E
 ecio
ecio lu and Ç. K. Koç, A parallel
algorithm for generating discrete orthogonal polynomials, Parallel Comput.
18 (1992), 649-659.
lu and Ç. K. Koç, A parallel
algorithm for generating discrete orthogonal polynomials, Parallel Comput.
18 (1992), 649-659.
- EKK85
-
A. Yu. Eremin, I. E. Kaporin, and M. K. Kerimov, The calculation of the
Riemann zeta-function in the complex domain, U.S.S.R. Comput. Math. and
Math. Phys. 25 (1985), no. 2, 111-119, see also [YKK88].
- EMOT53a
-
A. Erdélyi, W. Magnus, F. Oberhettinger, and F. G. Tricomi, Higher
transcendental functions, vol. 1, McGraw-Hill, New York, 1953, reprinted and
published in 1981 by Krieger Publishing Company, Melbourne, Florida.
- EMOT53b
-
A. Erdélyi, W. Magnus, F. Oberhettinger, and F. G. Tricomi, Higher
transcendental functions, vol. 2, McGraw-Hill, New York, 1953, reprinted and
published in 1981 by Krieger Publishing Company, Melbourne, Florida.
- EMOT55
-
A. Erdélyi, W. Magnus, F. Oberhettinger, and F. G. Tricomi, Higher
transcendental functions, vol. 3, McGraw-Hill, New York, 1955, reprinted and
published in 1981 by Krieger Publishing Company, Melbourne, Florida.
- EP69
-
S. P. Eraševskaja and A. A. Pal'cev, The computation of spheroidal
functions and their first derivatives on a computer. II, Vesc
 Akad.
Navuk BSSR Ser. F
Akad.
Navuk BSSR Ser. F z.-Mat. Navuk (1969), no. 4, 37-46 (Russian).
z.-Mat. Navuk (1969), no. 4, 37-46 (Russian).
- Eva74
-
D. J. Evans (ed.), Software for numerical mathematics, Proceedings of
the Loughboro University of Technology Conference of the IMA held in April
1973, Academic Press, London, 1974.
- EWB84
-
A. S. Elder, J. N. Walbert, and E. C. Benck, Calculation of Legendre
functions on the cut for integral order and complex degree by means of
Gauss continued fractions, Tech. Report ARBRL-MR-03335, U. S. Army
Armament Research and Development Center, Ballistic Research Laboratory,
Aberdeen Proving Ground, Maryland, 1984, copies obtainable from National
Technical Information Service, U. S. Dept. of Commerce, Springfield, VA
22161.
- Fet70
-
H. E. Fettis, A new method for computing toroidal harmonics, Math. Comp.
24 (1970), 667-670.
- Feu91
-
F. Feuillebois, Numerical calculation of singular integrals related to
Hankel transform, Comput. Math. Appl. 21 (1991), no. 2-3, 87-94.
- FG91
-
B. Fischer and G. H. Golub, On generating polynomials which are
orthogonal over several intervals, Math. Comp. 56 (1991), 711-730.
- FG92
-
B. Fischer and G. H. Golub, How to generate unknown orthogonal
polynomials out of known orthogonal polynomials, J. Comput. Appl. Math.
43 (1992), 99-115.
- FGG82
-
J. D. Fenton and R. S. Gardiner-Garden, Rapidly-convergent methods for
evaluating elliptic integrals and theta and elliptic functions, J. Austral.
Math. Soc. Ser. B 24 (1982), 47-58.
- FHS78a
-
P. A. Fox, A. D. Hall, and N. L. Schryer, Algorithm 528. Framework for
a portable library, ACM Trans. Math. Software 4 (1978), 177-188.
- FHS78b
-
P. A. Fox, A. D. Hall, and N. L. Schryer, The PORT mathematical
subroutine library, ACM Trans. Math. Software 4 (1978), 104-126.
- FI94
-
Toshio Fukushima and Hideharu Ishizaki, Numerical computation of
incomplete elliptic integrals of a general form, Celestial Mech. Dynam.
Astronom. 59 (1994), no. 3, 237-251.
- Fik68
-
C. T. Fike, Computer evaluation of mathematical functions,
Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1968.
- FL67
-
W. G. Fair and Y. L. Luke, Rational approximations to the incomplete
elliptic integrals of the first and second kinds, Math. Comp. 21
(1967), 418-422.
- Fle68
-
O. L. Fleckner, A method for the computation of the Fresnel integrals
and related functions, Math. Comp. 22 (1968), 635-640.
- FO94
-
H. Früchtl and P. Otto, A new algorithm for the evaluation of the
incomplete gamma function on vector computers, ACM Trans. Math. Software
20 (1994), 436-446.
- For97
-
R. C. Forrey, Computing the hypergeometric function, J. Computational
Phys. 137 (1997), 79-100.
- Fox56
-
L. Fox, The use and construction of mathematical tables, National
Physical Laboratory Mathematical Tables, vol. 1, Her Majesty's Stationery
Office, London, 1956.
- Fox84
-
P. A. Fox, The PORT mathematical subroutine library, Sources and
Development of Mathematical Software (W. R. Cowell, ed.), Prentice-Hall,
Inc., Englewood Cliffs, New Jersey, 1984, pp. 346-374.
- FP68
-
L. Fox and I. B. Parker, Chebyshev polynomials in numerical analysis,
Oxford University Press, London, 1968.
- FP84
-
B. Ford and J. C. T. Pool, The evolving NAG library service, Sources
and Development of Mathematical Software (W. R. Cowell, ed.), Prentice-Hall,
Inc., Englewood Cliffs, New Jersey, 1984, pp. 375-397.
- FR86
-
L. W. Fullerton and G. A. Rinker, Generalized Fermi-Dirac
integrals--FD, FDG, FDH, Comput. Phys. Comm. 39 (1986),
181-185.
- FS67
-
A. M. S. Filho and G. Schwachheim, Algorithm 309. Gamma function with
arbitrary precision, Comm. ACM 10 (1967), 511-512.
- Ful72
-
L. W. Fullerton, Algorithm 435. Modified incomplete gamma function,
Comm. ACM 15 (1972), 993-995, for remark see ACM Trans. Math.
Software v. 4 (1978), pp. 296-304.
- Ful77
-
L. W. Fullerton, Portable special function routines, Lecture Notes in
Computer Science 57: Portability of Numerical Software (Oak Brook 1976)
(W. R. Cowell, ed.), Springer-Verlag, Berlin, 1977, pp. 452-483.
- Ful80
-
L. W. Fullerton, A bibliography on the evaluation of mathematical
functions, Computing Science Tech. Report No. 86, Bell Laboratories, Murray
Hill, New Jersey 07974, 1980.
- FW80
-
A. Fransén and S. Wrigge, High-precision values of the gamma function
and of some related coefficients, Math. Comp. 34 (1980), 553-566,
for addendum and corrigendum see same journal v. 37 (1981), pp. 233-235.
- Gab79
-
B. Gabutti, On high precision methods for computing integrals involving
Bessel functions, Math. Comp. 33 (1979), 1049-1057.
- Gab80
-
B. Gabutti, On the generalization of a method for computing Bessel
function integrals, J. Comput. Appl. Math. 6 (1980), 167-168.
- Gaf88
-
P. W. Gaffney, When things go wrong
 , Pitman Research Notes in
Mathematics Series (D. F. Griffiths and G. A. Watson, eds.), vol. 170,
Longman Scientific and Technical, Harlow, Essex, U. K., 1988, pp. 67-114.
, Pitman Research Notes in
Mathematics Series (D. F. Griffiths and G. A. Watson, eds.), vol. 170,
Longman Scientific and Technical, Harlow, Essex, U. K., 1988, pp. 67-114.
- Gau64
-
W. Gautschi, Algorithm 222. Incomplete beta function ratios, Comm. ACM
7 (1964), 143-144, for certification see same journal v. 7 (1964),
p. 244.
- Gau65
-
W. Gautschi, Algorithm 259. Legendre functions for arguments larger
than one, Comm. ACM 8 (1965), 488-492, for remark see ACM Trans.
Math. Software, v. 3 (1977), pp. 204-205.
- Gau69a
-
W. Gautschi, Algorithm 363. Complex error function, Comm. ACM
12 (1969), 635, for certification see same journal v. 15 (1972), pp.
465-466.
- Gau69b
-
W. Gautschi, An application of minimal solutions of three-term
recurrences to Coulomb wave functions, Aequationes Math. 2
(1969), 171-176.
- Gau70
-
W. Gautschi, Efficient computation of the complex error function, SIAM
J. Numer. Anal. 7 (1970), 187-198.
- Gau73
-
W. Gautschi, Algorithm 471. Exponential integrals, Comm. ACM
16 (1973), 761-763.
- Gau75
-
W. Gautschi, Computational methods in special functions--a survey,
Theory and application of special functions, Proc. Advanced Sem., Math. Res.
Center, Univ. Wisconsin, Madison, Wis., Academic Press, New York, 1975,
pp. 1-98.
- Gau77a
-
W. Gautschi, Algorithm 521. Repeated integrals of the coerror
function, ACM Trans. Math. Software 3 (1977), 301-302.
- Gau77b
-
W. Gautschi, Evaluation of the repeated integrals of the coerror
function, ACM Trans. Math. Software 3 (1977), 240-252.
- Gau79a
-
W. Gautschi, Algorithm 542. Incomplete gamma functions, ACM Trans.
Math. Software 5 (1979), 482-489.
- Gau79b
-
W. Gautschi, A computational procedure for incomplete gamma functions,
ACM Trans. Math. Software 5 (1979), 466-481.
- Gau82
-
W. Gautschi, On generating orthogonal polynomials, SIAM J. Sci. Statist.
Comput. 3 (1982), 289-317.
- Gau85
-
W. Gautschi, Orthogonal polynomials--constructive theory and
applications, J. Comput. Appl. Math. 12/13 (1985), 61-76.
- Gau90
-
W. Gautschi, Computational aspects of orthogonal polynomials, Orthogonal
Polynomials: Theory and Practice (P. Nevai, ed.), Kluwer Academic
Publishers, Dordrecht, 1990, NATO ASI Series, vol. C294,
pp. 181-216.
- Gau91a
-
W. Gautschi, Computational problems and applications of orthogonal
polynomials, Orthogonal Polynomials and their Applications (C. Brezinski,
L. Gori, and A. Ronveaux, eds.), J. C. Baltzer AG, Scientific Publishing
Company, Basel, 1991, pp. 61-71.
- Gau91b
-
W. Gautschi, On the paper ``A continued fraction approximation of the
modified Bessel function
 '' by P. R. Parthasarathy and N.
Balakrishnan, Appl. Math. Lett. 4 (1991), no. 5, 47-51.
'' by P. R. Parthasarathy and N.
Balakrishnan, Appl. Math. Lett. 4 (1991), no. 5, 47-51.
- Gau93a
-
W. Gautschi, Gauss-type quadrature rules for rational functions,
International Series of Numerical Mathematics, vol. 112, Birkhäuser
Verlag, Basel, 1993, pp. 111-130.
- Gau93b
-
W. Gautschi, Is the recurrence relation for orthogonal polynomials always
stable?, BIT 33 (1993), 277-284.
- Gau93c
-
W. Gautschi, On the computation of generalized Fermi-Dirac and
Bose-Einstein integrals, Comput. Phys. Comm. 74 (1993),
233-238.
- Gau94
-
W. Gautschi, Algorithm 726. ORTHPOL--A package of routines for
generating orthogonal polynomials and Gauss-type quadrature rules, ACM
Trans. Math. Software 20 (1994), 21-62, for remark see same journal
v. 24 (1998), p. 355.
- Gau99
-
W. Gautschi, A note on the recursive calculation of incomplete gamma
functions, ACM Trans. Math. Software 25 (1999), 101-107.
- GB87
-
A. Ganguli and R. Baskaran, Generation of Bessel functions with complex
arguments and integer orders, Internat. J. Comput. Math. 21 (1987),
43-64.
- GH85
-
P. Griffiths and I. D. Hill (eds.), Applied statistics algorithms, Ellis
Horwood Limited, Chichester, 1985.
- GM81
-
B. Gabutti and B. Minetti, A new application of the discrete Laguerre
polynomials in the numerical evaluation of the Hankel transform of a
strongly decreasing even function, J. Comput. Phys. 42 (1981),
277-287.
- Goa95
-
M. Goano, Algorithm 745. Computation of the complete and incomplete
Fermi-Dirac integral, ACM Trans. Math. Software 21 (1995),
221-232, for remark see same journal v. 23 (1997), p. 295.
- Gor69
-
R. G. Gordon, New method for constructing wavefunctions for bound states
and scattering, J. Chem. Phys. 51 (1969), no. 1, 14-25.
- GP64
-
I. Gargantini and T. Pomentale, Rational Chebyshev approximations to
the Bessel function integrals
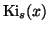 , Comm. ACM
7 (1964), 727-730.
, Comm. ACM
7 (1964), 727-730.
- GS78
-
W. Gautschi and J. Slavik, On the computation of modified Bessel
function ratios, Math. Comp. 32 (1978), 865-875.
- GS97
-
A. Gil and J. Segura, Evaluation of Legendre functions of argument
greater than one, Comput. Phys. Comm. 105 (1997), no. 2-3,
273-283.
- GS98
-
A. Gil and J. Segura, A code to evaluate prolate and oblate spheroidal
harmonics, Comput. Phys. Comm. 108 (1998), 267-278.
- GT81
-
R. Gastmans and W. Troost, On the evaluation of polylogarithmic
integrals, Simon Stevin 55 (1981), 205-219.
- Gue94
-
S. Gueron, Methods for fast computation of integral transforms, J.
Computational Phys. 110 (1994), 164-170.
- GZ75
-
E. S. Ginsberg and D. Zaborowski, Algorithm 490. The dilogarithm
function of a real argument, Comm. ACM 18 (1975), 200-202, for
remark see ACM Trans. Math. Software v. 2 (1976), p. 112.
- GZ95
-
W. Gautschi and M. Zhang, Computing orthogonal polynomials in Sobolev
spaces, Numer. Math. 71 (1995), 159-183.
- Ham85
-
D. E. Hamilton, Remark on Algorithm 620: References and keywords for
collected algorithms from ACM, ACM Trans. Math. Software 11
(1985), 305-307.
- Han85
-
E. W. Hansen, Fast Hankel transform algorithm, IEEE Trans. Acoust.
Speech Signal Process. 33 (1985), 666-671.
- HCL+68
-
J. F. Hart, E. W. Cheney, C. L. Lawson, H. J. Maehly, C. K. Mesztenyi, J. R.
Rice, H. C. Thacher, Jr., and C. Witzgall, Computer approximations,
John Wiley and Sons, Inc., New York, 1968.
- HD73
-
G. W. Hill and A. W. Davis, Algorithm 442. Normal deviate, Comm. ACM
16 (1973), 51-52.
- Hea85
-
M. A. Heald, Rational approximations for the Fresnel integrals, Math.
Comp. 44 (1985), 459-461.
- Hem81
-
P. W. Hemker (ed.), NUMAL numerical procedures in Algol 60,
Mathematisch Centrum Syllabus 47.1-7, Centrum voor Wiskunde en Informatica,
Kruislaan 413, 1098 SJ, Amsterdam, 1981.
- Hen79
-
P. Henrici, Zur numerischen Berechnung der Fresnelschen Integrale,
Z. Angew. Math. Phys. 30 (1979), 209-219.
- Hil70a
-
G. W. Hill, Algorithm 395. Student's
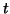 -distribution, Comm. ACM
13 (1970), 617-619, for remarks see ACM Trans. Math. Software v. 5
(1979), pp. 238-239, v. 7 (1981), pp. 247-249.
-distribution, Comm. ACM
13 (1970), 617-619, for remarks see ACM Trans. Math. Software v. 5
(1979), pp. 238-239, v. 7 (1981), pp. 247-249.
- Hil70b
-
G. W. Hill, Algorithm 396. Student's
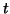 -quantiles, Comm. ACM
13 (1970), 619-620, for remarks see ACM Trans. Math. Software v. 5
(1979), pp. 238-239, v. 7 (1981), pp. 250-251.
-quantiles, Comm. ACM
13 (1970), 619-620, for remarks see ACM Trans. Math. Software v. 5
(1979), pp. 238-239, v. 7 (1981), pp. 250-251.
- Hil73
-
I. D. Hill, Algorithm AS 66. The normal integral, Appl. Statist.
22 (1973), 424-427.
- Hil77
-
G. W. Hill, Algorithm 518. Incomplete Bessel function
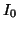 :
The von Mises distribution, ACM Trans. Math. Software 3 (1977),
279-284.
:
The von Mises distribution, ACM Trans. Math. Software 3 (1977),
279-284.
- Hil81
-
G. W. Hill, Algorithm 571. Statistics for von Mises' and Fisher's
distributions of directions:
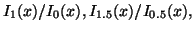 and their inverses, ACM Trans. Math. Software 7 (1981), 233-238.
and their inverses, ACM Trans. Math. Software 7 (1981), 233-238.
- Hit68
-
S. Hitotumatu, On the numerical computation of Bessel functions through
continued fraction, Comment. Math. Univ. St. Paul. 16 (1967/68),
89-113.
- HM90a
-
T. R. Hopkins and D. R. Morse, Index of statistical algorithms, Appl.
Statist. 39 (1990), 177-187.
- HM90b
-
T. R. Hopkins and D. R. Morse, Remark on Algorithm 620: References
and keywords for collected algorithms from ACM, ACM Trans. Math. Software
16 (1990), 401-403.
- HN97a
-
M. Hiyama and H. Nakamura, Gaussian expansions of the two-center
Coulomb functions, Comput. Phys. Comm. 103 (1997), 197-208.
- HN97b
-
M. Hiyama and H. Nakamura, Two-center Coulomb functions, Comput.
Phys. Comm. 103 (1997), 209-216.
- Hod70
-
D. B. Hodge, Eigenvalues and eigenfunctions of the spheroidal wave
equation, J. Math. Phys. 11 (1970), 2308-2312.
- HR72
-
D. B. Hunter and T. Regan, A note on the evaluation of the complementary
error function, Math. Comp. 26 (1972), 539-541.
- Hsu93
-
Yupai P. Hsu, Development of a Gaussian hypergeometric function code in
complex domains, Internat. J. Modern Phys. C 4 (1993), no. 4,
805-840.
- Hum64
-
D. G. Hummer, Expansion of Dawson's function in a series of Chebyshev
polynomials, Math. Comp. 18 (1964), 317-319.
- Hun95
-
D. B. Hunter, The evaluation of Legendre functions of the second kind,
Numer. Algorithms 10 (1995), 41-49.
- IKF91
-
Y. Ikebe, Y. Kikuchi, and I. Fujishiro, Computing zeros and orders of
Bessel functions, J. Comput. Appl. Math. 38 (1991), 169-184.
- IKF+93
-
Yasuhiko Ikebe, Yasushi Kikuchi, Issei Fujishiro, Nobuyoshi Asai, Kouichi
Takanashi, and Minoru Harada, The eigenvalue problem for infinite
compact complex symmetric matrices with application to the numerical
computation of complex zeros of
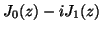 and of Bessel
functions
and of Bessel
functions
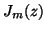 of any real order
of any real order 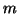 , Linear Algebra Appl.
194 (1993), 35-70.
, Linear Algebra Appl.
194 (1993), 35-70.
- IKJ95
-
M. Ikonomou, P. Köhler, and A. F. Jacob, Computation of integrals
over the half-line involving products of Bessel functions, with application
to microwave transmission lines, Z. Angew. Math. Mech. 75 (1995),
no. 12, 917-926.
- IMS91
-
MATH/LIBRARY special functions, version 2.0, Visual Numerics, Inc.,
2500 Wilcrest Drive, Suite 200, Houston, Texas 77042, 1991, see also
http://www.vni.com/.
- Jab94
-
A. Jablonski, Numerical evaluation of spherical Bessel functions of the
first kind, J. Computational Phys. 111 (1994), 256-259.
- JE45
-
E. Jahnke and F. Emde, Tables of functions with formulae and curves,
fourth ed., Dover Publications, Inc., New York, 1945.
- JEL60
-
E. Jahnke, F. Emde, and F. Lösch, Tables of higher functions, sixth
ed., McGraw-Hill, New York, 1960.
- JL72
-
D. Jacobs and F. Lambert, On the numerical calculation of
polylogarithms, BIT 12 (1972), 581-585.
- Joh75
-
H. K. Johansen, An interactive computer/graphic-display-terminal system
for interpretation of resistivity soundings, Geophys. Prospecting
23 (1975), 449-458.
- JT80
-
W. B. Jones and W. J. Thron, Continued fractions: Analytic theory and
applications, Encyclopedia of Mathematics and its Applications, vol. 11,
Addison-Wesley Publishing Company, Reading, Massachusetts, 1980.
- JT85
-
W. B. Jones and W. J. Thron, On the computation of incomplete gamma
functions in the complex domain, J. Comput. Appl. Math. 12/13
(1985), 401-417.
- Kae95
-
T. A. Kaeding, Pascal program for generating tables of SU(3)
Clebsch-Gordan coefficients, Comput. Phys. Comm. 85 (1995),
82-88.
- Kal92
-
S. L. Kalla, On the evaluation of the Gauss hypergeometric function,
C. R. Acad. Bulgare Sci. 45 (1992), no. 6, 35-36.
- Kar91
-
E. A. Karatsuba, Fast evaluation of transcendental functions, Problems
Inform. Transmission 27 (1991), 339-360.
- Kat78
-
C. R. Katholi, On the computation of values of the psi function from
rapidly converging power series expansions, J. Statist. Comput. Simulation
8 (1978), 25-42.
- KBH70
-
B. J. King, R. V. Baier, and S. Hanish, A Fortran computer program for
calculating the prolate spheroidal radial functions of the first and second
kind and their first derivatives, NRL Report No. 7012, Naval Res. Lab.,
Washington, D. C., 1970.
- Ker80
-
M. K. Kerimov, Methods of computing the Riemann zeta-function and some
generalizations of it, U.S.S.R. Comput. Math. and Math. Phys. 20
(1980), no. 6, 212-230.
- KG80
-
W. J. Kennedy, Jr. and J. E. Gentle, Statistical computing, Marcel
Dekker, New York, 1980.
- Kha97
-
H. G. Khajah, Tau method approximation of the Gauss hypergeometric
function, C. R. Acad. Bulgare Sci. 50 (1997), no. 6, 13-16.
- Kin88
-
A. C. King, Periodic approximations to an elliptical function, Appl.
Anal. 27 (1988), no. 4, 271-278.
- KMR70
-
K. S. Kölbig, J. A. Mignaco, and E. Remiddi, On Nielsen's
generalized polylogarithms and their numerical calculation, BIT 10
(1970), 38-73.
- Köl72a
-
K. S. Kölbig, Programs for computing the logarithm of the gamma
function, and the digamma function, for complex argument, Comput. Phys.
Comm. 4 (1972), 221-226.
- Köl72b
-
K. S. Kölbig, Remarks on the computation of Coulomb wavefunctions,
Comput. Phys. Comm. 4 (1972), 214-220.
- Köl81
-
K. S. Kölbig, A program for computing the conical functions of the
first kind
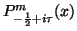 for
for 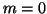 and
and 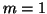 , Comput.
Phys. Comm. 23 (1981), 51-61.
, Comput.
Phys. Comm. 23 (1981), 51-61.
- Köl95
-
K. S. Kölbig, Chebyshev coefficients for the Clausen function
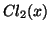 , J. Comput. Appl. Math. 64 (1995), 295-297.
, J. Comput. Appl. Math. 64 (1995), 295-297.
- Kon96
-
E. Konishi, Calculation of complex polygamma functions, Sci. Rep.
Hirosaki Univ. 43 (1996), 161-183.
- Krä90
-
W. Krämer, Berechnung der Gammafunktion
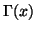 für
reelle Punkt- und Intervallargumente, Z. Angew. Math. Mech.
70 (1990), T581-T584.
für
reelle Punkt- und Intervallargumente, Z. Angew. Math. Mech.
70 (1990), T581-T584.
- Kro91
-
F. T. Krogh, ACM algorithms policy, ACM Trans. Math. Software
17 (1991), 427-430.
- KRVZ98
-
P. Kravanja, O. Ragos, M. N. Vrahatis, and F. A. Zafiropoulos, ZEBEC:
A mathematical software package for computing simple zeros of Bessel
functions of real order and complex argument, Comput. Phys. Comm.
113 (1998), 220-238.
- KS84a
-
M. K. Kerimov and S. L. Skorokhodov, Calculation of modified Bessel
functions in the complex domain, U.S.S.R. Comput. Math. and Math. Phys.
24 (1984), no. 3, 15-24.
- KS84b
-
M. K. Kerimov and S. L. Skorokhodov, Calculation of the complex zeros of
the modified Bessel function of the second kind and its derivatives,
U.S.S.R. Comput. Math. and Math. Phys. 24 (1984), no. 4, 115-123.
- KS84c
-
M. K. Kerimov and S. L. Skorokhodov, Evaluation of complex zeros of
Bessel functions
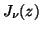 and
and
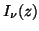 and their derivatives,
U.S.S.R. Comput. Math. and Math. Phys. 24 (1984), no. 5, 131-141.
and their derivatives,
U.S.S.R. Comput. Math. and Math. Phys. 24 (1984), no. 5, 131-141.
- KS84d
-
K. S. Kölbig and B. Schorr, A program package for the Landau
distribution, Comput. Phys. Comm. 31 (1984), 97-111.
- KS85a
-
M. K. Kerimov and S. L. Skorokhodov, Calculation of the complex zeros of
a Bessel function of the second kind and its derivatives, U.S.S.R. Comput.
Math. and Math. Phys. 25 (1985), no. 5, 117-128.
- KS85b
-
M. K. Kerimov and S. L. Skorokhodov, Calculation of the complex zeros of
Hankel functions and their derivatives, U.S.S.R. Comput. Math. and Math.
Phys. 25 (1985), no. 6, 26-36.
- KS85c
-
M. K. Kerimov and S. L. Skorokhodov, Calculation of the multiple zeros of
the derivatives of the cylindrical Bessel functions
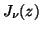 and
and
 , U.S.S.R. Comput. Math. and Math. Phys. 25 (1985),
no. 6, 101-107.
, U.S.S.R. Comput. Math. and Math. Phys. 25 (1985),
no. 6, 101-107.
- KS87
-
M. K. Kerimov and S. L. Skorokhodov, On the calculation of the multiple
complex roots of the derivatives of cylindrical Bessel functions, U.S.S.R.
Comput. Math. and Math. Phys. 27 (1987), no. 6, 18-25.
- Kuk71
-
H. Kuki, Mathematical function subprograms for basic system libraries--
objectives, constraints and trade-off, Mathematical Software (J. R. Rice,
ed.), Academic Press, New York, 1971, pp. 187-199.
- Kuk72a
-
H. Kuki, Algorithm 421. Complex gamma function with error control,
Comm. ACM 15 (1972), 271-272.
- Kuk72b
-
H. Kuki, Complex gamma function with error control, Comm. ACM
15 (1972), 262-267.
- KvB70
-
B. J. King and A. L. van Buren, A Fortran computer program for
calculating the prolate and oblate angle functions of the first kind and
their first and second derivatives, NRL Report No. 7161, Naval Res.
Lab., Washington, D. C., 1970.
- LCY65
-
L. A. Lyusternik, O. A. Chervonenkis, and A. R. Yanpol'skii, Handbook for
computing elementary functions, International Series of Monographs in Pure
and Applied Mathematics, vol. 76, Pergamon Press, Oxford, 1965.
- LDP93
-
Y. Li, X. Dong, and S. Pan, Computation of auxiliary functions in STO
molecular integrals up to arbitrary accuracy. I. Evaluation of incomplete
gamma function
 by forward recursion, Internat. J. Quantum Chem.
45 (1993), 3-14.
by forward recursion, Internat. J. Quantum Chem.
45 (1993), 3-14.
- Lee79
-
W. R. Leeb, Algorithm 537. Characteristic values of Mathieu's
differential equation, ACM Trans. Math. Software 5 (1979),
112-117.
- Lee80
-
S.-Y. Lee, The inhomogeneous Airy functions
 and
and
 , J. Chem. Phys. 72 (1980), 332-336.
, J. Chem. Phys. 72 (1980), 332-336.
- Lee90
-
D. K. Lee, Application of theta functions for numerical evaluation of
complete elliptic integrals of the first and second kinds, Comput. Phys.
Comm. 60 (1990), 319-327.
- Lee92
-
D. K. Lee, Calculation of coefficients in a power-series expansion of the
nome
![$ q = \exp[-\pi{K}(k')/{K}(k)]$](img95.gif) , Comput. Phys. Comm. 70 (1992),
292-296.
, Comput. Phys. Comm. 70 (1992),
292-296.
- Lem97
-
D. Lemoine, Optimal cylindrical and spherical Bessel transforms
satisfying bound state boundary conditions, Comput. Phys. Comm. 99
(1997), 297-306.
- Let96
-
Frank G. Lether, Rational approximation formulas for computing the
positive zeros of
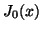 , J. Comput. Appl. Math. 67 (1996),
no. 1, 167-172.
, J. Comput. Appl. Math. 67 (1996),
no. 1, 167-172.
- Let97
-
Frank G. Lether, Constrained near-minimax rational approximations to
Dawson's integral, Appl. Math. Comput. 88 (1997), no. 2-3,
267-274.
- Let98
-
Frank G. Lether, Shifted rectangular quadrature rule approximations to
Dawson's integral
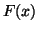 , J. Comput. Appl. Math. 92 (1998),
no. 2, 97-102.
, J. Comput. Appl. Math. 92 (1998),
no. 2, 97-102.
- Lev69
-
D. A. Levine, Algorithm 344. Student's
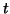 -distribution, Comm. ACM
12 (1969), 37-38, for remarks see same journal v. 13 (1970), pp.
124 and 449.
-distribution, Comm. ACM
12 (1969), 37-38, for remarks see same journal v. 13 (1970), pp.
124 and 449.
- Lew91
-
S. Lewanowicz, Evaluation of Bessel function integrals with algebraic
singularities, J. Comput. Appl. Math. 37 (1991), 101-112.
- LF94
-
Albrecht Lindner and Heino Freese, A new method to compute Mathieu
functions, J. Phys. A 27 (1994), no. 16, 5565-5571.
- LG64
-
H. Lotsch and M. Gray, Algorithm 244. Fresnel integrals, Comm. ACM
7 (1964), 660-661.
- Lin72
-
P. Linz, A method for computing Bessel function integrals, Math. Comp.
26 (1972), 509-513.
- Liu96
-
K. M. Liu, Numerical solution of Mathieu's differential equation with
the tau method, Southeast Asian Bull. Math. 20 (1996), no. 3,
59-63, Conference on Scientific Computation '94 (Shatin, 1994).
- LK73
-
P. Linz and T. E. Kropp, A note on the computation of integrals involving
products of trigonometric and Bessel functions, Math. Comp. 27
(1973), 871-872.
- LMS73a
-
D. W. Lozier, L. C. Maximon, and W. L. Sadowski, A bit comparison program
for algorithm testing, Comput. J. 16 (1973), 111-117.
- LMS73b
-
D. W. Lozier, L. C. Maximon, and W. L. Sadowski, Performance testing of a
Fortran library of mathematical function routines--A case study in the
application of testing techniques, J. Res. Nat. Bur. Standards 77B
(1973), 101-110.
- LO93
-
D. W. Lozier and F. W. J. Olver, Airy and Bessel functions by
parallel integration of ODEs, Proceedings of the Sixth SIAM Conference
on Parallel Processing for Scientific Computing, vol. 2 (R. F. Sincovec,
D. E. Keyes, M. R. Leuze, L. R. Petzold, and D. A. Reed, eds.), Society for
Industrial and Applied Mathematics, Philadelphia, 1993, pp. 531-538.
- LO94
-
D. W. Lozier and F. W. J. Olver, Numerical evaluation of special
functions, Mathematics of Computation 1943-1993: A Half-Century of
Computational Mathematics (W. Gautschi, ed.), Proceedings of Symposia in
Applied Mathematics, vol. 48, American Mathematical Society, Providence,
Rhode Island 02940, 1994, pp. 79-125. See also http://math.nist.gov/nesf/.
- LPM81
-
A. R. Lehman, W. C. Parke, and L. C. Maximon, Numerical evaluation of
integrals containing a spherical Bessel function by product integration,
J. Math. Phys. 22 (1981), 1399-1413.
- LPT80
-
M. C. Lorenzini, G. Puleo, and A. Tortorici Macaluso, Un package di
aritmetica in multiprecisione ed applicazione al calcolo dei polinomi di
Jacobi, Hermite, Laguerre, Legendre, Chebyshev, Atti Accad. Sci.
Lett. Arti Palermo Ser. 4, Parte 1 39 (1980), 339-376.
- LR74
-
W. P. Latham and R. W. Redding, On the calculation of the parabolic
cylinder functions, J. Comput. Phys. 16 (1974), 66-75.
- LS81
-
D. W. Lozier and J. M. Smith, Algorithm 567. Extended-range arithmetic
and normalized Legendre polynomials, ACM Trans. Math. Software 7
(1981), 141-146.
- LS91
-
A. I. Litvin and S. D. Simonzhenkov, Computation of Fermi-Dirac
functions, Comput. Math. Math. Phys. 31 (1991), no. 8, 100-103.
- LS95
-
S. K. Lucas and H. A. Stone, Evaluating infinite integrals involving
Bessel functions of arbitrary order, J. Comput. Appl. Math. 64
(1995), 217-231.
- Luc95
-
S. K. Lucas, Evaluating infinite integrals involving products of Bessel
functions of arbitrary order, J. Comput. Appl. Math. 64 (1995),
269-282.
- Luk68
-
Y. L. Luke, Approximations for elliptic integrals, Math. Comp.
22 (1968), 627-634.
- Luk69a
-
Y. L. Luke, The special functions and their approximations, vol. 1,
Academic Press, New York, 1969.
- Luk69b
-
Y. L. Luke, The special functions and their approximations, vol. 2,
Academic Press, New York, 1969.
- Luk70a
-
Y. L. Luke, Evaluation of the gamma function by means of Padé
approximations, SIAM J. Math. Anal. 1 (1970), 266-281.
- Luk70b
-
Y. L. Luke, Further approximations for elliptic integrals, Math. Comp.
24 (1970), 191-198.
- Luk71a
-
Y. L. Luke, Miniaturized tables of Bessel functions, Math. Comp.
25 (1971), 323-330.
- Luk71b
-
Y. L. Luke, Miniaturized tables of Bessel functions. II, Math. Comp.
25 (1971), 789-795, for corrigendum see same journal v. 26 (1972),
Microfiche Supplement A1-A7.
- Luk72a
-
Y. L. Luke, Miniaturized tables of Bessel functions. III, Math.
Comp. 26 (1972), 237-240, with Microfiche Supplement.
- Luk72b
-
Y. L. Luke, On generating Bessel functions by use of the backward
recurrence formula, Tech. Report ARL 72-0030, Aerospace Research
Laboratories, Wright-Patterson Air Force Base, Ohio, 1972.
- Luk75
-
Y. L. Luke, Mathematical functions and their approximations, Academic
Press, New York, 1975.
- Luk76
-
Y. L. Luke, On the expansion of exponential type integrals in series of
Chebyshev polynomials, Theory of Approximation with Applications (A. G.
Law and B. N. Sahney, eds.), Academic Press, Inc., New York, 1976,
pp. 180-199.
- Luk77a
-
Y. L. Luke, Algorithms for rational approximations for a confluent
hypergeometric function, Utilitas Math. 11 (1977), 123-151.
- Luk77b
-
Y. L. Luke, Algorithms for the computation of mathematical functions,
Academic Press, New York, 1977.
- Lun85
-
J. Lund, Bessel transforms and rational extrapolation, Numer. Math.
47 (1985), 1-14.
- LW90
-
F. G. Lether and P. R. Wenston, An algorithm for the numerical
computation of the Voigt function, Appl. Math. Comput. 35 (1990),
277-289.
- LW91
-
F. G. Lether and P. R. Wenston, The numerical computation of the Voigt
function by a corrected midpoint quadrature rule for
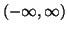 , J.
Comput. Appl. Math. 34 (1991), 75-92.
, J.
Comput. Appl. Math. 34 (1991), 75-92.
- LW95
-
F. G. Lether and P. R. Wenston, Minimax approximations to the zeros of
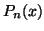 and Gauss-Legendre quadrature, J. Comput. Appl. Math.
59 (1995), 245-252.
and Gauss-Legendre quadrature, J. Comput. Appl. Math.
59 (1995), 245-252.
- LY88
-
T. Y. Lemczyk and M. M. Yovanovich, Efficient evaluation of incomplete
elliptic integrals and functions, Comput. Math. Appl. 16 (1988),
747-757.
- Lyn93
-
A. E. Lynas-Gray, VOIGTL--A fast subroutine for Voigt function
evaluation on vector processors, Comput. Phys. Comm. 75 (1993),
135-142.
- Mac89
-
A. J. MacLeod, Algorithm AS 245. A robust and reliable algorithm for
the logarithm of the gamma function, Appl. Statist. 38 (1989),
397-402.
- Mac93
-
A. J. MacLeod, Chebyshev expansions for modified Struve and related
functions, Math. Comp. 60 (1993), 735-747.
- Mac94a
-
Allan J. MacLeod, Computation of inhomogeneous Airy functions, J.
Comput. Appl. Math. 53 (1994), no. 1, 109-116.
- Mac94b
-
Allan J. MacLeod, Table-based tests for Bessel function software, Adv.
Comput. Math. 2 (1994), no. 2, 251-260.
- Mac96a
-
A. J. MacLeod, Algorithm 757: MISCFUN, a software package to compute
uncommon special functions, ACM Trans. Math. Software 22 (1996),
288-301.
- Mac96b
-
A. J. MacLeod, Rational approximations, software and test methods for
sine and cosine integrals, Numer. Algorithms 12 (1996), 259-272.
- Mac97
-
D. A. MacDonald, On the computation of zeroes of
 , Quart. Appl. Math. 55 (1997), no. 4, 623-633.
, Quart. Appl. Math. 55 (1997), no. 4, 623-633.
- Mac98
-
A. J. MacLeod, Algorithm 779. Fermi-Dirac functions of order
 ,
,
 ,
, 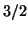 ,
, 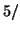 2, ACM Trans. Math. Software 24 (1998), 1-12.
2, ACM Trans. Math. Software 24 (1998), 1-12.
- Mar65
-
B. Markman, Contribution no. 14. The Riemann zeta function, BIT
5 (1965), 138-141.
- Mar82
-
A. L. Marshak, On the approximation of the exponential integral by
quadrature formulae, U.S.S.R. Comput. Math. and Math. Phys. 22
(1982), no. 5, 20-28.
- Mas83
-
J. P. Mason, Cylindrical Bessel functions for a large range of complex
arguments, Comput. Phys. Comm. 30 (1983), 1-11.
- Mat92
-
MATLAB high performance numeric computation and visualization software
reference guide, The MathWorks, Inc., Cochituate Place, 24 Prime Park Way,
Natick, Massachusetts 01760, August 1992, electronic mail address is
info@@mathworks.com.
- Mat93a
-
Mathcad 4.0 user's guide, MathSoft Inc., 201 Broadway, Cambridge,
Massachusetts 02139, March 1993.
- Mat93b
-
Gregory Matviyenko, On the evaluation of Bessel functions, Appl.
Comput. Harmon. Anal. 1 (1993), no. 1, 116-135.
- MB73a
-
K. L. Majumder and G. P. Bhattacharjee, Algorithm AS 63. The
incomplete beta integral, Appl. Statist. 22 (1973), 409-411, for
remark see same journal v. 26 (1977), pp. 111-114.
- MB73b
-
K. L. Majumder and G. P. Bhattacharjee, Algorithm AS 64. Inverse of
the incomplete beta function ratio, Appl. Statist. 22 (1973),
411-414, for remarks and corrections see same journal v. 26 (1977), pp.
111-114, v. 39 (1990), pp. 309-310, v. 40 (1991), p. 236.
- MBF94
-
P. Marksteiner, E. Badralexe, and A. J. Freeman, Neumann-type expansion
of Coulomb functions, J. Computational Phys. 111 (1994), 49-52.
- McC74
-
J. H. McCabe, A continued fraction expansion, with a truncation error
estimate, for Dawson's integral, Math. Comp. 28 (1974), 811-816.
- McC81
-
P. McCullagh, A rapidly convergent series for computing
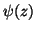 and
its derivatives, Math. Comp. 36 (1981), 247-248.
and
its derivatives, Math. Comp. 36 (1981), 247-248.
- MDS92
-
R. C. McPhedran, D. H. Dawes, and T. C. Scott, On a Bessel function
integral, Appl. Algebra Engrg. Comm. Comput. 2 (1992), no. 3,
207-216.
- MF86
-
V. P. Modenov and A. V. Filonov, Calculation of zeros of cylindrical
functions and their derivatives, Vestnik Moskov. Univ. Ser. XV Vychisl. Mat.
Kibernet. (1986), no. 2, 63-64, 71 (Russian).
- MF94
-
K. Mayrhofer and F. D. Fischer, Analytical solutions and a numerical
algorithm for the Gauss's hypergeometric function
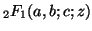 , Z. Angew. Math. Mech. 74 (1994), no. 7, 265-273.
, Z. Angew. Math. Mech. 74 (1994), no. 7, 265-273.
- MH73
-
T. Morita and T. Horiguchi, Convergence of arithmetic-geometric mean
procedure for the complex variables and the calculation of the complete
elliptic integrals with complex modulus, Numer. Math. 20 (1973),
425-430, for correction see same journal v. 29 (1978), pp. 233-236.
- Mid75
-
P. Midy, An improved calculation of the general elliptic integral of the
second kind in the neighbourhood of
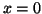 , Numer. Math. 25 (1975),
99-101.
, Numer. Math. 25 (1975),
99-101.
- MM90
-
P. Mali
 ký and M. Mali
ký and M. Mali ká, On the computation of
Riccati-Bessel functions, Apl. Mat. 35 (1990), 487-493.
ká, On the computation of
Riccati-Bessel functions, Apl. Mat. 35 (1990), 487-493.
- MMV81
-
G. Maino, E. Menapace, and A. Ventura, Computation of parabolic cylinder
functions by means of a Tricomi expansion, J. Comput. Phys. 40
(1981), 294-304.
- MN97
-
N. Mohankumar and A. Natarajan, The accurate evaluation of a particular
Fermi-Dirac integral, Comput. Phys. Comm. 101 (1997), 47-53.
- Moi88
-
A. I. Moiseyev, Computation of certain functions related to the Hurwitz
zeta-function, U.S.S.R. Comput. Math. and Math. Phys. 28 (1988),
no. 3, 1-6.
- Moo81
-
W. Moon, Airy function with complex arguments, Comput. Phys. Comm.
22 (1981), 411-417.
- Moo82
-
R. J. Moore, Algorithm AS 187. Derivatives of the incomplete gamma
integral, Appl. Statist. 31 (1982), 330-335.
- Moo83
-
D. R. Mook, An algorithm for the numerical evaluation of the Hankel and
Abel transforms, IEEE Trans. Acoust. Speech Signal Process. 31
(1983), 979-985.
- Mor69
-
J. Morris, Algorithm 346.
 -test probabilities, Comm. ACM
12 (1969), 184-185, for remark see ACM Trans. Math. Software v. 14
(1988), pp. 288-289.
-test probabilities, Comm. ACM
12 (1969), 184-185, for remark see ACM Trans. Math. Software v. 14
(1988), pp. 288-289.
- Mor79
-
R. Morris, The dilogarithm function of a real argument, Math. Comp.
33 (1979), 778-787.
- Mor80
-
M. Mori, Analytic representations suitable for numerical computation of
some special functions, Numer. Math. 35 (1980), 163-174.
- Mor83
-
M. Mori, A method for evaluation of the error function of real and
complex variable with high relative accuracy, Publ. Res. Inst. Math. Sci.
19 (1983), 1081-1094.
- Mor93
-
A. H. Morris, Jr., NSWC library of mathematics subroutines,
NSWCDD/TR-92/425, Naval Surface Warfare Center, Dahlgren Division,
Dahlgren, Virginia, 22448, January 1993.
- Mor96
-
Tohru Morita, Use of the Gauss contiguous relations in computing the
hypergeometric functions
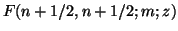 , Interdiscip. Inform. Sci.
2 (1996), no. 1, 63-74.
, Interdiscip. Inform. Sci.
2 (1996), no. 1, 63-74.
- Mor99
-
T. Morita, Calculation of the elliptic integrals of the first and second
kinds with complex modulus, Numer. Math. 82 (1999), 677-688.
- MOS66
-
W. Magnus, F. Oberhettinger, and R. P. Soni, Formulas and theorems for
the special functions of mathematical physics, Die Grundlehren der
mathematischen Wissenschaften in Einzeldarstellungen, vol. 52,
Springer-Verlag, New York, 1966.
- Mos89
-
S. L. B. Moshier, Methods and programs for mathematical functions, Ellis
Horwood Limited, Chichester, 1989, separate diskette. Programs downloadable
from Netlib and GAMS.
- MR71
-
F. Matta and A. Reichel, Uniform computation of the error function and
other related functions, Math. Comp. 25 (1971), 339-344.
- MY91
-
P. Midy and Y. Yakovlev, Computing some elementary functions of a complex
variable, Math. Comput. Simulation 33 (1991), 33-49.
- NAG99
-
NAG Fortran library manual, mark 19, vol. 10, NAG Inc., 1400 Opus
Place, Suite 200, Downers Grove, Illinois 60515-5702, June 1999.
- NC66
-
W. J. Nellis and B. C. Carlson, Reduction and evaluation of elliptic
integrals, Math. Comp. 20 (1966), 223-231.
- NDT69
-
E. W. Ng, C. J. Devine, and R. F. Tooper, Chebyshev polynomial expansion
of Bose-Einstein functions of orders 1 to 10, Math. Comp. 23
(1969), 639-643.
- Ném65
-
G. Németh, Chebyshev expansions for Fresnel Integrals, Numer.
Math. 7 (1965), 310-312.
- Ném92
-
G. Németh, Mathematical approximation of special functions: Ten
papers on Chebyshev expansions, Nova Science Publishers Inc., Commack, NY,
1992.
- Nes84
-
R. K. Nesbet, Algorithms for regular and irregular Coulomb and Bessel
functions, Comput. Phys. Comm. 32 (1984), 341-347.
- New84
-
J. N. Newman, Approximations for the Bessel and Struve functions,
Math. Comp. 43 (1984), 551-556.
- Ng75
-
E. W. Ng, A comparison of computational methods and algorithms for the
complex gamma function, ACM Trans. Math. Software 1 (1975), 56-70.
- NM93
-
A. Natarajan and N. Mohan Kumar, On the numerical evaluation of the
generalised Fermi-Dirac integrals, Comput. Phys. Comm. 76
(1993), 48-50.
- NPB92a
-
M. Nardin, W. F. Perger, and A. Bhalla, Algorithm 707. CONHYP: A
numerical evaluator of the confluent hypergeometric function for complex
arguments of large magnitudes, ACM Trans. Math. Software 18 (1992),
345-349.
- NPB92b
-
M. Nardin, W. F. Perger, and A. Bhalla, Numerical evaluation of the
confluent hypergeometric function for complex arguments of large magnitudes,
J. Comput. Appl. Math. 39 (1992), 193-200.
- NT84
-
C. J. Noble and I. J. Thompson, COULN, a program for evaluating
negative energy Coulomb functions, Comput. Phys. Comm. 33 (1984),
413-419.
- OFM78
-
A. V. Oppenheim, G. V. Frisk, and D. R. Martinez, An algorithm for the
numerical evaluation of the Hankel transform, Proc. Inst. Electr.
Electron. Engrg. 66 (1978), 264-265.
- Olv74
-
F. W. J. Olver, Asymptotics and special functions, Academic Press, New
York, 1974.
- Olv91
-
F. W. J. Olver, Review of United Laboratories, Inc., Mathematical
Function Library for Microsoft-Fortran, Wiley, New York, 1989,
Math. Comp. 56 (1991), 879-885.
- OM68
-
D. Osborn and R. Madey, The incomplete beta function and its ratio to the
complete beta function, Math. Comp. 22 (1968), 159-162.
- Öpi87
-
U. Öpik, A program to set up systems of orthogonal polynomials,
Comput. Phys. Comm. 46 (1987), 263-296.
- OPP95
-
C. Osácar, J. Palacián, and M. Palacios, Numerical evaluation of
the dilogarithm of complex argument, Celestial Mech. Dynam. Astronom.
62 (1995), no. 1, 93-98.
- OS72
-
F. W. J. Olver and D. J. Sookne, Note on backward recurrence algorithms,
Math. Comp. 26 (1972), 941-947.
- OS83
-
F. W. J. Olver and J. M. Smith, Associated Legendre functions on the
cut, J. Comput. Phys. 51 (1983), 502-518.
- PA92
-
C. U. Pabon-Ortiz and M. Artoni, Laguerre polynomials: Novel
properties and numerical generation scheme for analysis of a discrete
probability distribution, Comput. Phys. Comm. 71 (1992), 215-221.
- PA99
-
A. Poquérusse and S. Alexiou, Fast analytic formulas for the modified
Bessel functions of imaginary order for spectral line broadening
calculations, J. Quant. Spectr. Rad. Trans. 62 (1999), 389-395.
- Pac70
-
K. A. Paciorek, Algorithm 385. Exponential integral
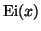 , Comm. ACM 13 (1970), 446-447, for
certification and remarks see same journal v. 13 (1970), pp. 448-449 and p.
750; v. 15 (1972), p. 1074.
, Comm. ACM 13 (1970), 446-447, for
certification and remarks see same journal v. 13 (1970), pp. 448-449 and p.
750; v. 15 (1972), p. 1074.
- Pal69
-
A. A. Pal'cev, The computation of spheroidal functions and their first
derivatives on a computer. I, Vesc
 Akad. Navuk BSSR Ser.
F
Akad. Navuk BSSR Ser.
F z.-Mat. Navuk (1969), no. 1, 19-25 (Russian).
z.-Mat. Navuk (1969), no. 1, 19-25 (Russian).
- Pas88
-
S. Paszkowski, Evaluation of Fermi-Dirac integral, Nonlinear
Numerical Methods and Rational Approximation (A. Cuyt, ed.), D. Reidel
Publishing Company, Dordrecht, 1988, pp. 435-444.
- Pas91
-
S. Paszkowski, Evaluation of the Fermi-Dirac integral of half-integer
order, Zastos. Mat. 21 (1991), 289-301.
- Pas95
-
S. Paszkowski, Quasipower and hypergeometric series--construction and
evaluation, Numer. Algorithms 10 (1995), 337-361.
- PB72
-
R. Piessens and M. Branders, Chebyshev polynomial expansions of the
Riemann zeta function, Math. Comp. 26 (1972), 1022.
- PB82
-
R. Piessens and M. Branders, Approximation for Bessel functions and
their application in the computation of Hankel transforms, Comput. Math.
Appl. 8 (1982), 305-311.
- PB83
-
R. Piessens and M. Branders, Modified Clenshaw-Curtis method for the
computation of Bessel function integrals, BIT 23 (1983),
370-381.
- PB84
-
R. Piessens and M. Branders, Algorithm 28. Algorithm for the
computation of Bessel function integrals, J. Comput. Appl. Math.
11 (1984), 119-137.
- PB85
-
R. Piessens and M. Branders, A survey of numerical methods for the
computation of Bessel function integrals, Rend. Sem. Mat. Univ. Politec.
Torino Fascicolo Speciale. Special Functions: Theory and Computation
(1985), 249-265.
- PBN93
-
W. F. Perger, A. Bhalla, and M. Nardin, A numerical evaluator for the
generalized hypergeometric series, Comput. Phys. Comm. 77 (1993),
249-254.
- PDK96
-
S. D. Panteliou, A. D. Dimarogonas, and I. N. Katz, Direct and inverse
interpolation for Jacobian elliptic functions, zeta function of Jacobi
and complete elliptic integrals of the second kind, Comput. Math. Appl.
32 (1996), no. 8, 51-57.
- PDL93
-
Brian A. Pettitt, Werner Danchura, and Donna Labun, Spherical Bessel
transforms, J. Comput. Phys. 105 (1993), no. 1, 178-181.
- Pea22
-
K. Pearson, Tables of the incomplete
 -function, H. M.
Stationery Office, London, 1922, reissued by Biometrika, 1934.
-function, H. M.
Stationery Office, London, 1922, reissued by Biometrika, 1934.
- Pex70
-
R. L. Pexton, Computer investigation of Coulomb wave functions, Math.
Comp. 24 (1970), 409-411.
- Phi88
-
H. N. Phien, A Fortran routine for the computation of gamma
percentiles, Adv. Eng. Software 10 (1988), 159-164.
- Phi90
-
H. N. Phien, A note on the computation of the incomplete beta function,
Adv. Eng. Software 12 (1990), 39-44.
- Pic89
-
B. Pichon, Numerical calculation of the generalized Fermi-Dirac
integrals, Comput. Phys. Comm. 55 (1989), 127-136.
- Pie82
-
R. Piessens, Automatic computation of Bessel function integrals,
Comput. Phys. Comm. 25 (1982), 289-295.
- Pie84a
-
R. Piessens, Chebyshev series approximations for the zeros of the
Bessel functions, J. Comput. Phys. 53 (1984), 188-192.
- Pie84b
-
R. Piessens, The computation of Bessel functions on a small computer,
Comput. Math. Appl. 10 (1984), 161-166.
- Pie90
-
R. Piessens, On the computation of zeros and turning points of Bessel
functions, Bull. Soc. Math. Grèce (N.S.) 31 (1990), 117-122.
- Pri75
-
P. J. Prince, Algorithm 498. Airy functions using Chebyshev series
approximations, ACM Trans. Math. Software 1 (1975), 372-379.
- PT84
-
B. A. Popov and G. S. Tesler, Computation of functions on electronic
computers--handbook, Naukova Dumka, Kiev, 1984 (Russian), see review by K.
S. Kölbig in Math. Comp. v. 55 (1990), pp. 395-397.
- PT90
-
W. H. Press and S. A. Teukolsky, Elliptic integrals, Comput. in Phys.
4 (1990), Jan/Feb, 92-96.
- PTVF92
-
W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery,
Numerical recipes in Fortran 77. The art of scientific computing,
second ed., Cambridge University Press, 1992., Reprinted with corrections
in 1997. Diskettes and example books available. Editions exist in Basic
(1991), C (1992), Fortran (1992), Macintosh Fortran (1988) and Pascal (1989).
- Puo88
-
M. Puoskari, A method for computing Bessel function integrals, J.
Comput. Phys. 75 (1988), 334-344.
- PW90a
-
G. P. M. Poppe and C. M. J. Wijers, Algorithm 680. Evaluation of the
complex error function, ACM Trans. Math. Software 16 (1990), 47.
- PW90b
-
G. P. M. Poppe and C. M. J. Wijers, More efficient computation of the
complex error function, ACM Trans. Math. Software 16 (1990),
38-46.
- RBMW59
-
M. Rotenberg, R. Bivins, N. Metropolis, and J. K. Wooten, Jr., The 3-j
and 6-j symbols, The Technology Press, Massachusetts Institute of
Technology, Cambridge, Massachusetts, 1959.
- Rem73
-
G. F. Remenets, Computation of Hankel (Bessel) functions
of complex index and argument by numerical integration of a Schläfli
contour integral, U.S.S.R. Comput. Math. and Math. Phys. 13 (1973),
no. 6, 58-67.
- Ren96
-
O. Renault, A new algorithm for computing orthogonal polynomials, J.
Comput. Appl. Math. 75 (1996), 231-248.
- RF93
-
Yu. L. Ratis and P. Fernández de Córdoba, A code to
calculate (high order) Bessel functions based on the continued
fractions method, Comput. Phys. Comm. 76 (1993), 381-388.
- RH84
-
J. R. Rice and R. J. Hanson, Algorithm 620. References and keywords for
collected algorithms from ACM, ACM Trans. Math. Software 10
(1984), 359-360.
- Ric83
-
J. R. Rice, Numerical methods, software and analysis: IMSL reference
edition, McGraw-Hill Book Company, New York, 1983.
- Riv90
-
T. J. Rivlin, Chebyshev polynomials. From approximation theory to
algebra and number theory, second ed., John Wiley and Sons, Inc., New York,
1990.
- RL76
-
R. W. Redding and W. P. Latham, On the calculation of the parabolic
cylinder functions. II. The function
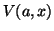 , J. Comput. Phys.
20 (1976), 256-258.
, J. Comput. Phys.
20 (1976), 256-258.
- RL80
-
S. R. Rengarajan and J. E. Lewis, Mathieu functions of integral orders
and real arguments, IEEE Trans. Microwave Theory Tech. 28 (1980),
276-277.
- RP96
-
V. Mohammad Raffee and C. L. Parihar, Computational method for the
hypergeometric function
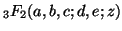 , J. Maulana Azad
College Tech. 29 (1996), 87-99.
, J. Maulana Azad
College Tech. 29 (1996), 87-99.
- RS81
-
M. Razaz and J. L. Schonfelder, Remark on Algorithm 498. Airy
functions using Chebyshev series approximations, ACM Trans. Math. Software
7 (1981), 404-405.
- RWGH87
-
J. P. Royston, J. B. Webb, P. Griffiths, and I. D. Hill, The construction
and description of algorithms, Appl. Statist. 36 (1987), 94-103.
- Ryb89
-
G. B. Rybicki, Dawson's integral and the sampling theorem, Comput. in
Phys. 3 (1989), Mar/Apr, 85-87.
- SAG79
-
Z. Schulten, D. G. M. Anderson, and R. G. Gordon, An algorithm for the
evaluation of the complex Airy functions, J. Comput. Phys. 31
(1979), 60-75.
- Sag91a
-
R. P. Sagar, A Gaussian quadrature for the calculation of generalized
Fermi-Dirac integrals, Comput. Phys. Comm. 66 (1991), 271-275.
- Sag91b
-
R. P. Sagar, On the evaluation of the Fermi-Dirac integrals,
Astrophys. J. 376 (1991), 364-366.
- Sal89
-
K. L. Sala, Transformations of the Jacobian amplitude function and its
calculation via the arithmetic-geometric mean, SIAM J. Math. Anal.
20 (1989), 1514-1528.
- SBK92
-
O. A. Sharafeddin, H. F. Bowen, and D. J. Kouri, Numerical evaluation of
spherical Bessel transforms via fast Fourier transforms, J. Comput.
Phys. 100 (1992), 294-296.
- Sch74
-
B. Schorr, Programs for the Landau and the Vavilov distributions and
the corresponding random numbers, Comput. Phys. Comm. 7 (1974),
215-224.
- Sch76
-
J. L. Schonfelder, The production of special function routines for a
multi-machine library, Software--Practice and Experience 6 (1976),
71-82.
- Sch78
-
J. L. Schonfelder, Chebyshev expansions for the error and related
functions, Math. Comp. 32 (1978), 1232-1240.
- Sea82
-
M. J. Seaton, Coulomb functions analytic in the energy, Comput. Phys.
Comm. 25 (1982), 87-95.
- Sec99
-
J. D. Secada, Numerical evaluation of the Hankel transform, Comput.
Phys. Comm. 116 (1999), 278-294.
- Seg98
-
J. Segura, A global Newton method for the zeros of cylinder functions,
Numer. Algorithms 18 (1998), 259-276.
- SFR97
-
J. Segura, P. Fernández de Córdoba, and Yu. L. Ratis, A code to
evaluate modified Bessel functions based on the continued fraction method,
Comput. Phys. Comm. 105 (1997), no. 2-3, 263-272.
- SG72
-
A. J. Strecok and J. A. Gregory, High precision evaluation of the
irregular Coulomb wave functions, Math. Comp. 26 (1972),
955-961.
- SG98
-
J. Segura and A. Gil, Parabolic cylinder functions of integer and
half-integer orders for nonnegative arguments, Comput. Phys. Comm.
115 (1998), 69-86.
- SGA81
-
Z. Schulten, R. G. Gordon, and D. G. M. Anderson, A numerical algorithm
for the evaluation of Weber parabolic cylinder functions
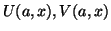 , and
, and
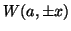 , J. Comput. Phys. 42 (1981),
213-237.
, J. Comput. Phys. 42 (1981),
213-237.
- She74
-
V. B. Sheorey, Chebyshev expansions for wave functions, Comput. Phys.
Comm. 7 (1974), 1-12.
- She88
-
B. L. Shea, Algorithm AS 239. Chi-squared and incomplete gamma
integral, Appl. Statist. 37 (1988), 466-473.
- Shi93a
-
R. B. Shirts, Algorithm 721. MTIEU1 and MTIEU2: Two subroutines to
compute eigenvalues and solutions to Mathieu's differential equation for
noninteger and integer order, ACM Trans. Math. Software 19 (1993),
391-406.
- Shi93b
-
R. B. Shirts, The computation of eigenvalues and solutions of Mathieu's
differential equation for noninteger order, ACM Trans. Math. Software
19 (1993), 377-390.
- Sid97
-
A. Sidi, Computation of infinite integrals involving Bessel functions
of arbitrary order by the
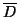 -transformation, J. Comput. Appl.
Math. 78 (1997), 125-130.
-transformation, J. Comput. Appl.
Math. 78 (1997), 125-130.
- Sie77
-
A. E. Siegman, Quasi fast Hankel transform, Optics Lett. 1
(1977), 13-15.
- Sim64
-
J. M. S. Simões Pereira, Algorithm 234. Poisson-Charlier
polynomials, Comm. ACM 7 (1964), 420, for certification see same
journal v. 8 (1965), p. 105.
- SJ96
-
P. N. Shivakumar and Chuanxiang Ji, Upper and lower bounds for inverse
elements of finite and infinite tridiagonal matrices, Linear Algebra Appl.
247 (1996), 297-316.
- Sko85
-
S. L. Skorokhodov, On the computation of complex zeros of the modified
Bessel function of the second kind, Soviet Math. Dokl. 31 (1985),
78-81.
- SL73
-
W. L. Sadowski and D. W. Lozier, A unified standards approach to
algorithm testing, Program Test Methods (W. C. Hetzel, ed.),
Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1973, pp. 277-290.
- SL81
-
M. M. Shepherd and J. G. Laframboise, Chebyshev approximation of
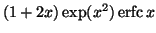 in
in
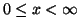 , Math. Comp. 36 (1981), 249-253.
, Math. Comp. 36 (1981), 249-253.
- SM75
-
B. P. Sinha and R. H. MacPhie, On the computation of the prolate
spheroidal radial functions of the second kind, J. Math. Phys. 16
(1975), 2378-2381.
- Smi89
-
D. M. Smith, Efficient multiple-precision evaluation of elementary
functions, Math. Comp. 52 (1989), 131-134.
- Smi91
-
D. M. Smith, Algorithm 693. A Fortran package for floating-point
multiple-precision arithmetic, ACM Trans. Math. Software 17 (1991),
273-283.
- Sny93
-
W. V. Snyder, Algorithm 723. Fresnel integrals, ACM Trans. Math.
Software 19 (1993), 452-456, for remark see same journal v. 22
(1996), pp. 498-500.
- SO87
-
J. Spanier and K. B. Oldham, An atlas of functions, Hemisphere
Publishing Corporation, Washington, D. C., 1987.
- SOL81
-
J. M. Smith, F. W. J. Olver, and D. W. Lozier, Extended-range arithmetic
and normalized Legendre polynomials, ACM Trans. Math. Software 7
(1981), 93-105.
- SP75
-
P. Spellucci and P. Pulay, Effective calculation of the incomplete gamma
function for parameter values
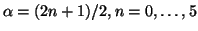 , Angew.
Informatik 17 (1975), 30-32.
, Angew.
Informatik 17 (1975), 30-32.
- Spo94
-
John L. Spouge, Computation of the gamma, digamma, and trigamma
functions, SIAM J. Numer. Anal. 31 (1994), no. 3, 931-944.
- Spr91
-
J. C. Sprott, Numerical recipes: Routines and examples in BASIC,
Cambridge University Press, 1991.
- Str68
-
A. J. Strecok, On the calculation of the inverse of the error function,
Math. Comp. 22 (1968), 144-158.
- Sym92
-
MACSYMA reference manual, version 13, Symbolics, Inc., 20 Academy St.,
Arlington, Massachusetts 02174-6436, November 1992.
- SZ70
-
I. A. Stegun and R. Zucker, Automatic computing methods for special
functions, J. Res. Nat. Bur. Standards 74B (1970), 211-224.
- SZ74
-
I. A. Stegun and R. Zucker, Automatic computing methods for special
functions. Part II. The exponential integral
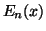 , J. Res. Nat.
Bur. Standards 78B (1974), 199-216.
, J. Res. Nat.
Bur. Standards 78B (1974), 199-216.
- SZ76
-
I. A. Stegun and R. Zucker, Automatic computing methods for special
functions. Part III. The sine, cosine, exponential integrals, and
related functions, J. Res. Nat. Bur. Standards 80B (1976),
291-311.
- SZ79
-
B. Sommer and J. G. Zabolitzky, On numerical Bessel transformation,
Comput. Phys. Comm. 16 (1979), 383-387.
- SZ81
-
I. A. Stegun and R. Zucker, Automatic computing methods for special
functions. Part IV. Complex error function, Fresnel integrals, and
other related functions, J. Res. Nat. Bur. Standards 86 (1981),
661-686.
- Tal83
-
J. D. Talman, LSFBTR: A subroutine for calculating spherical Bessel
transforms, Comput. Phys. Comm. 30 (1983), 93-99.
- Tau92
-
G. Taubmann, Parabolic cylinder functions
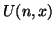 for natural
for natural  and
positive
and
positive 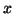 , Comput. Phys. Comm. 69 (1992), 415-419.
, Comput. Phys. Comm. 69 (1992), 415-419.
- TB85
-
I. J. Thompson and A. R. Barnett, COULCC: A continued-fraction
algorithm for Coulomb functions of complex order with complex arguments,
Comput. Phys. Comm. 36 (1985), 363-372.
- TB86
-
I. J. Thompson and A. R. Barnett, Coulomb and Bessel functions of
complex arguments and order, J. Comput. Phys. 64 (1986), 490-509.
- TB87
-
I. J. Thompson and A. R. Barnett, Modified Bessel functions
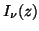 and
and
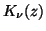 of real order and complex argument, to
selected accuracy, Comput. Phys. Comm. 47 (1987), 245-257.
of real order and complex argument, to
selected accuracy, Comput. Phys. Comm. 47 (1987), 245-257.
- Tem75
-
N. M. Temme, On the numerical evaluation of the modified Bessel
function of the third kind, J. Comput. Phys. 19 (1975), 324-337.
- Tem76
-
N. M. Temme, On the numerical evaluation of the ordinary Bessel
function of the second kind, J. Comput. Phys. 21 (1976), 343-350.
- Tem77
-
N. M. Temme, The numerical computation of special functions by use of
quadrature rules for saddle point integrals. I. Trapezoidal integration
rules, Tech. Report TW 164/77, Mathematisch Centrum, Amsterdam, 1977.
- Tem78
-
N. M. Temme, Some aspects of applied analysis: Asymptotics, special
functions and their numerical computation, Mathematisch Centrum, Amsterdam,
1978.
- Tem79
-
N. M. Temme, An algorithm with ALGOL 60 program for the computation of
the zeros of ordinary Bessel functions and those of their derivatives, J.
Comput. Phys. 32 (1979), 270-279.
- Tem83
-
N. M. Temme, The numerical computation of the confluent hypergeometric
function
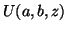 , Numer. Math. 41 (1983), 63-82.
, Numer. Math. 41 (1983), 63-82.
- Tem85
-
N. M. Temme, Special functions as approximants in uniform asymptotic
expansions of integrals; a survey, Rend. Sem. Mat. Univ. Politec.
Torino Fascicolo Speciale. Special Functions: Theory and Computation
(1985), 289-317.
- Tem87
-
N. M. Temme, On the computation of the incomplete gamma functions for
large values of the parameters, Inst. Math. Appl. Conf. Ser. New Ser., vol.
10: Algorithms for Approximation (Shrivenham, 1985), Oxford Univ. Press,
New York, 1987, pp. 479-489.
- Tem92a
-
N. M. Temme, Asymptotic inversion of incomplete gamma functions, Math.
Comp. 58 (1992), 755-764.
- Tem92b
-
N. M. Temme, Asymptotic inversion of the incomplete beta function, J.
Comput. Appl. Math. 41 (1992), 145-157.
- Tem94a
-
N. M. Temme, Computational aspects of incomplete gamma functions with
large complex parameters, Approximation and computation (West Lafayette, IN,
1993), Birkhäuser Boston, Boston, MA, 1994, pp. 551-562.
- Tem94b
-
N. M. Temme, A set of algorithms for the incomplete gamma functions,
Probab. Engrg. Inform. Sci. 8 (1994), 291-307.
- Tem95
-
N. M. Temme, Asymptotics of zeros of incomplete gamma functions, Ann.
Numer. Math. 2 (1995), 415-423.
- Tho97
-
W. J. Thompson, Atlas for computing mathematical functions: an
illustrated guide for practitioners, with programs in C and Mathematica,
John Wiley & Sons Inc., New York, 1997, Includes CD-ROM. Fortran 90
edition exists also.
- TM68
-
R. F. Tooper and J. Mark, Simplified calculation of
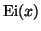 for positive arguments, and a short table of
for positive arguments, and a short table of
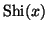 , Math. Comp. 22 (1968), 448-449.
, Math. Comp. 22 (1968), 448-449.
- TP83
-
N. Tu
 bay and E. Panayirci, An efficient algorithm for generation of
prolate spheroidal wave functions, Bull. Tech. Univ. Istanbul 36
(1983), 563-577.
bay and E. Panayirci, An efficient algorithm for generation of
prolate spheroidal wave functions, Bull. Tech. Univ. Istanbul 36
(1983), 563-577.
- TR69
-
T. Tamura and F. Rybicki, Coulomb functions for complex energies,
Comput. Phys. Comm. 1 (1969), 25-30, for erratum see same journal
v. 3 (1972), p. 276.
- ULI90
-
Mathematical function library for Microsoft-C, United Laboratories,
Inc., John Wiley & Sons, 1990, includes diskettes. Edition also exists in
Fortran (1989).
- Upo92
-
Ya. I. Upor, Calculation of zeros of orthogonal polynomials, Tbiliss.
Gos. Univ. Inst. Prikl. Mat. Trudy 44 (1992), 110-127, 222.
- vBBH70
-
A. L. van Buren, R. V. Baier, and S. Hanish, A Fortran computer program
for calculating the oblate spheroidal radial functions of the first and
second kind and their first derivatives, NRL Report No. 6959, Naval Res.
Lab., Washington, D. C., 1970.
- vBBHK72
-
A. L. van Buren, R. V. Baier, S. Hanish, and B. J. King, Calculation of
spheroidal wave functions, J. Acoust. Soc. Amer. 51 (1972),
414-416.
- vdLT84
-
C. G. van der Laan and N. M. Temme, Calculation of special functions:
The gamma function, the exponential integrals and error-like functions,
CWI Tract, vol. 10, Centrum voor Wiskunde en Informatica, Amsterdam, 1984.
- VGK+91
-
V. K. Vlasov, M. N. Glukhova, L. N. Korolev, M. S. Pelina, S. N.
Razumovski
 , and O. L. Ulasik, On the calculation of Bessel
functions of a complex index and a complex argument, Vestnik Moskov. Univ.
Ser. XV Vychisl. Mat. Kibernet. (1991), no. 3, 46-51, 64 (Russian).
, and O. L. Ulasik, On the calculation of Bessel
functions of a complex index and a complex argument, Vestnik Moskov. Univ.
Ser. XV Vychisl. Mat. Kibernet. (1991), no. 3, 46-51, 64 (Russian).
- VGK+92
-
V. K. Vlasov, M. N. Glukhova, L. N. Korolev, S. N. Razumovski
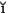 , and O. L.
Ulasik, On the calculation of the Mathieu functions, Vestnik Moskov.
Univ. Ser. XV Vychisl. Mat. Kibernet. 1992 (1992), no. 1, 65-69.
, and O. L.
Ulasik, On the calculation of the Mathieu functions, Vestnik Moskov.
Univ. Ser. XV Vychisl. Mat. Kibernet. 1992 (1992), no. 1, 65-69.
- VGRZ97
-
M. N. Vrahatis, T. N. Grapsa, O. Ragos, and F. A. Zafiropoulos, On the
localization and computation of zeros of Bessel functions, Z. Angew. Math.
Mech. 77 (1997), no. 6, 467-475.
- VRS+95
-
M. N. Vrahatis, O. Ragos, T. Skiniotis, F. A. Zafiropoulos, and T. N. Grapsa,
RFSFNS: A portable package for the numerical determination of the
number and the calculation of roots of Bessel functions, Comput. Phys.
Comm. 92 (1995), 252-266, for corrections see same journal v. 117
(1990), p. 290.
- VRS+97
-
M. N. Vrahatis, O. Ragos, T. Skiniotis, F. A. Zafiropoulos, and T. N. Grapsa,
The topological degree theory for the localization and computation of
complex zeros of Bessel functions, Numer. Funct. Anal. Optim. 18
(1997), no. 1-2, 227-234.
- VRZG96
-
M. N. Vrahatis, O. Ragos, F. A. Zafiropoulos, and T. N. Grapsa, Locating
and computing zeros of Airy functions, Z. Angew. Math. Mech. 76
(1996), no. 7, 419-422.
- vVNZ94
-
M. van Veldhuizen, R. Nieuwenhuizen, and W. Zijl, A note on log scale
Hankel transforms, J. Computational Phys. 110 (1994), 196-199.
- Wal84
-
J. L. Walmsley, On the efficient evaluation of modified Bessel
functions of zeroth and first orders for arguments of the form
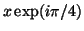 , J. Comput. Phys. 56 (1984), 349-355.
, J. Comput. Phys. 56 (1984), 349-355.
- War60
-
M. Ward, The calculation of the complete elliptic integral of the third
kind, Amer. Math. Monthly 67 (1960), 205-213.
- WBR82
-
C. A. Wills, J. M. Blair, and P. L. Ragde, Rational Chebyshev
approximations for the Bessel functions
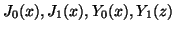 , Math. Comp. 39 (1982), 617-623.
, Math. Comp. 39 (1982), 617-623.
- WC90
-
E. J. Weniger and J. Ci
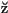 ek, Rational approximations for the modified
Bessel function of the second kind, Comput. Phys. Comm. 59
(1990), 471-493.
ek, Rational approximations for the modified
Bessel function of the second kind, Comput. Phys. Comm. 59
(1990), 471-493.
- Wei94a
-
J. A. C. Weideman, Computation of the complex error function, SIAM J.
Numer. Anal. 31 (1994), no. 5, 1497-1518, for correction see same
journal v. 32 (1995), pp.330-331.
- Wei94b
-
J. A. C. Weideman, Computing integrals of the complex error function,
These proceedings, 1994.
- WFQ92
-
Xi Liang Wang, Yong Cheng Feng, and Xian Ming Qing, Numerical computation
of cylindrical functions for complex arguments, Dianzi Keji Daxue Xuebao
21 (1992), no. 2, 152-157.
- Wie99
-
T. Wieder, Algorithm 794. Numerical Hankel transform by the Fortran
program HANKEL, ACM Trans. Math. Software 25 (1999), 240-250.
- Wim74
-
J. Wimp, On the computation of Tricomi's
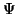 function, Computing
13 (1974), 195-203.
function, Computing
13 (1974), 195-203.
- Wim84
-
J. Wimp, Computation with recurrence relations, Pitman, London, 1984.
- Wit68
-
B. F. W. Witte, Algorithm 332. Jacobi polynomials, Comm. ACM
11 (1968), 436-437, for remarks see same journal v. 13 (1970), p.
449 and v. 18 (1975), pp. 116-117.
- WMC97
-
J. Wimp, P. McCabe, and J. N. L. Connor, Computation of Jacobi
functions of the second kind for use in nearside-farside scattering theory,
J. Comput. Appl. Math. 82 (1997), 447-464.
- WNO94
-
T. Watanabe, M. Natoni, and T. Oguni (eds.), Mathematical software for
the P.C. and workstations: A collection of Fortran 77 programs,
Elsevier Science B.V., North-Holland, Amsterdam, 1994, includes diskette.
- Wol99
-
S. Wolfram, The Mathematica book, fourth ed., Cambridge University
Press, 1999, see also http://documents.wolfram.com/v4/.
- Won89
-
R. Wong, Asymptotic approximations of integrals, Academic Press, New
York, 1989.
- Woo67
-
V. E. Wood, Chebyshev expansions for integrals of the error function,
Math. Comp. 21 (1967), 494-496.
- YKK88
-
A. Yu. Yeremin, I. E. Kaporin, and M. K. Kerimov, Computation of the
derivatives of the Riemann zeta-function in the complex domain, U.S.S.R.
Comput. Math. and Math. Phys. 28 (1988), no. 4, 115-124, see also
[EKK85].
- YM97
-
H. A. Yousif and R. Melka, Bessel function of the first kind with
complex argument, Comput. Phys. Comm. 106 (1997), 199-206.
- YN74
-
T. Yoshida and I. Ninomiya, Computation of Bessel functions
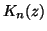 with complex argument by
with complex argument by 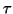 -method, J. Inform. Process. 14
(1974), 32-37.
-method, J. Inform. Process. 14
(1974), 32-37.
- Yos92
-
T. Yoshida, Error analysis of the recurrence technique for calculation of
Bessel functions
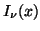 , J. Inform. Process. 15 (1992),
213-221.
, J. Inform. Process. 15 (1992),
213-221.
- Yos95
-
Toshio Yoshida, Computation of Kummer functions
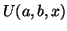 for large
argument
for large
argument 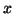 by using the
by using the 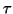 -method, Trans. Inform. Process. Soc. Japan
36 (1995), no. 10, 2335-2342.
-method, Trans. Inform. Process. Soc. Japan
36 (1995), no. 10, 2335-2342.
- Zan75
-
R. Zanovello, Sul calcolo numerico della funzione di Struve
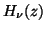 , Rend. Sem. Mat. Univ. Politec. Torino 32 (1975),
251-269.
, Rend. Sem. Mat. Univ. Politec. Torino 32 (1975),
251-269.
- ZB95
-
J. Zhang and J. A. Belward, Tau-method approximations for the Bessel
function
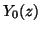 , Comput. Math. Appl. 30 (1995), no. 7, 5-14.
, Comput. Math. Appl. 30 (1995), no. 7, 5-14.
- ZB97
-
Jun Zhang and John A. Belward, Chebyshev series approximations for the
Bessel function
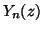 of complex argument, Appl. Math. Comput.
88 (1997), no. 2-3, 275-286.
of complex argument, Appl. Math. Comput.
88 (1997), no. 2-3, 275-286.
- ZGRV96
-
F. A. Zafiropoulos, T. N. Grapsa, O. Ragos, and M. N. Vrahatis, On the
computation of zeros of Bessel and Bessel-related functions, Proceedings
of the Sixth International Colloquium on Differential Equations (Plovdiv,
1995) (Utrecht), VSP, 1996, pp. 409-416.
- Zha95
-
J. Zhang, Tau-method approximations for the Bessel function
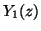 , Comput. Math. Appl. 30 (1995), no. 7, 15-19.
, Comput. Math. Appl. 30 (1995), no. 7, 15-19.
- Zha96a
-
J. Zhang, A note on the tau-method approximations for the Bessel
functions
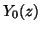 and
and
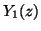 , Comput. Math. Appl. 31
(1996), no. 9, 63-70.
, Comput. Math. Appl. 31
(1996), no. 9, 63-70.
- Zha96b
-
J. Zhang, Symbolic and numerical computation on Bessel functions of
complex argument and large magnitude, J. Comput. Appl. Math. 75
(1996), 99-118.
- Ziv91
-
A. Ziv, Fast evaluation of elementary mathematical functions with
correctly rounded last bit, ACM Trans. Math. Software 17 (1991),
410-423.
- ZJ96
-
S. Zhang and J. Jin, Computation of special functions, John Wiley &
Sons Inc., New York, 1996, Includes diskette with Fortran programs.
- ZK95
-
Ya. M. Zhile
 kin and A. B. Kukarkin, A fast Fourier-Bessel
transformation algorithm, Comput. Math. Math. Phys. 35 (1995),
no. 7, 901-905.
kin and A. B. Kukarkin, A fast Fourier-Bessel
transformation algorithm, Comput. Math. Math. Phys. 35 (1995),
no. 7, 901-905.
Thursday, Jan 11, 2001