Parallel Cooperative Algorithms for Protein Folding

John Moult ([email protected])
Jan T. Pedersen ([email protected])

The elucidation of protein structure plays a quintessential role in the development of our understanding of evolution and the function of biological processes.

Currently protein structures are determined experimentally by x-ray crystallography and NMR spectroscopy. These methods, although accurate, are time consuming and suffer from inherent drawbacks. There is a need for the development of theoretical methods which allow for the ab-initio calculation of protein structure.

It is important that the elucidation of protein structure can be performed at the same rate as sequencing of genomes. The phenotype (product) of a gene is a protein, and the pressure of natural selection is on the phenotype and not on the DNA. In order to be able to understand the meaning of large amounts of genomic data we need to understand how proteins (enzymes etc.) create specific functional structures.

The Protein Folding Problem refers to the combinatorial problems involved in enumerating the conformations of a given Protein molecule. Cyrus Levinthal (1968) outlined this in a simple paradox: Let each amino-acid residue in a 100 residue protein have 6 possible conformations, this leads to 6^100 possible conformations available for this protein, this calculation does not include sidechain conformations which will increase the number of degrees of freedom further. The question is now how does the protein fold given this large number of possible conformations. These simple calculations urge the development of new efficient and accurate search methods.

This project attempts to address the two main problems involved in the protein folding problem. The first problem is the understanding of the energetics involved in protein folding. This is here addressed from a thermodynamic view point, developing empirical Force Fields parameterised using experimentally determined protein structures. The second problem deals with the search problem outlined in Levinthals Paradox above.

The developed search methods and force-fields are applied to simulations of fragments of proteins which are known to contain structure, independently of the rest of the structure (Early Folding Units (Wetlaufer 1973)), and to small peptide chains that have been shown by nuclear molecular resonance (NMR) have a structure in solution.

References

Cyrus Levinthal
Are there pathways in protein folding ?
J. Chim. Phys. (1968), vol 65, pp 44-45

D.B. Wetlaufer
Nucleation, Rapid Folding, and Globular Interchain Regions
in Proteins
Proc. Natl. Acad. Sci. (1973), vol 70, pp 697-701

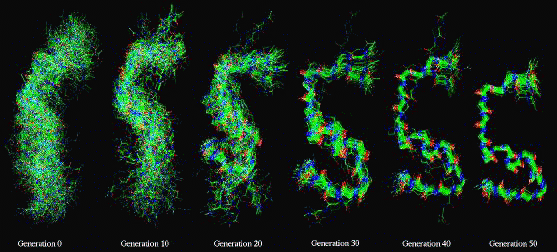
Figure 1
An illustration of Genetic Algorithm (GA) simulation of a small 22 Amino Acid peptide corresponding to the membrane binding domain of Blood Coagulation Factor VIII. The simulation attempts to select the most likely conformation of the peptide using an objective energy function which describes the mechanics of the peptide chain. The Genetic Algorithm emulates the process of natural selection in order to search the energy space efficiently. This is illustrated in the figure by a set of snapshots taken during a 50 generation simulation, it is seen how, gradually, one conformation is selected above the others through cross-overs and recombination of fragments within the population of structures. The GA search method is able to exploit parallel computing resources to the full. The above simulation is performed using the 19 node IBM SP2 at NIST. A PostScript version is available.

Figure 2
Structure of Blood Coagulation Factor VIII membrane binding domain. The structure is the best obtained in a series of Genetic Algorithm simulations. The structure shown is similar to that obtained through nuclear molecular resonance (NMR) experiments. The peptide is shown in two representations; A) CPK illustrating the compact nature of the molecule, B) Stick rendering, showing the chemical composition of the peptide.