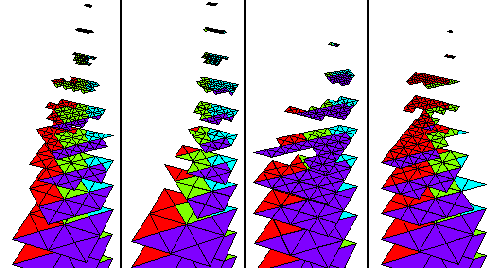
The levels of the multigrid sequence of grids on each of 4 processors.

The full domain partition provides a means of adapting the hierarchical basis multigrid method for parallel computation. Since each processor has a compatible, hierarchical adaptive grid that covers the whole domain, the multigrid algorithm can be run on each processor in parallel. Obviously, some level of communication is necessary, since the individual grids do not contain sufficient resolution over the entire domain. These communication steps occur only twice per multigrid cycle. During the fine-to-coarse half of the V-cycle the changes to the right hand side are accumulated. The first communication occurs when the coarsest grid is reached. The changes to the right hand side and current solution value are passed to all shadow copies on other processors. The second half of the V-cycle is then performed. When relaxation on the finest grid is completed, the second communication occurs; this time only the solution is passed.
The computational results of the parallel algorithm are not exactly the same as those of the sequential algorithm, because the contribution of other processors to the change in the right hand side do not arrive until the middle of the cycle. During the first half of the cycle the values from other processors are generally from the previous cycle and thus not quite correct. However, only a small part of the change comes from other processors, so this has only a small effect on the rate of convergence of the multigrid method. The following table shows the contraction factor of one V-cycle for Laplace's equation on an h-adaptive grid of linear elements with 60,000 unknowns using from 1 to 64 processors.
| Processors | 1 | 2 | 4 | 8 | 16 | 32 | 64 |
| Contraction factor | .093 | .093 | .094 | .099 | .098 | .101 | .098 |
Publications
Mitchell, W.F., Parallel Adaptive Multilevel Methods with Full Domain Partitions , App. Num. Anal. and Comp. Math., 1, (2004), pp. 36-48. ( gzipped postscript, 286k)
Mitchell, W.F., Adaptive Grid Refinement and Multigrid on Cluster Computers, Proceedings of the 15th International Parallel and Distributed Processing Symposium, IEEE Computer Society Press, 2001. ( gzipped postscript, 200k)
Mitchell, W.F., A Parallel Multigrid Method Using the Full Domain Partition, Electronic Transactions on Numerical Analysis, 6 (1998) pp. 224-233, special issue for proceedings of the 8th Copper Mountain Conference on Multigrid Methods. ( gzipped postscript, 100k)
Mitchell, W.F., The Full Domain Partition Approach for Parallel Multigrid on Adaptive Grids, Proceedings of the Eighth SIAM Conference on Parallel Processing for Scientific Computing, 1997. (gzipped postscript, 179k)
Last change to this page: December 14, 2011 Date this page created: April 2, 2007 Home Page