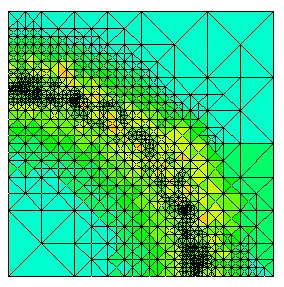
hp-adaptive grid for a circular wave front. Colors indicate the degree of the elements, with blue being low degree and red being high degree.

PHAML supports 5 types of grid refinement:
h-refinement is accomplished using newest node bisection of triangles. To refine a triangle, one of the vertices, called the peak, is connected to the midpoint of the opposite side, called the base. The new vertex becomes the peak of the new triangles. Unlike other adaptive refinement strategies, newest node bisection always maintains a compatible grid with no hanging nodes. This is accomplished by always refining triangles in pairs (except when the base is on the boundary). If two triangles share a common base, they can be refined as a pair. If not, then after refining one of them, one of its children will share the base of the other and they can be refined as a pair. Nondegeneracy of the triangles is guaranteed, since newest node bisection creates only 4 triangle shapes from a starting triangle. The linear h-hierarchical basis functions are easily defined by defining a new basis function at the new vertex while leaving all other basis functions unchanged. High order h-hierarchical bases are also easily defined, if the polynomial degree is constant throughout the grid.
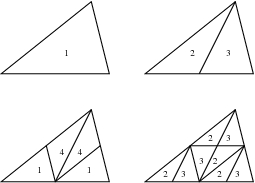
Peaks must be assigned to the initial grid in such a way that every triangle is paired with another triangle, or the boundary. It has been proven that such a perfect matching exists for any compatible triangulation, but finding it is, in general, an NP-hard problem. But given any initial triangulation, a triangulation can be constructed for which the matching is trivial. This is accomplished by pairing up as many triangles as possible with a simple algorithm, bisecting these pairs of triangles, and trisecting any remaining triangles by connecting the midpoint of the triangle to the three vertices. The vertices created by this process are the peaks of the triangles in the new initial grid.
p-refinement means to increase the degree of the piecewise polynomials over a triangle. The p-hierarchical basis functions consist of a linear basis function associated with each vertex, quadratic and higher bases associated with each edge, and cubic and higher bases associated with each triangle. In PHAML, the degree of two neighboring triangles is restricted to differ by at most 1. The degree of the edge between two triangles is the maximum of the degrees of the two triangles.
hp-adaptive refinement uses both h- and p-refinement. The advantage is that it can achieve exponential rates of convergence w.r.t. the number of degrees of freedom. We have implemented 13 strategies for hp-adaptive refinement in PHAML and used it to perform an experiment to compare the effectiveness of these strategies using 21 test problems.
Publications
Mitchell, W.F. and McClain, M.A., A Comparison of hp-Adaptive Strategies for Elliptic Partial Differential Equations, ACM Transactions on Mathematical Software , 41 (1), 2014. (preprint, pdf, 792K) ( link to journal) DOI 10.1145/2629459
Mitchell, W.F. and McClain, M.A., A Comparison of hp-Adaptive Strategies for Elliptic Partial Differential Equations (long version), NISTIR 7824, 2011. ( pdf, 33M, 215 pages)
Mitchell, W.F., A Collection of 2D Elliptic Problems for Testing Adaptive Algorithms, NISTIR 7668, 2010. ( pdf, 1.6M)
Mitchell, W.F. and McClain, M.A., A Survey of hp-Adaptive Strategies for Elliptic Partial Differential Equations, in Recent Advances in Computational and Applied Mathematics (T. E. Simos, ed.), Springer, 2011, pp. 227-258. (preprint, pdf, 16M)
Mitchell, W.F., Adaptive refinement for arbitrary finite element spaces with hierarchical bases, J. Comp. Appl. Math. 36 (1991), pp. 65-78.
Mitchell, W.F. A comparison of adaptive refinement techniques for elliptic problems. ACM Trans. Math. Soft. 15 (1989), pp. 326-347.
Mitchell, W.F., Unified multilevel adaptive finite element methods for elliptic problems, Ph.D. thesis, Technical report UIUCDCS-R-88-1436, Department of Computer Science, University of Illinois, Urbana, IL, 1988. ( gzipped postscript, 194k)
Last change to this page: December 14, 2011 Date this page created: April 2, 2007 Home Page