Oxs Extension Module: CED_UniaxialAnisotropy

Description:

This is a generic Oxs extension object, derived from the Oxs_Energy class. It provides uniaxial anisotropy with second (K1) and fourth (K2) order terms. In the easy axis case (K1>0) the energy density E is computed by

E = K₁|u×m|² + K₂|u×m|⁴,

where m is the reduced (unit) magnetization and u is the easy axis. Here the energy is zero if the magnetization is aligned with the easy axis.

In hard axis case (K1<0) the energy is offset so that the zero point occurs when the magnetization lies in the easy plane (i.e., orthogonal to the hard axis). In this case the energy density is given by

E = -K₁(u·m)² - K₂(u·m)⁴.

Either way, the field H is computed via the relation

µ₀M_sH = 2K₁(u·m)u + 4K₂(u·m)³u,

where M_s is the saturation magnetization.

This class was written and contributed by Jürgen Zimmermann, Richard Boardman and Hans Fangohr of the Computational Engineering and Design Group, University of Southampton.

Installation:

Download the header and source code files below, and follow the general Oxs extension installation instructions.

Usage:

MIF 2.x files written to use this class should include a Specify block of the form

Specify CED_UniaxialAnisotropy:name {
K1 k1_value
K2 k2_value
axis anisotropy_axis
}

The values for the K1 and K2 parameters should be scalar field objects, and axis should be a vector field object. The only difference with respect to the stock Oxs_UniaxialAnisotropy class is the inclusion of the K2 term.

Details:

Authors: Jürgen Zimmermann, Richard Boardman, and Hans Fangohr
Affiliation: Computational Engineering and Design Group, University of Southampton
Oxs_Ext class: CED_UniaxialAnisotropy
OOMMF releases: 1.2a3
External libraries: none
License: Public Domain
Release date: 7-July-2004

Download:

C++ header file: ced_uniaxialanisotropy.h
C++ main source file: ced_uniaxialanisotropy.cc
Example MIF input files:
- K2 = 0.0 K1: quadrupole00pc.mif
- K2 = 0.1 K1: quadrupole10pc.mif
- K2 = 0.3 K1: quadrupole30pc.mif

Sample results:

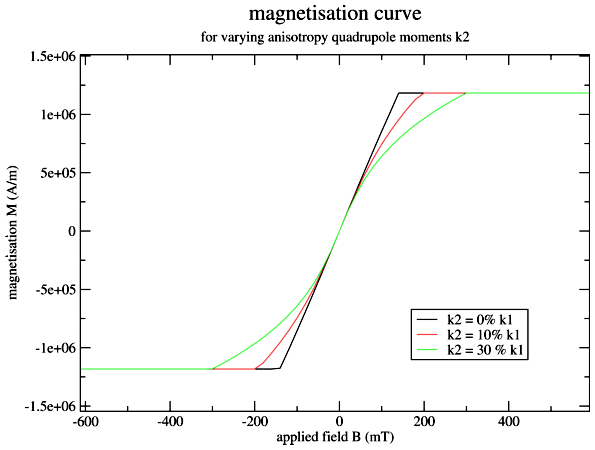
Output from the three example MIF files, illustrating the effect of increasing K2 relative to K1:

DISCLAIMER: This software was not developed at and is not supported by the National Institute of Standards and Technology. NIST assumes no responsibility whatsoever for its use, and makes no guarantees, expressed or implied, about its quality, reliability, or any other characteristic.

Back to Oxs extensions, or

This page maintained by [email protected]
27-Nov-2006