Press
here
to get the full document in PostScript format.
Press
here
to get this subdocument in PostScript format.
Numerical Evaluation of Special Functions
D. W. Lozier and F. W. J. Olver
5.8. Legendre and Associated Legendre Functions
.
This section includes the conical and toroidal functions.
See also hypergeometric functions (§ 5.5) and orthogonal
polynomials (§ 5.10).
5.8.1. Real Argument and Parameters.
Software Packages:
[ Bra73, Fortran]
,
[ Del79, Fortran]
,
[ Gau65, Algol]
,
[ LS81, Fortran]
,
[ OS83, Fortran]
.
Intermediate Libraries:
[ Bak92]
.
Comprehensive Libraries:
Numerical Recipes,
SLATEC.
5.8.2. Complex Argument and/or Parameters.
Algorithms:
[ Kol81, conical with real argument]
.
Intermediate Libraries:
[ Bak92]
.
Interactive Systems:
Mathematica.
5.8.3. Articles.
[ CM78]
,
[ CM79]
,
[ EWB84]
,
[ Fet70]
,
[ SOL81]
.
References
- Bak92
-
L. Baker, C mathematical function handbook, McGraw-Hill, Inc., New
York, 1992, includes diskette.
- Bra73
-
W. J. Braithwaite, Associated Legendre polynomials, ordinary and
modified spherical harmonics, Comput. Phys. Comm. 5 (1973), 390--394.
- CM78
-
J. N. L. Connor and D. C. Mackay, Accelerating the convergence of the
zonal harmonic series representation in the Schumann resonance problem, J.
Atmospheric Terrestrial Phys. 40 (1978), 977--980.
- CM79
-
J. N. L. Connor and D. C. Mackay, Calculation of angular distributions in
complex angular momentum theories of elastic scattering, Molecular Phys.
37 (1979), 1703--1712.
- Del79
-
G. Delic, Chebyshev expansion of the associated Legendre polynomial
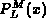 , Comput. Phys. Comm. 18 (1979), 63--71.
, Comput. Phys. Comm. 18 (1979), 63--71.
- EWB84
-
A. S. Elder, J. N. Walbert, and E. C. Benck, Calculation of Legendre
functions on the cut for integral order and complex degree by means of
Gauss continued fractions, Tech. Report ARBRL--MR--03335, U. S. Army
Armament Research and Development Center, Ballistic Research Laboratory,
Aberdeen Proving Ground, Maryland, 1984, copies obtainable from National
Technical Information Service, U. S. Dept. of Commerce, Springfield, VA
22161.
- Fet70
-
H. E. Fettis, A new method for computing toroidal harmonics, Math. Comp.
24 (1970), 667--670.
- Gau65
-
W. Gautschi, Algorithm 259. Legendre functions for arguments larger than
one, Comm. ACM 8 (1965), 488--492, for remark see ACM Trans. Math.
Software, v. 3 (1977), pp. 204-205.
- Köl81
-
K. S. Kölbig, A program for computing the conical functions of the
first kind
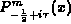 for m = 0 and m=1, Comput.
Phys. Comm. 23 (1981), 51--61.
for m = 0 and m=1, Comput.
Phys. Comm. 23 (1981), 51--61.
- LS81
-
D. W. Lozier and J. M. Smith, Algorithm 567. Extended-range arithmetic
and normalized Legendre polynomials, ACM Trans. Math. Software 7
(1981), 141--146.
- OS83
-
F. W. J. Olver and J. M. Smith, Associated Legendre functions on the
cut, J. Comput. Phys. 51 (1983), 502--518.
- SOL81
-
J. M. Smith, F. W. J. Olver, and D. W. Lozier, Extended-range arithmetic
and normalized Legendre polynomials, ACM Trans. Math. Software 7
(1981), 93--105.
Abstract:
This document is an excerpt from the current hypertext version of
an article that appeared in Walter Gautschi (ed.),
Mathematics of Computation 1943--1993: A Half-Century of
Computational Mathematics, Proceedings of Symposia in
Applied Mathematics 48, American Mathematical Society,
Providence, RI 02940, 1994.
The symposium was held at the University of British Columbia
August 9--13, 1993, in honor of the fiftieth anniversary of
the journal Mathematics of Computation.
The original abstract follows.
Higher transcendental functions continue to play varied and
important roles in investigations by engineers, mathematicians,
scientists and statisticians.
The purpose of this paper is to assist in locating useful approximations
and software for the numerical generation of these functions, and to
offer some suggestions for future developments in this field.
Applied and Computational Mathematics Division,
National Institute of Standards and Technology,
Gaithersburg, Md 20899
E-mail address: dlozier@nist.gov
Institute for Physical Science and Technology,
University of Maryland,
College Park, MD 20742
E-mail address: olver@bessel.umd.edu
The research of the second author has been supported by NSF
Grant CCR 89-14933.
1991 Mathematics Subject Classification. Primary 65D20;
Secondary 33-00.
Daniel W Lozier
Fri Apr 7 14:18:05 EDT 1995
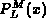 , Comput. Phys. Comm. 18 (1979), 63--71.
, Comput. Phys. Comm. 18 (1979), 63--71.
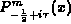 for m = 0 and m=1, Comput.
Phys. Comm. 23 (1981), 51--61.
for m = 0 and m=1, Comput.
Phys. Comm. 23 (1981), 51--61.
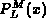 , Comput. Phys. Comm. 18 (1979), 63--71.
, Comput. Phys. Comm. 18 (1979), 63--71.
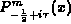 for m = 0 and m=1, Comput.
Phys. Comm. 23 (1981), 51--61.
for m = 0 and m=1, Comput.
Phys. Comm. 23 (1981), 51--61.