Mathematics of the Finite Element Method

Why the Finite Element Method?

Finite element method provides a greater flexibility to model complex geometries than finite difference and finite volume methods do. It has been widely used in solving structural, mechanical, heat transfer, and fluid dynamics problems as well as problems of other disciplines.

The advancement in computer technology enables us to solve even larger system of equations, to formulate and assemble the discrete approximation, and to display the results quickly and convienently. This has also helped the finite element method become a powerful tool.

Objective

The objective of this course is to introduce the finite element method using ANSYS and FLOTRAN and their procedures. At the completion of this course, students should be able to start using these packages and continue to develop their proficiencies.

Contents

This course will cover the following topics:

• Mathematics of Finite element method
• Getting started using ANSYS
• Building the model
• Loading and solution
• Reviewing results
• FLOTRAN Procedures

References

1. Strang, G. and Fix, G. J., An Analysis of the Finite Element Method. Prentice-Hall, Inc., 1973.
2. Strang, G., Introduction to Applied Mathematics. Wellesley-Cambridge Press, 1986.
3. Swanson Analysis Systems, Inc., Ansys User's Manual for Revision 5.0} Swanson Analysis Systems, Inc., 1992.
4. Swanson Analysis Systems, Inc. Flotran User's Manual for Revision 2.1A Swanson Analysis Systems, Inc., 1992.

Mathematics of Finite Element Method

Consider a second order differential equation in one dimension:

with boundary conditions specified at x=0 and x= .

This is the Sturm-Liouville equation that can be used to represent a variety of physical processes:

• Heat conduction along a rod
• Shaft torsion
• Displacement of a rotating string
• Deflection on an elastic beam

In three dimensional space, this equation becomes an elliptic boundary value problem, such as a 3-D elasticity problem and the LaPlace/Poisson equation.

Let's generalize the differential equation as the following:

where L is a linear operator.

Let ( , ) stand for the dot product of two vectors and define:

Then has a minimum at

Thus gives a minimum .

If has a minimum at , then for all and ,

Since can be arbitrary small and of either sign, its coefficient,, must vanish. Therefore,

for all

This is the basis of the finite element analysis method. We solve instead of .

is called the weak form or the Galerkin form. It no longer requires to be positive definite, or even symmetric, since it deals only with a stationary point, such as a saddle point, which is not necessarily a minmum.

It is worth noting that the least-square function,

has its minimum (zero) at the same point that satisfies . However, it is actually , instead of . As long as L is inversible, the two equations are equivalent.

In the finite element analysis method, we solve instead of .

Now consider the one dimensional equation again with very fine elements. The inner product of two vectors is analogous to the integration over the interval, .

Therefore,

Compute using integration by part:

and

Similarily in three dimensional space,

and

FEM Applications

In practice, the finite element method has been used to solve second order partial differential equations. We will concentrate on three classes of problems:

1. Engineering mechanics equation,

2. The LaPlace/Poisson equation,

3. The generalized fluid transport equation,

1. Engineering mechanics equation:

Where:

• M = mass
• C = damping
• K = stiffness
• u = displacement
• F = applied load

ANSYS has the following types of analysis:

• Static ( or steady-state)
• Transient
• Harmonic
• Modal
• Spectrum
• Etc.

2. The LaPlace/Poisson equation:

• Heat conduction
• Shaft Torsion
• Flow through porous media
• Pressurized membranes
• Circulation of fluid flow
• Ideal fluid flow
• Electrostatic field
• Diffusion

Where:

• = thermal conductivity
• T = temperature
• q = internal heat generation rate

Where:

• G = shear modulus of elasticity
• = twist per unit length
• = stress function defined by:
  

Where:

• = permeability coefficient
• H = fluid head
• Q = internal flow injection rate

Where:

• T = membrane tension
• h = membrane displacement
• p = pressure imbalance

Where:

• = stream function defined by:
  

  u =       v = -  

• = vorticity

Where:

• = potential function defined by:
  

  u = -    v = -  

• = stream function defined by:
  

  u =      v = -  

Where:

• = permittivity
• V = electric potential (voltage)
• = charge density

Where:

• D = diffusion constant
• c = moisture concentration
• Q = production rate

3. The generalized fluid transport equation:

This equation represents fluid flow equations:

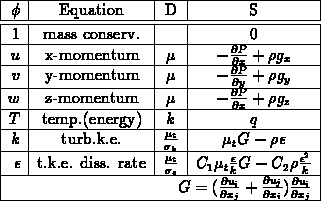
Where:

• P = pressure
• V = velocity vector
• Q = heat source
• = vorticity
• = density
• = ambient density
• = kinematic viscosity
• = heat conductivity
• = ratio of specific heat

Finite Element Discretization

Let's use the Poisson equation to illustrate the finite element discretization method:

Rewrite the equation in Cartesian Coordinates:

Remember that, in finite element method, we solve instead of ; thus we are solving,

and using integration by part, above equation becomes:

The integration over the interior surface area on an element is canceled by the integration on the neighboring element. The integration over the external surface is the known boundary condition and can be moved to the right-hand side of the equation.

Galerkin chose a finite set of functions and approximated u with , where are the u values at nodes , respectively. Substituting and into above equation, we have,

Define,

Then the equation becomes a system of linear equations,

Galerkin's approximation, , reduces to at node . This requires at node and at all other nodes. For simplicity, consider a one-dimensional linear element:

Thus is the "hat function",

Similarily for a bilinear rectangular element,

We can see that, , as long as and are not on the same element. Actual assembly of the system of equations is carried out one element at a time. The integrations over each element are approximated by a single value in a linear element or by the average over the Gauss points in a quadratic element.

Finite Element Solution

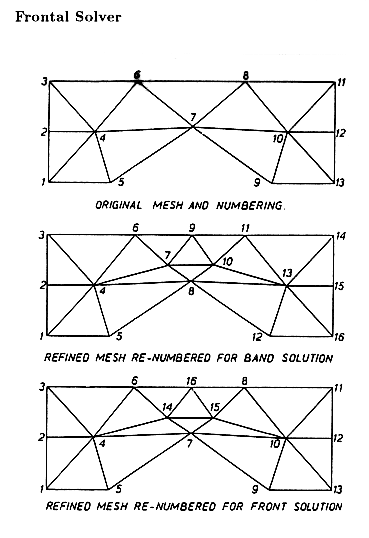
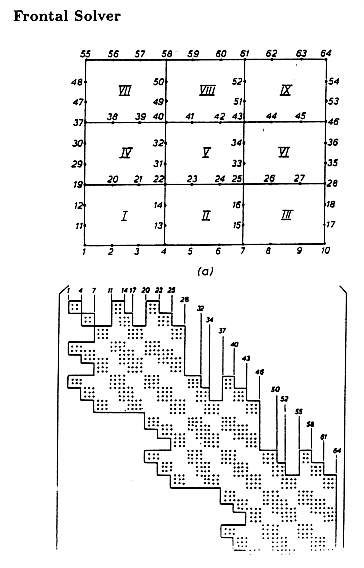
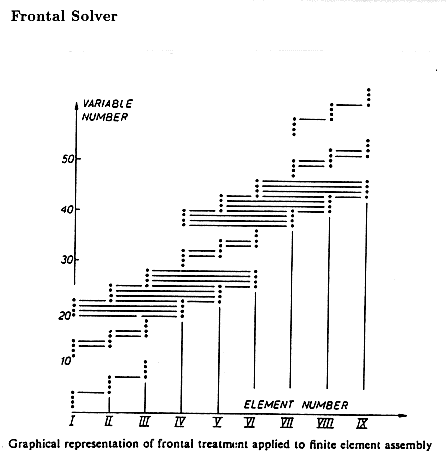
The differential equation is discretized into a series of finite element equations that form a system of equations to be solved.

Where:

• K = stiffness matrix
• u = nodal displacement vector
• F = applied load vector

Features of the Matrix

• Symmetric positive-definite
• Band matrix
• Large matrix, commonly in thousands

ANSYS has two methods of solving a large system of equations:

• Frontal solver
• Conjugate gradient solver

FLOTRAN uses iteration methods solving individual variables sequentially:

• Tri-diagonal matrix method
• Conjugate gradient method

Frontal Solver

• Computations in the sequence of elements
• Assembly-elimination process of variables (nodes) - analogous to the paging of a virtual memory operating system to keep memory requirement minimum. Variables that are needed for computation are loaded into memory, and variables that are no longer neededi are eliminated, moved to the virtual space, or written to files so that the memory requirement is kept to a minimum.
• This minimum memory is called the wavefront limit.

Conjugate Gradient Solver

Solve Ax=b

This is equivalent to find x to minimize

Given a guess , not a solution,

set

set

where minimizes E() for all vectors of the form

This is the steepest descent. Unfortunately its convergence can be very slow. This leads to a conjugate gradient solver:

Given a guess , compute , and set the initial descent direction to the

Compute a new descent direction A-orthogonal to all of its predecessors

The conjugate gradient solver often gives satisfactory accuracy after only a very few iterations.