Finite element method provides a greater flexibility to model complex geometries than finite difference and finite volume methods do. It has been widely used in solving structural, mechanical, heat transfer, and fluid dynamics problems as well as problems of other disciplines.
The advancement in computer technology enables us to solve even larger system of equations, to formulate and assemble the discrete approximation, and to display the results quickly and convienently. This has also helped the finite element method become a powerful tool.
The objective of this course is to introduce the finite element method using ANSYS and FLOTRAN and their procedures. At the completion of this course, students should be able to start using these packages and continue to develop their proficiencies.
This course will cover the following topics:
Consider a second order differential equation in one dimension:
with boundary conditions specified at x=0 and x= .
This is the Sturm-Liouville equation that can be used to represent a variety of physical processes:
In three dimensional space, this equation becomes an elliptic boundary value problem, such as a 3-D elasticity problem and the LaPlace/Poisson equation.
Let's generalize the differential equation as the following:
where L is a linear operator.
Let ( , ) stand for the dot product of two vectors and define:
Then has a minimum at
Thus gives a minimum
.
If has a minimum at
, then for all
and
,
Since can be arbitrary small and of either sign,
its coefficient,
, must vanish.
Therefore,
for all
This is the basis of the finite element analysis method.
We solve instead of
.
is called the weak form or the
Galerkin form. It no longer requires
to be positive
definite, or even symmetric, since it deals only with a
stationary point, such as a saddle point, which is not necessarily
a minmum.
It is worth noting that the least-square function,
has its minimum (zero) at the same point that satisfies
. However, it is actually
,
instead of
. As long as L is inversible, the
two equations are equivalent.
In the finite element analysis method, we solve
instead of
.
Now consider the one dimensional equation again with very fine
elements. The inner product of two vectors is analogous to the
integration over the interval, .
Therefore,
Compute using integration by part:
and
Similarily in three dimensional space,
and
In practice, the finite element method has been used to solve second order partial differential equations. We will concentrate on three classes of problems:
1. Engineering mechanics equation,
2. The LaPlace/Poisson equation,
3. The generalized fluid transport equation,
Where:
ANSYS has the following types of analysis:
Where:
Where:
Where:
Where:
Where:
u =v = -
Where:
u = -v = -
u =v = -
Where:
Where:
This equation represents fluid flow equations:
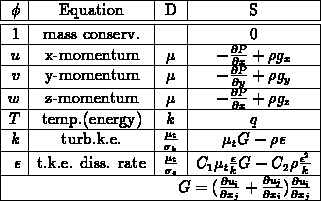
Where:
Let's use the Poisson equation to illustrate the finite element discretization method:
Rewrite the equation in Cartesian Coordinates:
Remember that, in finite element method, we solve instead of
; thus we are solving,
and using integration by part, above equation becomes:
The integration over the interior surface area on an element is
canceled by the integration on the neighboring element. The
integration over the external surface is the known boundary
condition and can be moved to the right-hand side of the
equation.
Galerkin chose a finite set of functions
and approximated u with
, where
are the u values at
nodes
, respectively. Substituting
and
into
above equation, we have,
Define,
Then the equation becomes a system of linear equations,
Galerkin's approximation, ,
reduces to
at node
. This requires
at node
and
at all other nodes. For simplicity, consider a
one-dimensional linear element:
Thus is the "hat function",
Similarily for a bilinear rectangular element,
We can see that, , as long as
and
are not on
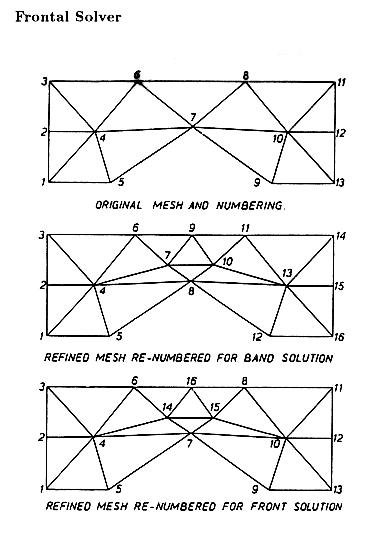
the same element. Actual assembly of the system of equations is
carried out one element at a time. The integrations over each
element are approximated by a single value in a linear element
or by the average over the Gauss points in a quadratic element.
The differential equation is discretized into a series of finite element equations that form a system of equations to be solved.
Where:
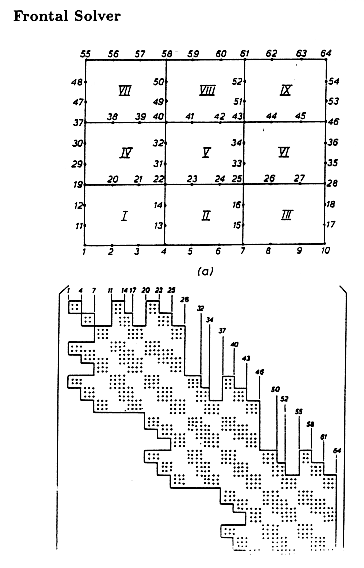
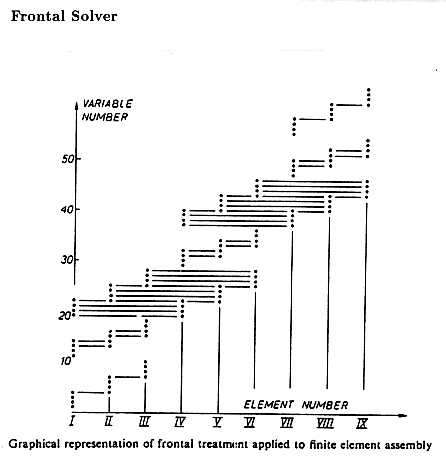
Features of the Matrix
ANSYS has two methods of solving a large system of equations:
FLOTRAN uses iteration methods solving individual variables sequentially:
Solve Ax=b
This is equivalent to find x to minimize
Given a guess , not a solution,
set
set
where minimizes E(
) for all vectors of the form
This is the steepest descent. Unfortunately its convergence can be very slow. This leads to a conjugate gradient solver:
Given a guess , compute
, and
set the initial descent direction
to the
Compute a new descent direction A-orthogonal to all of its predecessors
The conjugate gradient solver often gives satisfactory accuracy after only a very few iterations.