In a word, yes. But the elasticity is a way to characterize the mechanical response of the material body for applied stresses that stay within the linear regime. Very large stresses, which are high enough to fracture the material, cause non-linear deformations. These values vary greatly depending on the overall makeup of the concrete mixture. Many of the non-fracture-related mechanical properties of concrete are characterized by the elastic moduli. For example, in many buildings the stiffness of the structure, made up of reinforced-steel concrete beams, is more important than the strength of the structure. The stiffness of the structure is directly related to the stiffness of the concrete, which is a function of its elastic moduli.

The elastic moduli prediction code is set up to compute the elastic moduli of an arbitrary material. As long as the microstructure can be represented by a 3-D digital image, and the individual phase elastic moduli are known, the program can be used to compute the overall moduli. The overall elastic moduli are functions of the microstructure as well as of the elastic moduli of the individual chemical phases in the cement paste. These can be as many as 20 or 30, since cement paste by itself is a chemically complex material.

The elastic moduli prediction code has been parallelized.

	Why Parallelize these Calculations? Part of the intrinsic error that comes about with the use of 3-D digital images to represent microstructure is digital resolution error. This can be quantified and eliminated by investigating the same problem at several resolutions, looking at large enough systems to see the asymptotic behavior. The parallel implementation of the elastic code enables this to be easily and more accurately done.
	How is the Parallelization Realized? The parallelization was created using MPI and FORTRAN90 for a distributed memory machine, ie. a PC-cluster running Linux. This new code contains 3 predominant features which increase the speed and allow the user to handle much larger problem sizes. Removal of ib array: This array is a hash table which needs requires 27 times the memory the size of the data set. The new parallel code allows one to address the needed array elements directly by virtue of storing them in the "natural" 3-dimensional (x,y,z) manner which mimics the spatial geometry of the actual sample. 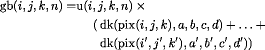Calculation of gb and Ah arrays: These calculations consume over 90% of runtime due to the complexity of statements, viz: These calculations are now in the form of: The removal of the ib array allows the computer to increase its access speed to the desired dk array elements by removing a degree of indexing. Increasing problem size/decreasing overall runtime: On a single processor the entire data array must be loaded. However, the use of parallel programming allows one to use approximately 1/nth the amount of memory per processing node or allows one to run a problem that is essentially N times larger overall.
	What is the Performance of the Parallel Code? The time required to run a 300^3 (27 million voxels) job using the serial version is nominally 120 hours. This new code is able run the same calculation on 8 CPUs on an SGI Origin 2000 in about 6.42 hours; a speed-up of 18.69.

Besides some work on cement paste, the serial code has already been applied to porous ceramics, porous glasses, rocks, open and closed cell foams, and metal matrix composites. This parallel code will allow calculations on much larger systems in a timely way, on the order of 300-600^3 voxels in size, will allow many more applications and not only to concrete. One important application is to quantify 3-D microstructure using x-ray tomography. Various codes are then applied to the resulting 3-D structure to compute various quantities. These data sets are typically of size 512^3 or greater. In the past, a piece had to be digitally cut out of the data set in order to be able to compute quantities like elastic moduli, which induces finite size error. Now such large data sets can be routinely processed with the parallel elastic moduli code.

There also many problems that are not large in spatial size, but require better digital resolution. One example is the early age elastic properties of cement paste. To properly resolve the small necks of material that are holding the solid backbone together requires a fine digital resolution. The parallel code makes such fine resolution possible.